Оптимизация как путь к катастрофеПростейшая модель роста
Ясно, что общество (во всех странах) не может этого допустить, и следовательно развитие науки должно быть подавлено (что мы и наблюдаем во многих странах; в России реформирование академической науки происходит как раз сейчас). Аналогичные явления насыщения происходят в любой популяции (и, вероятно, вскоре произойдут с человечеством в целом): когда население становится слишком большим, мальтусовская жесткая модель с постоянным коэффициентом роста k перестает быть применимой. Естественно, при слишком больших x конкуренция за ресурсы (пищу, гранты и т. д.) приводит к уменьшению k, и жесткая модель Мальтуса должна быть заменена мягкой моделью
На рис. 5 слева изображен график функции k(x)x, положительной между точками A и B. В центре изображено векторное поле 1 на изображающей всевозможные состояния системы оси x. Оно указывает скорость эволюции состояния. В точках A и B скорость равна нулю: это стационарные состояния. Между A и B скорость положительна (население растет), а за точкой B -- отрицательна (население убывает). Справа изображена результирующая зависимость населения от времени при разных начальных условиях. Модель предсказывает, что с течением времени устанавливается стационарный режим B, который устойчив: большее население уменьшается, меньшее -- увеличивается. Логистическая модель удовлетворительно описывает многочисленные явления насыщения. Вблизи A, когда население мало, она очень близка к мальтузианской модели. Но при достаточно больших x (порядка 1/2 при нашем выборе коэффициентов) наблюдается резкое отличие от мальтузианского роста (обозначенного на рис. 5 пунктиром): вместо ухода x на бесконечность население приближается к стационарному значению B. Население Земли сейчас приближается к 6 миллиардам. Стационарное значение (по разным оценкам) 16-20 миллиардов человек. Логистическая модель является обычной в экологии. Можно себе представить, например, что x -- это количество рыб в озере или в мировом океане. Посмотрим теперь, как скажется на судьбе этих рыб рыболовство с интенсивностью c:
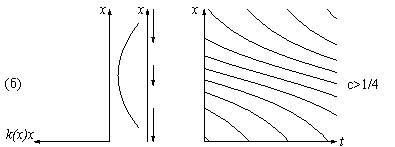
Вычисления показывают, что ответ резко меняется при некотором критическом значении квоты вылова, c. Для нашей жесткой модели это критическое значение есть c= 1/4, но аналогичные явления имеют место и для мягкой модели
(критическое значение с в этом случае максимум функции k(x)x).
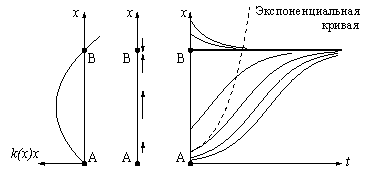
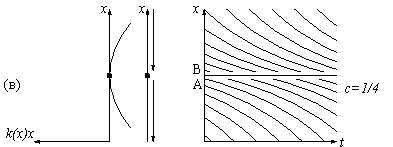
Ход эволюции числа рыб x с течением времени t изображен на рис. 6. Если квота c мала, то изменения (по сравнению со свободной популяцией, для которой c =0) состоят в следующем. Система имеет два равновесных состояния, A и B. Состояние B устойчиво: популяция в этом случае несколько меньше, чем необлавливаемая, но она восстанавливается при малых отклонениях x от равновесного значения B. Состояние A неустойчиво: если вследствие каких-либо причин (скажем, браконьерства или мора) размер популяции упадет хоть немного ниже уровня A, то в дальнейшем популяция (хотя и медленно, если отличие от A невелико) будет уничтожена полностью за конечное время. По моему мнению, состояние науки в России в настоящее время описывается примерно точкой A: оно еще стационарно, но, как говорят физики, квазистационарно в том смысле, что небольшое встряхивание может легко привести к необратимому уничтожению. При бoльших критической квотах вылова c популяция x уничтожается за конечное время, как бы велика она ни была в начальный момент. Это -- судьба мамонтов, бизонов, многих китов: экологи подсчитали, сколько видов погибает ежедневно под влиянием деятельности человека, и эти цифры ужасают. Модели этого рода описывают также банкротство фирм, концернов и государств. Опасность уничтожения в нашей модели появляется тогда, когда неустойчивое состояние A приближается к устойчивому состоянию B, т. е. когда величина x опускается примерно до половины исходной стационарной величины необлавливаемой популяции. Население России, мне кажется, еще не понизилось до этого смертельно опасного уровня, но, по-видимому, движется к нему. Наука же в России находится в настоящее время именно в таких условиях "перелова". Например, заработная плата главного научного сотрудника в Математическом институте им. Стеклова РАН (каковым я являюсь) составляет менее 100 долларов в месяц. Это раз в сто меньше зарплаты моих коллег в США (и раз в 50 меньше, чем во Франции). Понятно, что в таких условиях величина c (скорость убыли числа ученых в России) ограничивается в основном дискриминационными мерами, принимаемыми Западом (например, США) для охраны своих рабочих мест от наплыва лучше подготовленных иностранных аспирантов и докторантов (в основном из Китая и из России). Из сказанного видно, что выбор значения параметра c является чрезвычайно важным моментом управления эксплуатацией популяции x. Стремясь к увеличению квоты эксплуатации c, разумная планирующая организация не должна превосходить критический уровень (в нашем случае c�1/4). Оптимизация приводит к выбору именно критического значения c= 1/4, при котором эксплуатируемая популяция еще не уничтожается, но доход от эксплуатации за единицу времени достигает максимально возможного значения c = 1/4 (больший доход в нашей популяции в течение длительного времени невозможен, так как максимальная скорость прироста даже и неэксплуатируемой популяции есть 1/4). Из нижней части рис. 6 мы видим, что произойдет при таком "оптимальном" выборе, c= 1/4. Какова бы ни была начальная популяция x > 1/2, с течением времени она выйдет на стационарный режим A=B = 1/2. Эта стационарная популяция, однако, неустойчива. Небольшое случайное уменьшение x приводит к полному уничтожению популяции за конечное время. Следовательно, оптимизация параметров плана может приводить (и приводит во многих случаях, из которых наша модель -- лишь простейший пример) к полному уничтожению планируемой системы вследствие возникающей из-за оптимизации неустойчивости. Наша мягкая модель, при всей своей очевидной примитивности, позволяет, однако, предъявить способ борьбы с указанным злом. Оказывается, устойчивость восстанавливается, если заменить жесткое планирование обратной связью. Иными словами, решение о величине эксплуатации (квоты вылова, налогового пресса и т. д.) следует принимать не директивно (c=const), а в зависимости от достигнутого состояния системы: c=kx,
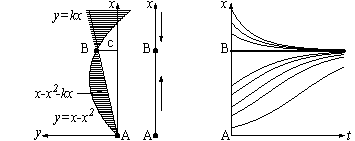
В этом случае модель принимает вид (рис. 7)
Более того, небольшое отклонение коэффициента от оптимального значения k= 1/2 приводит не к самоуничтожению системы (как это было при небольшом отклонении от оптимального жесткого плана c), а лишь к небольшому уменьшению "дохода". Итак, введение обратной связи (т. е. зависимости принимаемых решений от реального состояния дел, а не только от планов) стабилизирует систему, которая без обратной связи разрушилась бы при оптимизации параметров. Все сказанное выше останется справедливым и для мягкой модели (с соответствующим пересчетом коэффициентов). Следует подчеркнуть, что именно эта независимость от деталей жесткой модели (которые, как правило, не слишком хорошо известны) делает выводы мягкого моделирования полезными. Попытки заменить мягкое моделирование жестким обычно приводят к иерархии все более сложных и громоздких математических построений, исследование которых доставляет прекрасный материал для большого количества диссертаций, но реальная ценность которых зачастую не превосходит в сущности простых (хотя без математики и не очевидных) выводов, основанных на анализе именно простейших моделей, подобных описанной выше.
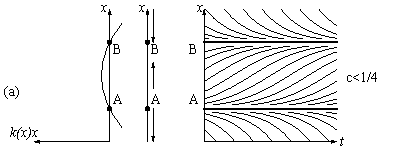
1Именно, в каждой точке, изображающей состояния, приложен вектор скорости изменения этого состояния, т. е.
|

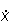 =kx предложена Мальтусом (для роста населения Земли). Она ведет, как хорошо известно, к экспоненциальному (т. е. очень быстрому) росту населения x с течением времени. Эта жесткая модель применима (разумеется, с оговорками), например, к развитию науки в 1700-1950 годах (измеряемому, скажем, числом научных статей) (рис. 4). Продолжение экспоненциального роста науки в следующий век быстро привело бы к исчерпанию бумаги и чернил, причем число ученых должно было бы достичь половины населения земного шара.
=kx предложена Мальтусом (для роста населения Земли). Она ведет, как хорошо известно, к экспоненциальному (т. е. очень быстрому) росту населения x с течением времени. Эта жесткая модель применима (разумеется, с оговорками), например, к развитию науки в 1700-1950 годах (измеряемому, скажем, числом научных статей) (рис. 4). Продолжение экспоненциального роста науки в следующий век быстро привело бы к исчерпанию бумаги и чернил, причем число ученых должно было бы достичь половины населения земного шара.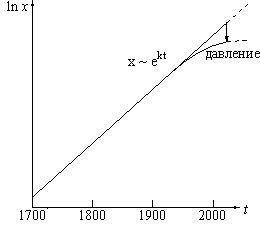
 . См, например [10], с. 32.
. См, например [10], с. 32.


