При рассмотрении радиационного теплообмена в геометрически сложных системах расчет угловых коэффициентов должен осуществлять с учетом возможного взаимного затенения участвующих в теплообмене поверхностей. Учет возможного взаимного затенения осуществляется следующим образом:
Участвующие в лучистом теплообмене поверхности исследуемого объекта как уже отмечалось выше заменяются многогранными поверхностями с треугольными гранями. Число граней (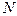 ) у той части поверхности объекта, для которой осуществляется расчет распределения локальной плотности
) у той части поверхности объекта, для которой осуществляется расчет распределения локальной плотности  падающих лучистых потоков, должно быть достаточно большим, чтобы в пределах каждой грани величину
падающих лучистых потоков, должно быть достаточно большим, чтобы в пределах каждой грани величину  можно было бы считать постоянной величиной и, кроме того, можно было бы достаточно точно учесть эффект возможного взаимного затенения. Другие поверхности объекта, которые являются потенциальными затенителями для рассматриваемой его части, могут аппроксимироваться многогранными поверхностями с небольшим числом граней. Главное, чтобы аппроксимирующая поверхность создавала такой же затеняющий эффект для рассматриваемой части объекта, как и реальная поверхность. Аппроксимацию можно осуществить, задав в какой-то удобной системе координат координаты характерных точек, которые станут вершинами треугольных граней.
можно было бы считать постоянной величиной и, кроме того, можно было бы достаточно точно учесть эффект возможного взаимного затенения. Другие поверхности объекта, которые являются потенциальными затенителями для рассматриваемой его части, могут аппроксимироваться многогранными поверхностями с небольшим числом граней. Главное, чтобы аппроксимирующая поверхность создавала такой же затеняющий эффект для рассматриваемой части объекта, как и реальная поверхность. Аппроксимацию можно осуществить, задав в какой-то удобной системе координат координаты характерных точек, которые станут вершинами треугольных граней.
Для каждой из 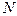 граней определяются направляющие косинусы нормалей
граней определяются направляющие косинусы нормалей  и координаты центральных точек
и координаты центральных точек 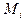 . В качестве этих точек принимаются точки пересечения медиан. Процедуры нумерации граней, определения направляющих косинусов их нормалей и определения координат центральных точек весьма упрощается, если точки на поверхности задавать в виде рядов точек с одинаковым числом в каждом ряде.
. В качестве этих точек принимаются точки пересечения медиан. Процедуры нумерации граней, определения направляющих косинусов их нормалей и определения координат центральных точек весьма упрощается, если точки на поверхности задавать в виде рядов точек с одинаковым числом в каждом ряде.
Аппроксимация поверхностей исследуемого объекта многогранными поверхностями создает предпосылки для эффективного использования при расчете угловых коэффициентов между треугольными гранями метода контурного интегрирования дифференциального углового коэффициента. К числу этих предпосылок можно отнести то, что в любом случае для других целей будут вычисляться направляющие косинусы нормалей граней, координаты вершин граней и координаты их центральных точек. При этом вычислительный алгоритм для 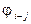 имеет весьма простой вид и его реализация требует относительно небольших затрат компьютерного времени. Допустим, например, что нормаль центральной элементарной площадки
имеет весьма простой вид и его реализация требует относительно небольших затрат компьютерного времени. Допустим, например, что нормаль центральной элементарной площадки  -ой грани имеет направляющие косинусы
-ой грани имеет направляющие косинусы  , а координатами центральной точки этой площадки являются
, а координатами центральной точки этой площадки являются 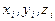 , тогда
, тогда
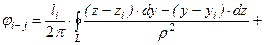
 + +
+ +  (4.1)
(4.1)
где  ,
,
 - контур
- контур 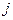 -ой грани - треугольника с известными координатами вершин;
-ой грани - треугольника с известными координатами вершин;
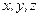 - текущие координаты контура;
- текущие координаты контура;
 - сторон треугольника.
- сторон треугольника.
Заметим, что угловой коэффициент между  -ым элементом и
-ым элементом и 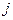 -той гранью не равен 0 только в том случае, когда косинус угла между нормалями
-той гранью не равен 0 только в том случае, когда косинус угла между нормалями  -ой и
-ой и 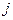 -ой граней имеет положительный знак, а также когда между этими гранями нет экранирующих поверхностей, то есть нет затенения.
-ой граней имеет положительный знак, а также когда между этими гранями нет экранирующих поверхностей, то есть нет затенения.
Однако, прежде чем воспользоваться рекомендуемым для вычисления 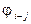 выражением, необходимо решить вопрос о наличии или отсутствии экранирования тепловоспринимающего элемента
выражением, необходимо решить вопрос о наличии или отсутствии экранирования тепловоспринимающего элемента  от излучения, исходящего от
от излучения, исходящего от 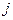 -ой грани. Если экранирование имеет место, то очевидно, что
-ой грани. Если экранирование имеет место, то очевидно, что  = 0. Если экранирование отсутствует, то
= 0. Если экранирование отсутствует, то 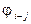 вычисляется в соответствии с приведенными выше рекомендациями. Вопрос о наличии или отсутствии экранирования решается следующим образом. Определяются точки пересечения вектора
вычисляется в соответствии с приведенными выше рекомендациями. Вопрос о наличии или отсутствии экранирования решается следующим образом. Определяются точки пересечения вектора  с плоскостями всех граней, которые могут экранировать излучение, испускаемое
с плоскостями всех граней, которые могут экранировать излучение, испускаемое 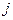 -ой гранью в направлении
-ой гранью в направлении  -ой грани. При этом вектор
-ой грани. При этом вектор  - вектор, имеющий начало в центральной точке
- вектор, имеющий начало в центральной точке  -ой грани, а конец - в центральной точке
-ой грани, а конец - в центральной точке 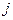 -ой грани. Если точка пересечения вектора с плоскостью грани окажется в пределах соответствующей грани, то можно сделать вывод о том, что затенение имеет место. Если точка пересечения окажется вне пределов соответствующих граней (треугольников), то это является свидетельством отсутствия затенения.
-ой грани. Если точка пересечения вектора с плоскостью грани окажется в пределах соответствующей грани, то можно сделать вывод о том, что затенение имеет место. Если точка пересечения окажется вне пределов соответствующих граней (треугольников), то это является свидетельством отсутствия затенения.
Для составления алгоритма решения задачи обнаружения взаимной затеняемости граней запишем в системе координат 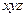 уравнение прямой, проходящей через центральные точки
уравнение прямой, проходящей через центральные точки  -ой и
-ой и 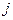 -ой граней (точки
-ой граней (точки  и
и  ). Тогда уравнение прямой, проходящей через две заданные точки
). Тогда уравнение прямой, проходящей через две заданные точки 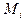 и
и 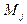 , можно записать в координатной форме:
, можно записать в координатной форме:
 , (4.2)
, (4.2)
где 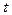 - параметр.
- параметр.
Составим теперь уравнение плоскости интересующей нас грани многогранной поверхности. Допустим, что грань ограничена точками  ,
, 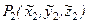 ,
,  . В этом случае уравнение плоскости, проходящей через три заданные точки, можно записать следующим образом:
. В этом случае уравнение плоскости, проходящей через три заданные точки, можно записать следующим образом:
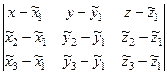 =
= 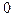 (4.3)
(4.3)
Раскрывая стоящий в левой части уравнения (4.3) определитель 3-его порядка, приведем это уравнение к общему виду, т.е. к виду

Для данного случая:
 ,
,
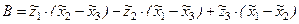 ,
,
 ,
,
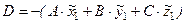 .
.
Определим координаты токи пересечения  рассматриваемых прямой и плоскости. Значение параметра
рассматриваемых прямой и плоскости. Значение параметра 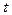 , соответствующего точке пересечения прямой и плоскости выражается через координаты точек
, соответствующего точке пересечения прямой и плоскости выражается через координаты точек 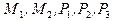 с помощью известного в курсе аналитической геометрии соотношения:
с помощью известного в курсе аналитической геометрии соотношения:
 ,
,
а координаты точки пересечения, следовательно, определяются совокупностью следующих выражений:
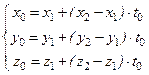
Чтобы выявить, находится ли точка пересечения  в пределах отрезка
в пределах отрезка  , сравним сумму расстояний от точки
, сравним сумму расстояний от точки  до точек
до точек 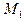 и
и  с расстоянием между точками
с расстоянием между точками  . При этом:
. При этом:
 ,
,
 ,
,
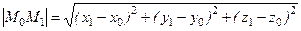 .
.
Если  , то это означает, что плоскость грани пересекается с прямой
, то это означает, что плоскость грани пересекается с прямой  за пределами отрезка
за пределами отрезка  . Затенения в этом случае нет. Если
. Затенения в этом случае нет. Если  , пересечение есть, но определенно можно говорить лишь о пересечении отрезка только с плоскостью грани.
, пересечение есть, но определенно можно говорить лишь о пересечении отрезка только с плоскостью грани.
Чтобы выяснить, находится ли точка пересечения в пределах анализируемой грани, ограниченной сторонами 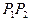 ,
, 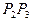 ,
,  , сопоставим площадь треугольника
, сопоставим площадь треугольника 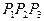
 с суммой площадей треугольников
с суммой площадей треугольников 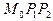 ,
,  ,
,  . В случае равенства отмеченной суммы величине площади треугольника
. В случае равенства отмеченной суммы величине площади треугольника  , можно утверждать, что точка пересечения находится в пределах рассматриваемой грани или на ее границе. Если сумма площадей окажется больше
, можно утверждать, что точка пересечения находится в пределах рассматриваемой грани или на ее границе. Если сумма площадей окажется больше 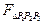 , пересечения с гранью
, пересечения с гранью 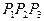 нет и, следовательно, затенения тоже нет. Что касается того случая, когда точка пересечения находится на сторонах треугольника, то он имеет место для всех граней с одной вершиной, совпадающей с центром рассматриваемого тепловоспринимающего элемента. Поэтому при реализации данной методики выявления затенения в программе для компьютера необходимо учитывать данное обстоятельство, исключая, например, из рассмотрения отмеченные грани.
нет и, следовательно, затенения тоже нет. Что касается того случая, когда точка пересечения находится на сторонах треугольника, то он имеет место для всех граней с одной вершиной, совпадающей с центром рассматриваемого тепловоспринимающего элемента. Поэтому при реализации данной методики выявления затенения в программе для компьютера необходимо учитывать данное обстоятельство, исключая, например, из рассмотрения отмеченные грани.
Величины сопоставляемых площадей можно определить, исходя из геометрического смысла векторного произведения векторов, выходящих из какой-то вершины треугольника и оканчивающихся в двух других вершинах этого треугольника, например, векторов  и
и 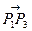 . Векторное произведение этих векторов
. Векторное произведение этих векторов 
 , как известно, можно представить в виде определителя 3-го порядка, 1-ую строку которого образуют орты
, как известно, можно представить в виде определителя 3-го порядка, 1-ую строку которого образуют орты  , а вторую и третью строки - координаты перемножаемых векторов.
, а вторую и третью строки - координаты перемножаемых векторов.

Координаты вектора, равного векторному произведению векторов, можно определить, раскрыв приведенный определитель по элементам 1-ой строки. Вычислив корень квадратный из суммы квадратов координат этого вектора, получим удвоенную площадь треугольника 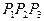 . В итоге для
. В итоге для 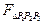 получим:
получим:


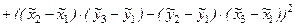
Опуская простые рассуждения и упрощающие выкладки, приведем расчетные формулы для площадей других сопоставляемых треугольников, т.е. треугольников 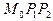 ,
,  и
и  :
:

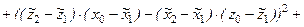
 ,
,


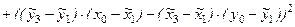 ,
,


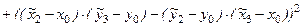 .
.
Таким образом, выявлены необходимые расчетные формулы для решения вопроса о том, затеняется или нет тот или иной тепловоспринимающий элемент другими частями его наружной поверхности от излучения, испускаемого этой поверхностью. Но прежде чем решать вопрос о затеняемости, целесообразно сначала выяснить, а может ли в силу своего расположения 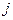 -я грань участвовать в облучении
-я грань участвовать в облучении  -ого элемента. Для этого определим косинус угла
-ого элемента. Для этого определим косинус угла  между нормалью элемента
между нормалью элемента 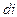
 и вектором
и вектором  , соединяющим
, соединяющим  -ый элемент с серединой
-ый элемент с серединой 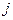 -ой грани. Если косинус угла окажется отрицательной величиной (в этом случае
-ой грани. Если косинус угла окажется отрицательной величиной (в этом случае  угол
угол  превышает
превышает 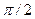 ), то грань не может участвовать в облучении
), то грань не может участвовать в облучении  -ого элемента и, следовательно, вопроса о затеняемости в этом случае не возникает,
-ого элемента и, следовательно, вопроса о затеняемости в этом случае не возникает,  поскольку
поскольку  . Косинус отмеченного угла можно определить разделив скалярное произведение векторов
. Косинус отмеченного угла можно определить разделив скалярное произведение векторов  и
и 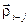 на модуль вектора
на модуль вектора  , т.е.
, т.е.  .
.

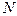 ) у той части поверхности объекта, для которой осуществляется расчет распределения локальной плотности
) у той части поверхности объекта, для которой осуществляется расчет распределения локальной плотности  падающих лучистых потоков, должно быть достаточно большим, чтобы в пределах каждой грани величину
падающих лучистых потоков, должно быть достаточно большим, чтобы в пределах каждой грани величину  и координаты центральных точек
и координаты центральных точек 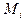 . В качестве этих точек принимаются точки пересечения медиан. Процедуры нумерации граней, определения направляющих косинусов их нормалей и определения координат центральных точек весьма упрощается, если точки на поверхности задавать в виде рядов точек с одинаковым числом в каждом ряде.
. В качестве этих точек принимаются точки пересечения медиан. Процедуры нумерации граней, определения направляющих косинусов их нормалей и определения координат центральных точек весьма упрощается, если точки на поверхности задавать в виде рядов точек с одинаковым числом в каждом ряде.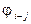 имеет весьма простой вид и его реализация требует относительно небольших затрат компьютерного времени. Допустим, например, что нормаль центральной элементарной площадки
имеет весьма простой вид и его реализация требует относительно небольших затрат компьютерного времени. Допустим, например, что нормаль центральной элементарной площадки  -ой грани имеет направляющие косинусы
-ой грани имеет направляющие косинусы  , а координатами центральной точки этой площадки являются
, а координатами центральной точки этой площадки являются 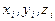 , тогда
, тогда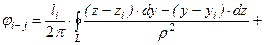
 + +
+ +  (4.1)
(4.1) ,
, - контур
- контур 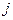 -ой грани - треугольника с известными координатами вершин;
-ой грани - треугольника с известными координатами вершин;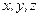 - текущие координаты контура;
- текущие координаты контура; от излучения, исходящего от
от излучения, исходящего от  = 0. Если экранирование отсутствует, то
= 0. Если экранирование отсутствует, то  с плоскостями всех граней, которые могут экранировать излучение, испускаемое
с плоскостями всех граней, которые могут экранировать излучение, испускаемое 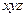 уравнение прямой, проходящей через центральные точки
уравнение прямой, проходящей через центральные точки  и
и  ). Тогда уравнение прямой, проходящей через две заданные точки
). Тогда уравнение прямой, проходящей через две заданные точки 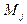 , можно записать в координатной форме:
, можно записать в координатной форме: , (4.2)
, (4.2)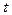 - параметр.
- параметр. ,
, 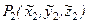 ,
,  . В этом случае уравнение плоскости, проходящей через три заданные точки, можно записать следующим образом:
. В этом случае уравнение плоскости, проходящей через три заданные точки, можно записать следующим образом: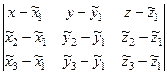 =
= 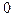 (4.3)
(4.3)
 ,
,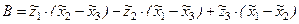 ,
, ,
,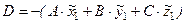 .
. рассматриваемых прямой и плоскости. Значение параметра
рассматриваемых прямой и плоскости. Значение параметра 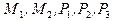 с помощью известного в курсе аналитической геометрии соотношения:
с помощью известного в курсе аналитической геометрии соотношения: ,
,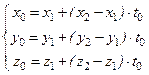
 в пределах отрезка
в пределах отрезка  , сравним сумму расстояний от точки
, сравним сумму расстояний от точки 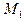 и
и  с расстоянием между точками
с расстоянием между точками  . При этом:
. При этом: ,
, ,
,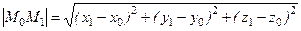 .
. , то это означает, что плоскость грани пересекается с прямой
, то это означает, что плоскость грани пересекается с прямой  . Затенения в этом случае нет. Если
. Затенения в этом случае нет. Если  , пересечение есть, но определенно можно говорить лишь о пересечении отрезка только с плоскостью грани.
, пересечение есть, но определенно можно говорить лишь о пересечении отрезка только с плоскостью грани.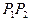 ,
, 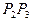 ,
,  , сопоставим площадь треугольника
, сопоставим площадь треугольника 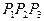
 с суммой площадей треугольников
с суммой площадей треугольников 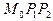 ,
,  ,
,  . В случае равенства отмеченной суммы величине площади треугольника
. В случае равенства отмеченной суммы величине площади треугольника  , можно утверждать, что точка пересечения находится в пределах рассматриваемой грани или на ее границе. Если сумма площадей окажется больше
, можно утверждать, что точка пересечения находится в пределах рассматриваемой грани или на ее границе. Если сумма площадей окажется больше 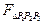 , пересечения с гранью
, пересечения с гранью  и
и 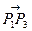 . Векторное произведение этих векторов
. Векторное произведение этих векторов 
 , как известно, можно представить в виде определителя 3-го порядка, 1-ую строку которого образуют орты
, как известно, можно представить в виде определителя 3-го порядка, 1-ую строку которого образуют орты  , а вторую и третью строки - координаты перемножаемых векторов.
, а вторую и третью строки - координаты перемножаемых векторов.


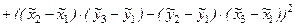

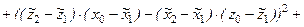
 ,
,

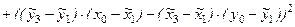 ,
,

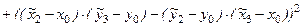 .
. между нормалью элемента
между нормалью элемента 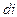
 и вектором
и вектором  превышает
превышает 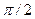 ), то грань не может участвовать в облучении
), то грань не может участвовать в облучении  . Косинус отмеченного угла можно определить разделив скалярное произведение векторов
. Косинус отмеченного угла можно определить разделив скалярное произведение векторов 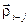 на модуль вектора
на модуль вектора  .
.


