Write(R);3) график заданной функции 4) поэтому нужно проверить значения функции на концах отрезка и выбрать из них наибольшее 5) при t=-10 получаем F(t)=68 6) при t=10 получаем F(t)=148 7) таким образом, ответ: 148. B15 (высокий уровень, время – 10 мин) Тема: Преобразование логических выражений. Что нужно знать: · условные обозначения логических операций A, A Ù B, A Ú B, A → B импликация (следование) A ↔ B, · таблицы истинности логических операций «И», «ИЛИ», «НЕ», «импликация», «эквиваленция» (см. презентацию «Логика») · операцию «импликация» можно выразить через «ИЛИ» и «НЕ»: A → B = A Ú B или в других обозначениях A → B = · операцию «эквиваленция» также можно выразить через «ИЛИ» и «НЕ»: A ↔ B = A Ù B Ú A Ù B или в других обозначениях A ↔ B = · если в выражении нет скобок, сначала выполняются все операции «НЕ», затем – «И», затем – «ИЛИ», потом – «импликация», и самая последняя – «эквиваленция» · логическое произведение A∙B∙C∙… равно 1 (выражение истинно) только тогда, когда все сомножители равны 1 (а в остальных случаях равно 0) · логическая сумма A+B+C+… равна 0 (выражение ложно) только тогда, когда все слагаемые равны 0 (а в остальных случаях равна 1) · правила преобразования логических выражений (законы алгебры логики):
· см. разбор задания А10 (стр.55) Пример задания: Сколько различных решений имеет логическое уравнение (x1 ® x2) Ù (x2 ® x3) Ù (x3 ® x4)= 1 (у1 ® у2) Ù (у2 ® у3) Ù (у3 ® у4) = 1 (Øy1 Ú x1) Ù (Øy2 Ú x2) Ù (Øy3 Ú x3) Ù (Øy4 Ú x4) = 1 где x1, x2, …, x4 и y1, y2, …, y4 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов. Решение: 1) видим, что первые два уравнения независимы друг от друга (в первое входят только x1, x2, …, x4, а во второе – только y1, y2, …, y4) 2) третье уравнение связывает первые два, поэтому можно поступить так: · найти решения первого уравнения · найти решения второго уравнения · найти множество решений первых двух уравнений · из множества решений первых двух уравнений выкинуть те, которые не удовлетворяют последнему уравнению 3) найдем решения первого уравнения; каждая из логических переменных x1, x2, …, x4 может принимать только два значения: «ложь» (0) и «истина» (1), поэтому решение первого уравнения можно записать как битовую цепочку длиной 4 бита: например, 0011 означает, что 4) вспомним, что импликация x1®x2 ложна только для x1 = 1 и x2 = 0, поэтому битовая цепочка, представляющая собой решение первого уравнения, не должна содержать сочетания «10»; это дает такие решения (других нет!): (x1, x2, x3, x4) = 0000 0001 0011 0111 1111 5) видим, что второе уравнение полностью совпадает по форме с первым, поэтому все его решения: (y1, y2, y3, y4) = 0000 0001 0011 0111 1111 6) поскольку первые два уравнения независимы друг от друга, система из первых двух уравнений имеет 5·5=25 решений: каждому решению первого соответствует 5 разных комбинаций переменных y1, y2, …, y4, которые решают второе, и наоборот, каждому решению второго соответствует 5 разных комбинаций переменных x1, x2, …, x4, которые решают первое: (y1, y2, y3, y4) = 0000 0001 0011 0111 1111 (x1, x2, x3, x4) = 0000 0000 0000 0000 0000 0001 0001 0001 0001 0001 0011 0011 0011 0011 0011 0111 0111 0111 0111 0111 1111 1111 1111 1111 1111 7) теперь проверим, какие ограничения накладывает третье уравнение; вспомнив формулу, которая представляет импликацию через операции «НЕ» и «ИЛИ» ( (y1 ® x1) Ù (y2 ® x2) Ù (y3 ® x3) Ù (y4 ® x4) = 1 8) импликация y1®x1 ложна только для y1 = 1 и x1 = 0, следовательно, такая комбинация запрещена, потому что нарушает третье уравнение; таким образом, набору с y1 = 1: (y1, y2, y3, y4) = 1111 соответствует, с учетом третьего уравнения, только одно решение первого, в котором x1 = 1 (y1, y2, y3, y4) = 1111 поэтому множество решений «редеет»: (y1, y2, y3, y4) = 0000 0001 0011 0111 1111 (x1, x2, x3, x4) = 0000 0000 0000 0000 0001 0001 0001 0001 0011 0011 0011 0011 0111 0111 0111 0111 1111 1111 1111 1111 1111 9) аналогично двигаемся дальше по третьему уравнению; второй сомножитель равен 0, если импликация y2®x2 ложна, то есть только для y2 = 1 и x2 = 0, это «прореживает» предпоследний столбец: (y1, y2, y3, y4) = 0000 0001 0011 0111 1111 (x1, x2, x3, x4) = 0000 0000 0000 0001 0001 0001 0011 0011 0011 0111 0111 0111 0111 1111 1111 1111 1111 1111 10) аналогично проверяем еще два ограничения, отбрасывая все решения, для которых y3 = 1 и x3 = 0, а также все решения, для которых y4 = 1 и x4 = 0: (y1, y2, y3, y4) = 0000 0001 0011 0111 1111 (x1, x2, x3, x4) = 0000 0001 0001 0011 0011 0011 0111 0111 0111 0111 1111 1111 1111 1111 1111 11) итак, остается одно решение при (y1, y2, y3, y4)=1111, два решения при (y1, y2, y3, y4)=0111, три решения при (y1, y2, y3, y4)=0011, четыре решения при (y1, y2, y3, y4)=0001 и 5 решений при (y1, y2, y3, y4)=0000 12) всего решений 1+2+3+4+5= 15. Ещё пример задания: Сколько различных решений имеет логическое уравнение X1 → X2 ÚX3 Ù X4 = 1 X3 → X4 ÚX5 Ù X6 = 1 X5 → X6 ÚX1 Ù X2 = 1 где x1, x2, …, x6 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов. Решение: 13) перепишем уравнения в более простом виде, заменим знаки Ú; и Ù; соответственно на (логические) сложение и умножение:
14) вспомним, что сначала выполняется логическое умножение, потом логические сложение и только потом – импликация, поэтому уравнения можно переписать в виде
15) раскрывая импликацию по формуле
16) далее замечаем, что
17) пусть 18) теперь пуст 19) таким образом, система уравнений относительно переменных 20) теперь вернемся обратно к исходным переменным; значению 21) то же самое можно сказать про 22) переменные 23) всего решений 1 + 27 = 28. Ещё пример задания: Сколько различных решений имеет логическое уравнение X1 → X2 → X3 → X4 → X5 → X6 = 1 где x1, x2, …, x6 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов. Решение (вариант 1, табличный метод, динамическое программирование): 24) в левой части заданного уравнения стоят последовательно несколько операций импликации, скобок нет, поэтому порядок выполнения операций определяется приоритетом этих операций; в данном случае все операции имеют одинаковый приоритет 25) операции, имеющие одинаковый приоритет, выполняются слева направо, то есть первой выполняется импликация X1 → X2, а последней – последняя импликация ((((X1 → X2) → X3) → X4) → X5) → X6 26) каждая логическая переменная может принимать значение «истина» (1) или «ложь» (0) 27) для набора из 6 независимых логических переменных существует 26 =64 разных комбинаций значений этих переменных
28) рассмотрим первую импликацию, X1 → X2; она дает в трёх случаях 1, и в одном – 0:
29) посмотрим, как меняется количество решений, если «подключить» следующую переменную; · если X1=0, то X1 → X2 =1 (из · если X1=1, то X1 → X2 =0 при X2 =0 и X1 → X2 =1 при X2 =1 (из 30) исходя из этого, можно составить формулы для вычисления количества нулей
31) для одной переменной имеем 1 ноль и 1 единицу, поэтому начальные условия для расчёта:
32) составим таблицу, которую будем заполнять слева направо, вычисляя число нулей и единиц по приведенным выше формулам; в таблице показано, как строится следующий столбец таблицы для
33) таким образом, ответ: 43 решения. Решение (вариант 2, «с хвоста»): 9) те же рассуждения, что и в п. 1-4 решения по варианту 1 10) если X6 =1, то левая часть уравнения равна 1, то есть равенство выполняется; комбинаций с X6 =1 ровно половина от общего количества, то есть 32 11) теперь проверяем варианты с X6 =0; сразу получаем, что для выполнения заданного уравнения нужно, чтобы (X1 → X2 → X3 → X4 → X5)=0; иначе получим 1 → X6 = 1 →0 = 0 12) проверим отдельно случаи X5=0 и X5=1 13) пусть X6 = 0 и X5 =1; в этом случае никогда не будет выполнено условие 14) пусть X6 = X5 =0; в этом случае условие (X1 → X2 → X3 → X4 → X5)=0 выполняется только при (X1 → X2 → X3 → X4)=1; если X4=1, это условие всегда верно, поэтому получаем еще 8 решений – 8 комбинаций, где X6 = X5 =0 и X4=1 (1/8 всех комбинаций) 15) теперь рассмотрим случаи, когда X6 = X5 = X4=0; рассуждая аналогично, находим, что условие (X1 → X2 → X3 → 0)=1 верно при (X1 → X2 → X3)=0, это сразу дает X3 =0 и 16) при всех известных значениях остальных переменных (X6 = X5 = X4=X3=0) условие 17) таким образом, ответ: 32 + 8 + 3 = 43 решения. Решение (вариант 3, приведение к базису «И-ИЛИ-НЕ», Е.Н. Смирнова): 1) те же рассуждения, что и в п. 1-4 решения по варианту 1 2) заменяем импликацию по формуле
3) далее по той же формуле
инверсию в первом слагаемом раскроем по закону де Моргана (
4) сделав те же операции с оставшейся скобкой, получаем
5) и, применяя ту же формулу еще раз, получим уравнение
6) при 7) при 8) при 9) при 10) таким образом, ответ: 32 + 8 + 3 = 43 решения. Ещё пример задания: Сколько различных решений имеет система уравнений X1 Ú X2 Ù X3 = 1 X2 Ú X3 Ù X4 = 1 ... X8 Ú X9 Ù X10 = 1 где x1, x2, …, x10 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов. Решение (последовательное подключение уравнений): 1) рассмотрим сначала все решения первого уравнения; его левая части истинна, когда X1=1 (при этом X2 и X3 могут быть любыми), а также когда X1=0 и X2=X3 =1:
2) заметим, что первое и второе уравнения связаны через последние две переменных, в данном случае это X2 и X3 3) пусть i – число переменных в уравнениях; введем обозначения: Ki – количество решений, в которых последние две переменные принимают Li – количество решений, в которых последние две переменные принимают Mi – количество решений, в которых последние две переменные принимают Ni – количество решений, в которых последние две переменные принимают 4) из таблицы видим, что K3=1, L3=1, M3=1 и N3=2 5) теперь подключаем второе уравнение; посмотрим, к чему приводят разные комбинации последних двух переменных:
6) находим, что комбинация (1,0) дает два решения, причем (X3,X4)=(0,0) или (0,1) комбинация (1,1) дает два решения, причем (X3,X4)=(1,0) или (1,1) 7) из предыдущего пункта делаем вывод, что Ki+1 = Mi (комбинация (0,0) появилась из (1,0) на предыдущем шаге) Li+1 = Mi (комбинация (0,1) появилась из (1,0) на предыдущем шаге) Mi+1 = Ni (комбинация (1,0) появилась из (1,1) на предыдущем шаге) Ni+1 = Li+Ni (комбинация (1,1) появляется из (0,1) и (1,1))
8) используя эти рекуррентные формулы, заполняем таблицу для i=4,…,10
9) таким образом, ответ: 13 + 13 + 19 + 28 = 73 решения. Ещё пример задания: Сколько различных решений имеет логическое уравнение (X1ÚX2) Ù (X2ÚX3) Ù (X3ÚX4) Ù (X4ÚX5) Ù (X5ÚX6) = 1 где x1, x2, …, x6 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов. Решение: 34) перепишем уравнение, заменив знаки логических операций:
35) учитывая, что
36) решение уравнения можно записать в виде шести двоичных знаков, которые обозначают соответственно, переменные 37) далее вспомним, что импликация дает ложное значение, если её первая часть (посылка) истинна, а вторая (следствие) ложно, поэтому из 38) это значит, что в исходном выражении появится нуль, если в цепочке битов, соответствующей значениям переменных, появится комбинация 10, то есть предыдущее значение истинно, а следующее за ним – ложно 39) поэтому решениями этого уравнения будут все комбинации значений переменных, для которых в соответствующей битовой цепочке нет последовательности 10; 40) таких цепочек всего 7: 000000, 000001, 000011, 000111, 001111, 011111, 111111 41) таким образом, ответ: 7 решений. Ещё пример задания: Сколько различных решений имеет система уравнений X1 Ú X2 = 1 X2 Ú X3 = 1 ... X9 Ú X10 = 1 где x1, x2, …, x10 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов. Решение (табличный метод): 1) рассмотрим все решения первого уравнения
2) строчка, выделенная красным фоном, не удовлетворяет условию, поэтому дальше ее рассматривать не будем 3) теперь подключаем третью переменную и второе уравнение:
4) при каких значениях переменной X3 будет верно условие
5) как видно из таблицы, верхняя строчка предыдущей таблицы (где были все нули) дает два решения при подключении очередного уравнения, а все остальные – по одному 6) понятно, что такая же ситуация будет продолжаться и дальше, то есть, при добавлении каждой новой переменной число решений увеличивается на 1 7) рассуждая таким образом и дальше, получаем, что для 3-х уравнений с 4-мя переменными будет 5 решений, для 4 уравнений – 6 решений, …, а для 9 уравнений – 11 решений 8) обратите внимание на форму таблицы – единицы и нули образуют два треугольника 9) таким образом, ответ: 11 решений.
Еще пример задания: Сколько различных решений имеет система уравнений (X1 º X2) Ú (X3 º X4) = 1 (X3 º X4) Ú (X5 º X6) = 1 (X5 º X6) Ú (X7 º X8) = 1 (X7 º X8) Ú (X9 º X10) = 1 где x1, x2, …, x10 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов. Решение: 1) количество комбинаций 10 логических переменных равно 210 = 1024, поэтому вариант с построением полной таблицы истинности отпадает сразу 2) заметим, что при обозначениях Y1 Ú Y2 = 1 Y2 Ú Y3 = 1 Y3 Ú Y4 = 1 Y4 Ú Y5 = 1 3) как следует из разбора предыдущей задачи, такая система имеет 5+1 = 6 решений для переменных Y1 … Y5 4) теперь нужно получить количество решений в исходных переменных, X1 … X10; для этого заметим, что переменные Y1 … Y5 независимы; 5) предположим, что значение Y1 известно (0 или 1); поскольку 6) у нас есть 5 переменных Y1 … Y5, каждая их комбинация дает 2 пары (X1;X2), 2 пары (X3;X4), 2 пары (X5;X6), 2 пары (X7;X8) и 2 пары (X9;X10), то есть всего 25 = 32 комбинации исходных переменных 7) таким образом, общее количество решений равно 6 ·32 = 192 8) ответ: 192 решения Еще пример задания: Сколько различных решений имеет система уравнений (X1ÙX2) Ú (X1ÙX2) Ú (X3ÙX4) Ú (X3ÙX4) = 1 (X3ÙX4) Ú (X3ÙX4) Ú (X5ÙX6) Ú (X5ÙX6) = 1 (X5ÙX6) Ú (X5ÙX6) Ú (X7ÙX8) Ú (X7ÙX8) = 1 (X7ÙX8) Ú (X7ÙX8) Ú (X9ÙX10) Ú (X9ÙX10) = 1 где x1, x2, …, x10 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов. Решение: 1) количество комбинаций 10 логических переменных равно 210 = 1024, поэтому вариант с построением полной таблицы истинности отпадает сразу 2) решать такую систему «в лоб» достаточно сложно, нужно попробовать ее упростить 3) заметим, что (X1ÙX2) Ú (X1ÙX2) = (X1 º X2), где символ º; означает операцию «эквивалентность» (значения равны); 4) кроме того, (X3ÙX4) Ú (X3ÙX4) = (X3 Å X4) = (X3 º X4), где символ Å; означает операцию «исключающее ИЛИ» (значения НЕ равны); это операция, обратная эквивалентности 5) используем замену переменных, выделив члены, объединяющие пары исходных переменных (X1 и X2, X3 и X4, X5 и X6, X7 и X8, X9 и X10) Y1 = (X1 º X2) Y2 = (X3 º X4) Y3 = (X5 º X6) Y4 = (X7 º X8) Y5 = (X9 º X10) 6) при этих обозначения система уравнений преобразуется к виду Y1 Ú Y2 = 1 Y2 Ú Y3 = 1 Y3 Ú Y4 = 1 Y4 Ú Y5 = 1 9) как показано выше (при разборе пред-предыдущей задачи), такая система имеет 5+1 = 6 решений для независимых переменных Y1 … Y5 10) предположим, что значение Y1 известно (0 или 1); поскольку 11) у нас есть 5 переменных Y1 … Y5, каждая их комбинация дает 2 пары (X1;X2), 2 пары (X3;X4), 2 пары (X5;X6), 2 пары (X7;X8) и 2 пары (X9;X10), то есть всего 25 = 32 комбинации исходных переменных 12) таким образом, общее количество решений равно 6 ·32 = 192 7) ответ: 192 решения Ещё пример задания: Каково наибольшее целое число X, при котором истинно высказывание (50 < X·X) → (50 > (X+1)·(X+1)) Решение (вариант 1): 39) это операция импликации между двумя отношениями 40) попробуем сначала решить неравенства
41)
обозначим эти области на оси X: на рисунке фиолетовые зоны обозначают область, где истинно выражение 42) вспомним таблицу истинности операции «импликация»:
43) согласно таблице, заданное выражение истинно везде, кроме областей, где 44) поэтому наибольшее целое число, удовлетворяющее условию – это первое целое число, меньшее 45) таким образом, верный ответ – 7.
Решение (вариант 2, преобразование выражения): 1) сначала можно преобразовать импликацию, выразив ее через «ИЛИ» и «НЕ»:
2) это значит, что выражение истинно там, где 3) дальнейшие действия точно такие же, как и в варианте 1.
Еще пример задания: Каково наибольшее целое число X, при котором истинно высказывание (10 < X·(X+1)) → (10 > (X+1)·(X+2)) Решение (в целых числах): 1) это операция импликации между двумя отношениями:
2) конечно, здесь можно применить тот же способ, что и в предыдущем примере, однако при этом понадобится решать квадратные уравнения (не хочется…) 3) заметим, что по условию нас интересуют только целые числа, поэтому можно попытаться как-то преобразовать исходное выражение, получив равносильное высказывание (как понятно из предыдущего примера, точные значения корней нас совершенно не интересуют!) 4) рассмотрим неравенство 5) легко проверить, что в области
|

 – это парабола, ветви которой направлены вверх, то есть она имеет точку минимума, но не точку максимума
– это парабола, ветви которой направлены вверх, то есть она имеет точку минимума, но не точку максимума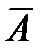 не A (отрицание, инверсия)
не A (отрицание, инверсия) A и B (логическое умножение, конъюнкция)
A и B (логическое умножение, конъюнкция) A или B (логическое сложение, дизъюнкция)
A или B (логическое сложение, дизъюнкция) эквиваленция (эквивалентность, равносильность)
эквиваленция (эквивалентность, равносильность)






 ), можно переписать третье уравнение в виде
), можно переписать третье уравнение в виде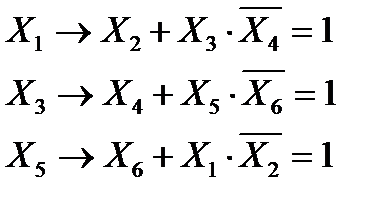
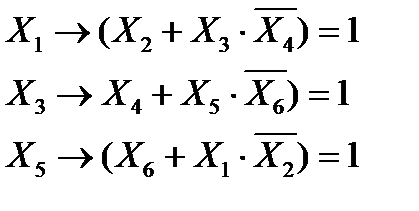
 , получаем
, получаем
 ,
,  и
и  , поэтому можно ввести новые переменные
, поэтому можно ввести новые переменные  ,
,  и
и 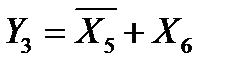 , и переписать уравнения в виде
, и переписать уравнения в виде
 , тогда из первого уравнения сразу имеем
, тогда из первого уравнения сразу имеем 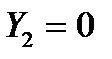 и далее из второго
и далее из второго  ; при этом третье автоматически выполняется; получили одно решение
; при этом третье автоматически выполняется; получили одно решение , тогда из последнего уравнения имеем
, тогда из последнего уравнения имеем  , а из второго –
, а из второго –  , при этом первое уравнение справедливо
, при этом первое уравнение справедливо имеет два решения: (0,0,0) и (1,1,1)
имеет два решения: (0,0,0) и (1,1,1)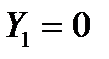 соответствует единственный вариант
соответствует единственный вариант  ; значению
; значению  соответствуют остальные 3 пары возможных значений
соответствуют остальные 3 пары возможных значений 
 и
и  : нулевое значение дает один набор соответствующих исходных переменных, а единичное – три
: нулевое значение дает один набор соответствующих исходных переменных, а единичное – три ,
,  нулей получаются
нулей получаются  единиц)
единиц)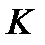 единиц получаются
единиц получаются  и количества единиц
и количества единиц  для уравнения с
для уравнения с  переменными:
переменными: ,
, 

 :
: ; на первом шаге получаем
; на первом шаге получаем

 ):
):


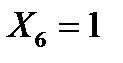 остальные 5 переменных можно выбирать любым способом, это дает 25 = 32 решения4444444
остальные 5 переменных можно выбирать любым способом, это дает 25 = 32 решения4444444 и
и  решений нет
решений нет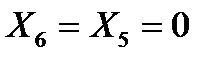 получаем 23 = 8 решений при
получаем 23 = 8 решений при  (можно выбирать
(можно выбирать 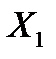 ,
,  и
и  произвольно)
произвольно) сразу находим, что
сразу находим, что  , это дает еще 3 решения, при которых истинно выражение
, это дает еще 3 решения, при которых истинно выражение 

 , заменяем все выражения в скобках на импликацию:
, заменяем все выражения в скобках на импликацию:

 сразу следует, что
сразу следует, что 
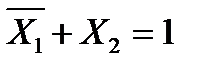 по таблице истинности:
по таблице истинности: ? Очевидно, что на это уже не влияет X1 (этот столбец выделен зеленым цветом). Если X2 = 1, то сразу получаем, что X3 = 1 (иначе
? Очевидно, что на это уже не влияет X1 (этот столбец выделен зеленым цветом). Если X2 = 1, то сразу получаем, что X3 = 1 (иначе 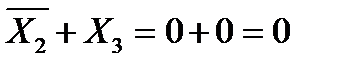 ):
): ,
,  ,
,  ,
,  и
и  мы получаем систему из 4 уравнений и 5 независимыми переменными; эта система уравнений относится к типу, который рассмотрен в предыдущей разобранной задаче:
мы получаем систему из 4 уравнений и 5 независимыми переменными; эта система уравнений относится к типу, который рассмотрен в предыдущей разобранной задаче: , по таблице истинности операции «эквивалентность» есть две соответствующих пары (X1;X2) (как для случая Y1 = 0, так и для случая Y1 = 1)
, по таблице истинности операции «эквивалентность» есть две соответствующих пары (X1;X2) (как для случая Y1 = 0, так и для случая Y1 = 1)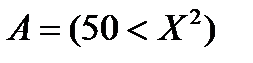 и
и 
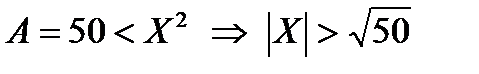 ,
, 







 , голубая зона – это область, где истинно
, голубая зона – это область, где истинно 
 и
и  ; область истинности выделена зеленым цветом
; область истинности выделена зеленым цветом , то есть, 7
, то есть, 7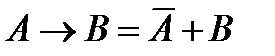
 или
или 
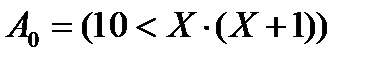 и
и 
 : очевидно, что
: очевидно, что  может быть как положительным, так и отрицательным числом;
может быть как положительным, так и отрицательным числом; высказывание
высказывание  истинно при всех целых
истинно при всех целых 


