Определение 4. Множество  называется всюду плотным в множестве
называется всюду плотным в множестве  , если
, если  , т.е. замыкание множества
, т.е. замыкание множества  содержит
содержит  .
.
Определение 5. Множество  называется всюду плотным в метрическом пространстве
называется всюду плотным в метрическом пространстве  , если
, если  , т.е. замыкание
, т.е. замыкание  совпадает со всем пространством
совпадает со всем пространством  .
.
Теорема 1. Всякое метрическое пространство  имеет пополнение
имеет пополнение  .
.
Доказательство. Назовем две фундаментальные последовательности  и
и  эквивалентными, если
эквивалентными, если  . Если
. Если 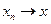 , то
, то
 ,
,
и потому  . Таким образом, если одна из эквивалентных последовательностей сходится, то и другая сходится к той же точке.
. Таким образом, если одна из эквивалентных последовательностей сходится, то и другая сходится к той же точке.
А теперь разобьем множество всех фундаментальных последовательностей на классы, отнеся в один класс все эквивалентные между собой последовательности. Обозначим через  множество таких классов. Как следует из аксиомы треугольника две последовательности, эквивалентные третьей, эквивалентны между собой. Одна и та же последовательность не может принадлежать разным классам.
множество таких классов. Как следует из аксиомы треугольника две последовательности, эквивалентные третьей, эквивалентны между собой. Одна и та же последовательность не может принадлежать разным классам.
Пусть 
 и
и  два класса из множества
два класса из множества  . Выберем в классе
. Выберем в классе  фундаментальную последовательность
фундаментальную последовательность  , а в классе
, а в классе  -
-  . Из неравенства (1.1) получаем
. Из неравенства (1.1) получаем
 .
.
Это означает, что числовая последовательность  сходится. Полагая
сходится. Полагая
 , (2.1)
, (2.1)
мы определим расстояние во множестве  . Покажем, что это расстояние не зависит от выбора представителей классов. Если последовательность
. Покажем, что это расстояние не зависит от выбора представителей классов. Если последовательность  эквивалентна
эквивалентна  , а
, а  эквивалентна
эквивалентна  , то переходя к пределу в неравенстве
, то переходя к пределу в неравенстве
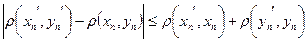
получим
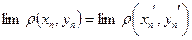 . (2.2)
. (2.2)
Теперь нужно проверить, что расстояние, определенное формулой (2.1) удовлетворяет аксиомам метрического пространства. Первые две аксиомы проверяются без труда. Остановимся на аксиоме треугольника. Пусть  ,
,  и
и  - последовательности, принадлежащие соответственно классам
- последовательности, принадлежащие соответственно классам  ,
,  и
и  . Имеем
. Имеем
 .
.
Переходя в этом неравенстве к пределу, получим аксиому треугольника. Следовательно, построено некоторое метрическое пространство  .
.
Теперь построим изометрию метрического пространства  на подмножество
на подмножество  метрического пространства
метрического пространства  :
:  .
.
Каждому элементу  поставим в соответствие класс
поставим в соответствие класс  последовательностей, сходящихся к элементу
последовательностей, сходящихся к элементу  . Этот класс не пуст, поскольку содержит стационарную последовательность
. Этот класс не пуст, поскольку содержит стационарную последовательность 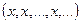 . Очевидно,
. Очевидно,
 ,
,
поскольку в качестве определяющих классы  и
и  можно взять последовательности
можно взять последовательности 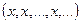 и
и  . Итак пространство
. Итак пространство  изометрично
изометрично  .
.
Далее покажем, что  всюду плотно в метрическом пространстве
всюду плотно в метрическом пространстве  , т.е. замыкание
, т.е. замыкание  совпадает со всем пространством
совпадает со всем пространством  .
.
Пусть  - произвольный элемент из
- произвольный элемент из  и
и  - определяющая для этого класса фундаментальная последовательность. Обозначим через
- определяющая для этого класса фундаментальная последовательность. Обозначим через  стационарную последовательность, т.е.
стационарную последовательность, т.е. 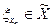 . Докажем, что
. Докажем, что  в пространстве
в пространстве  . Так как последовательность
. Так как последовательность  фундаментальна, то для любого
фундаментальна, то для любого  существует число
существует число  такое, что
такое, что
 ,
,  .
.
Отсюда и из определения расстояния в пространстве  получаем
получаем
 ,
,  .
.
А это и означает, что  в пространстве
в пространстве  . И по предложению 9 множество
. И по предложению 9 множество  плотно в пространстве
плотно в пространстве  .
.
Наконец, в заключении, докажем полноту пространства  . Возьмем фундаментальную в
. Возьмем фундаментальную в  последовательность точек
последовательность точек  .Так как
.Так как  плотно в пространстве
плотно в пространстве  , то для
, то для  найдется элемент
найдется элемент  такой, что
такой, что  . С учетом неравенства треугольника имеем
. С учетом неравенства треугольника имеем
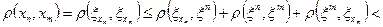
 .
.
Из этого неравенства, учитывая фундаментальность последовательности  , получим, что последовательность
, получим, что последовательность  также является фундаментальной и поэтому представляет некоторый класс
также является фундаментальной и поэтому представляет некоторый класс  . Снова из неравенства треугольника имеем
. Снова из неравенства треугольника имеем
 .
.
Отсюда окончательно получаем, что  . Теорема полностью доказана.
. Теорема полностью доказана.
Замечание. В виду того, что пространство  изометрично множеству
изометрично множеству  , то мы можем отождествлять их элементы. Это учтем в следующей теореме.
, то мы можем отождествлять их элементы. Это учтем в следующей теореме.
Теорема 2. Пополнение метрического пространства  единственно с точностью до изометрии, оставляющей неподвижными точки из
единственно с точностью до изометрии, оставляющей неподвижными точки из  .
.
Доказательство. Пусть  и
и  два пополнения пространства
два пополнения пространства  . Нужно доказать существование такого взаимно однозначного отображения
. Нужно доказать существование такого взаимно однозначного отображения  пространства
пространства  на
на  , что
, что
1)  ;
;
2) если 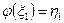 и
и  , то
, то  , где
, где  - расстояние в
- расстояние в  , а
, а  - расстояние в
- расстояние в  .
.
Возьмем произвольный элемент  . По определению пополнения существует последовательность
. По определению пополнения существует последовательность  точек из
точек из  , сходящаяся к
, сходящаяся к  . Так как пространство
. Так как пространство  - полно, а последовательность
- полно, а последовательность  - фундаментальна, то она сходится и в пространстве
- фундаментальна, то она сходится и в пространстве  к некоторой точке
к некоторой точке  . Положим
. Положим 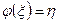 . Отображение
. Отображение  и есть искомая изометрия.
и есть искомая изометрия.
В самом деле, по построению,  для всех
для всех  . Далее, пусть
. Далее, пусть
 в
в  и
и  в
в  ,
,
 в
в  и
и  в
в  ,
,
тогда в силу непрерывности расстояния,
 ,
,
 .
.
Отсюда следует, что
 .
.
И теорема доказана.

 называется всюду плотным в множестве
называется всюду плотным в множестве  , если
, если  , т.е. замыкание множества
, т.е. замыкание множества  , если
, если  , т.е. замыкание
, т.е. замыкание  .
. и
и  эквивалентными, если
эквивалентными, если  . Если
. Если 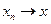 , то
, то ,
, . Таким образом, если одна из эквивалентных последовательностей сходится, то и другая сходится к той же точке.
. Таким образом, если одна из эквивалентных последовательностей сходится, то и другая сходится к той же точке.
 и
и  два класса из множества
два класса из множества  . Из неравенства (1.1) получаем
. Из неравенства (1.1) получаем .
. сходится. Полагая
сходится. Полагая , (2.1)
, (2.1) эквивалентна
эквивалентна 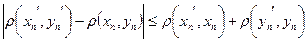
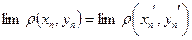 . (2.2)
. (2.2) - последовательности, принадлежащие соответственно классам
- последовательности, принадлежащие соответственно классам  . Имеем
. Имеем .
. метрического пространства
метрического пространства  .
. поставим в соответствие класс
поставим в соответствие класс  последовательностей, сходящихся к элементу
последовательностей, сходящихся к элементу  . Этот класс не пуст, поскольку содержит стационарную последовательность
. Этот класс не пуст, поскольку содержит стационарную последовательность 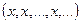 . Очевидно,
. Очевидно, ,
, можно взять последовательности
можно взять последовательности  . Итак пространство
. Итак пространство  стационарную последовательность, т.е.
стационарную последовательность, т.е. 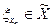 . Докажем, что
. Докажем, что  в пространстве
в пространстве  существует число
существует число  ,
,  .
. ,
,  .
. .Так как
.Так как  найдется элемент
найдется элемент  такой, что
такой, что  . С учетом неравенства треугольника имеем
. С учетом неравенства треугольника имеем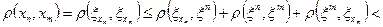
 .
. , получим, что последовательность
, получим, что последовательность  .
. . Теорема полностью доказана.
. Теорема полностью доказана. изометрично множеству
изометрично множеству  , то мы можем отождествлять их элементы. Это учтем в следующей теореме.
, то мы можем отождествлять их элементы. Это учтем в следующей теореме. и
и  два пополнения пространства
два пополнения пространства  пространства
пространства  ;
;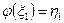 и
и  , то
, то  , где
, где  - расстояние в
- расстояние в  - расстояние в
- расстояние в  . По определению пополнения существует последовательность
. По определению пополнения существует последовательность  точек из
точек из  . Так как пространство
. Так как пространство  . Положим
. Положим 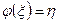 . Отображение
. Отображение  для всех
для всех  в
в  в
в  в
в  в
в  ,
, .
.


