Определение 8. Если каждому элементу  некоторого непустого множества
некоторого непустого множества  поставлено в соответствие некоторое множество, то говорят, что задано семейство
поставлено в соответствие некоторое множество, то говорят, что задано семейство  или лаконично -
или лаконично -  .
.
Определение 9. Семейство  открытых подмножеств метрического пространства
открытых подмножеств метрического пространства  называется открытым покрытием
называется открытым покрытием  , если
, если  .
.
Определение 10. Часть семейства  , которая сама является покрытием
, которая сама является покрытием  называется подпокрытием.
называется подпокрытием.
Теорема 2. Для метрического пространства следующие свойства эквивалентны:
1) метрическое пространство компактно;
2) у любого открытого покрытия пространства существует конечное подпокрытие.
Докажем вначале, что из 2) следует 1). Согласно предложения 1, пространство компактно тогда и только тогда, когда каждое бесконечное подмножество имеет предельную точку.
Предположим, что бесконечное подмножество  не имеет предельных точек. Отсюда следует, в частности, что подмножество
не имеет предельных точек. Отсюда следует, в частности, что подмножество  замкнуто. Далее, у каждой точки
замкнуто. Далее, у каждой точки 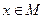 есть окрестность
есть окрестность  , не содержащая других точек из
, не содержащая других точек из  . Семейство, состоящее из
. Семейство, состоящее из  и всех множеств
и всех множеств  ,
, 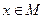 , образует открытое покрытие пространства
, образует открытое покрытие пространства  , не обладающее конечным подпокрытием. Полученное противоречие доказывает часть теоремы.
, не обладающее конечным подпокрытием. Полученное противоречие доказывает часть теоремы.
Докажем теперь, что из 1) следует 2). Мы предполагаем, что пространство  компактно и поэтому вполне ограничено и полно. Предположим, что существует открытое покрытие
компактно и поэтому вполне ограничено и полно. Предположим, что существует открытое покрытие  пространства
пространства  , никакое конечное подсемейство которого не покрывает
, никакое конечное подсемейство которого не покрывает  .
.
Используя то, что  вполне ограничено, построим его покрытие конечным числом шаров радиуса
вполне ограничено, построим его покрытие конечным числом шаров радиуса 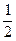 . Найдется шар
. Найдется шар 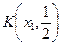 , который не может быть покрыт конечным подсемейством из
, который не может быть покрыт конечным подсемейством из  . Шар
. Шар 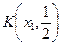 также является вполне ограниченным. Покрывая его конечным числом шаров радиуса
также является вполне ограниченным. Покрывая его конечным числом шаров радиуса  , найдем шар
, найдем шар  , пересекающийся с
, пересекающийся с 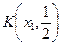 и который не может быть покрыт конечным подсемейством из
и который не может быть покрыт конечным подсемейством из  .
.
Продолжая рассуждения, построим последовательность шаров  , ни один из которых не может быть покрыт конечным подсемейством из
, ни один из которых не может быть покрыт конечным подсемейством из  и таких,что пересечения
и таких,что пересечения  непусты. Отсюда, применяя неравенство треугольника, найдем
непусты. Отсюда, применяя неравенство треугольника, найдем
 .
.
Из этого неравенства вытекает, что центры шаров образуют фундаментальную последовательность  . И поскольку пространство
. И поскольку пространство  полно, то последовательность
полно, то последовательность  сходится к некоторой точке
сходится к некоторой точке 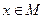 . Эта точка
. Эта точка  должна принадлежать хотя бы одному множеству семейства
должна принадлежать хотя бы одному множеству семейства  , например, множеству
, например, множеству  . Так как множество
. Так как множество  открыто, то вместе с точкой
открыто, то вместе с точкой  оно содержит открытый шар: существует такое число
оно содержит открытый шар: существует такое число  , что
, что  .
.
Теперь выберем 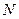 так, чтобы одновременно выполнялись два неравенства
так, чтобы одновременно выполнялись два неравенства  и
и  . Тогда верно включение
. Тогда верно включение  . В самом деле, если
. В самом деле, если  , то по неравенству треугольника имеем
, то по неравенству треугольника имеем  .
.
Следовательно, шар  содержится в одном открытом множестве семейства. Получили противоречие с тем, что шар
содержится в одном открытом множестве семейства. Получили противоречие с тем, что шар  не может быть покрыт конечным подсемейством из
не может быть покрыт конечным подсемейством из  . Теорема полностью доказана.
. Теорема полностью доказана.
Приведем лемму, которая характеризует компактные пространства.
Лемма. Пусть  - открытое покрытие компактного пространства
- открытое покрытие компактного пространства  . Тогда существует такое число
. Тогда существует такое число  , что любой шар с произвольным центром радиуса
, что любой шар с произвольным центром радиуса 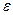 будет полностью содержаться хотя бы в одном из открытых множеств покрытия.
будет полностью содержаться хотя бы в одном из открытых множеств покрытия.
Доказательство. Предположим противное. Тогда для любого 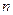 можно найти такую точку
можно найти такую точку 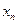 , что шар
, что шар  не лежит целиком ни в одном из открытых множеств покрытия
не лежит целиком ни в одном из открытых множеств покрытия  . Последовательность
. Последовательность  имеет подпоследовательность, сходящуюся к некоторой точке
имеет подпоследовательность, сходящуюся к некоторой точке  , так как пространство
, так как пространство  компактно. Эта точка
компактно. Эта точка  должна принадлежать хотя бы одному множеству семейства, например, множеству
должна принадлежать хотя бы одному множеству семейства, например, множеству  . И поскольку множество
. И поскольку множество  открыто, то вместе с точкой
открыто, то вместе с точкой  оно содержит открытый шар: существует такое число
оно содержит открытый шар: существует такое число  , что
, что  .
.
Как и в теореме 2, можем найти такое число 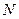 , чтобы
, чтобы  . А это противоречит тому, что шар
. А это противоречит тому, что шар  не содержится целиком ни в одном из открытых множеств покрытия. Лемма доказана.
не содержится целиком ни в одном из открытых множеств покрытия. Лемма доказана.
С помощью леммы приведем еще одно доказательство теоремы 2.
Второй способ доказательства теоремы 2. Нужно доказать, что из любого покрытия  компактного пространства можно выделить конечное подпокрытие. Согласно лемме, существует такое число
компактного пространства можно выделить конечное подпокрытие. Согласно лемме, существует такое число  , что каждый шар радиуса
, что каждый шар радиуса 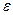 полностью лежит хотя бы в одном из открытых множеств покрытия
полностью лежит хотя бы в одном из открытых множеств покрытия  . Используя вполне ограниченность пространства
. Используя вполне ограниченность пространства  , построим его покрытие конечным числом шаров радиуса
, построим его покрытие конечным числом шаров радиуса 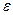 . Обозначим эти шары лаконично через
. Обозначим эти шары лаконично через 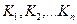 . Каждый шар
. Каждый шар 
 , по лемме, целиком содержится в некотором открытом множестве
, по лемме, целиком содержится в некотором открытом множестве  .
.
И мы построили конечное число открытых множеств  , которые покрывают пространство
, которые покрывают пространство  . Доказательство завершено.
. Доказательство завершено.
В теории метрических и особенно топологических пространств используется другое определение компактного пространства.
Определение 11. Метрическое пространство  называется компактным, если у
называется компактным, если у
любого открытого покрытия пространства  существует конечное подпокрытие.
существует конечное подпокрытие.
Согласно теореме 2, определения 1 и 11 эквивалентны.

 некоторого непустого множества
некоторого непустого множества  поставлено в соответствие некоторое множество, то говорят, что задано семейство
поставлено в соответствие некоторое множество, то говорят, что задано семейство  или лаконично -
или лаконично -  .
. называется открытым покрытием
называется открытым покрытием  .
. не имеет предельных точек. Отсюда следует, в частности, что подмножество
не имеет предельных точек. Отсюда следует, в частности, что подмножество  замкнуто. Далее, у каждой точки
замкнуто. Далее, у каждой точки 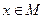 есть окрестность
есть окрестность  , не содержащая других точек из
, не содержащая других точек из  и всех множеств
и всех множеств 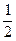 . Найдется шар
. Найдется шар 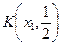 , который не может быть покрыт конечным подсемейством из
, который не может быть покрыт конечным подсемейством из  , найдем шар
, найдем шар  , пересекающийся с
, пересекающийся с  , ни один из которых не может быть покрыт конечным подсемейством из
, ни один из которых не может быть покрыт конечным подсемейством из  непусты. Отсюда, применяя неравенство треугольника, найдем
непусты. Отсюда, применяя неравенство треугольника, найдем .
. . И поскольку пространство
. И поскольку пространство  должна принадлежать хотя бы одному множеству семейства
должна принадлежать хотя бы одному множеству семейства  . Так как множество
. Так как множество  , что
, что  .
.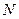 так, чтобы одновременно выполнялись два неравенства
так, чтобы одновременно выполнялись два неравенства  и
и  . Тогда верно включение
. Тогда верно включение  . В самом деле, если
. В самом деле, если  , то по неравенству треугольника имеем
, то по неравенству треугольника имеем  .
. содержится в одном открытом множестве семейства. Получили противоречие с тем, что шар
содержится в одном открытом множестве семейства. Получили противоречие с тем, что шар  , что любой шар с произвольным центром радиуса
, что любой шар с произвольным центром радиуса 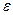 будет полностью содержаться хотя бы в одном из открытых множеств покрытия.
будет полностью содержаться хотя бы в одном из открытых множеств покрытия.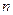 можно найти такую точку
можно найти такую точку 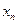 , что шар
, что шар  не лежит целиком ни в одном из открытых множеств покрытия
не лежит целиком ни в одном из открытых множеств покрытия 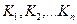 . Каждый шар
. Каждый шар 
 , по лемме, целиком содержится в некотором открытом множестве
, по лемме, целиком содержится в некотором открытом множестве  .
. , которые покрывают пространство
, которые покрывают пространство 


