Точное и среднее значение физической величиныНаша марксистско-ленинская философия (а другой, собственно, у нас как не было, так и нет) всегда утверждала, что только практика является верховным судьей истинности теории. В пику практикам, позволю себе одну старую байку про экспериментаторов, которые изучали воздействие магнитного поля на мозг. В квантовой механике Эйнштейновское «только теория решает, что на самом деле мы ухитряемся наблюдать» особенно актуально. В соответствии с третьим постулатом, если состояние нашей частицы описывается волновой функцией y, являющейся собственной функцией оператора некоторой физической величины
А вот что будет, если функция y, описывающая состояние нашей системы, не является собственной функцией оператора измеряемой физической величины A? В соответствии с третьим постулатом, при измерении мы каждый раз будем получать какое-то из собственных значений ak этого оператора. Результат каждого конкретного измерения при этом предсказать нельзя. Пусть оператору
определяет среднее значение или математическое ожидание измеряемой величины А. При этом
не может быть выведено из предыдущих постулатов, и должно рассматриваться как дополнительный, четвертый постулат. Еще раз подчеркнем: в квантовой механике физическая величина имеет определенное значение в данном состоянии y только в том случае, когда волновая функция, описывающая состояние системы, является собственной функцией оператора, соответствующего данной физической величине. Во всех остальных случаях речь может идти лишь о среднем значении. Это утверждение имеет неожиданное и эффектное продолжение. Рассмотрим две физические величины А и В. Допустим, что наша система находится в состоянии y, описываемой собственной функцией оператора А если операторы не коммутируют, а y – собственная функция Наконец, если функция, описывающая состояние нашей системы, не является собственной ни для Еще раз: если два оператора имеют одинаковую систему собственных функций, то они могут одновременно иметь определенные значения, т.е. быть одновременно измеримыми с любой заданной точностью. В противном случае возникает разброс значений. Насколько велик этот разброс? Мерой разброса значений физической величины Х может служить величина дисперсии – квадрата отклонения от среднего
Нас будет интересовать ожидаемое значение дисперсии В общем случае можно записать, что если
Это выражение суть общая формулировка соотношения неопределенностей Гейзенберга. Применим это выражение к операторам компоненты импульса рх и координаты х. Мы уже знаем, что [ px,x ] = – iħ, т.е.
Вам, наверное, уже случалось видеть его в другом виде, однако тут уже вопрос выбора того, что такое Δ Х. Для нас очень важен качественный результат: координата и импульс микрообъекта не могут быть одновременно измерены точно. В этой формулировке нет лишних слов. Студент часто выдает что-нибудь вроде: «Нельзя измерить координату и импульс электрона» «Координату и импульс электрона нельзя измерить точно» «Нельзя одновременно измерить координату и импульс электрона»
Классическая механика считает, что координату и импульс (или, что то же самое, скорость) любого объекта можно измерить с произвольной точностью. Действительно, возьмем очень маленький шарик массы m = 1 мг. Определим с помощью микроскопа его положение с погрешностью Δ x ≈ 10–5 см. (на самом деле для этого понадобится очень-очень хороший оптический микроскоп). Тогда неопределенность скорости Δ υx = Δ рx/m ≈ ħ /(Δ x m) ~ 10–19 см/с. Такая величина недоступна никакому измерению, а потому и отступление от классического описания совершенно несущественно. И даже для частицы массой 1 мкг величина ħ остается слишком малой.
Другое дело, когда мы имеем дело с микрообъектом с массой покоя 10–27 г, положение которого хочется определить с точностью в тысячу раз большей. Тут уже постоянная Планка 10–34 Дж×с сравнима с измеряемыми величинами. Для иллюстрации принципа неопределенности часто приводят разнообразные мысленные эксперименты. Отметим, что мы уже обращали внимание на проблемы определением положения и длины волны волны-частицы. Самым распространенным из них является мысленное разглядывание движущегося по некоторой траектории электрона в микроскоп. Если длина волны будет сравнительно большой, мы не увидим четкой картинки. Все, что можно сказать: частица должна быть где-то в этом коридоре. Попробуем взять свет с меньшей длиной волны. Теперь картинка будет более четкой, но излучение будет сбивать частицу с ее траектории. Она опять «где-то здесь», но точно сказать, как она повела бы себя в отсутствие прибора, мы не можем. Этот результат дает основу для очень важной интерпретации: если в макромире мы можем считать воздействие прибора на изучаемый объект сколь угодно малым, то при изучении микрообъектов пренебречь влиянием прибора уже нельзя: измерение необходимо вносит изменения в состояние нашего объекта.
Мне, однако, не очень нравится такая интерпретация: она оставляет надежду подобрать подходящие условия, позволяющие получить требуемые значения. Это как с вечным двигателем. Ошибка в каждом конкретном случае все равно находится, но попытки не прекращаются. М.Г. Веселов: Оставаясь на почве классических представлений, мы должны были бы заключить о принципиальной невозможности одновременного сколь угодно точного измерения координат и скорости. В действительности этот результат свидетельствует о неправомочности постановки задачи. Вопрос о том, «можно ли одновременно измерить точно координаты и скорость частицы», предполагающий априорное существование этих свойств, должен быть заменен вопросом: «может ли частица обладать одновременно определенными координатами и скоростью» – и на этот вопрос природа дает отрицательный ответ. Тем самым мы должны прийти к выводу: для описания поведения частицы неприменимо классическое понятие траектории. Приняв это утверждение, мы отчасти отвечаем и критикам постулатов Бора. Вы помните, что основой такой критики был вопрос: каким образом электрон в атоме движется по криволинейной траектории, не излучая? У нас есть, по крайней мере, встречный вопрос: а кто сказал, что электрон в атоме движется по криволинейной траектории? Кстати, принцип неопределенности позволяет рассмотреть проблему устойчивости атома и более подробно. Пусть электрон где-то в атоме, поэтому неопределенность в его положении равна размеру этого атома: D х» 10–8 см. Примем, что величина импульса не превосходит погрешности его определения:
Кинетическая энергия этого электрона А теперь предположим, что электрон упал-таки на ядро, размер которого всего D х» 10–13 см. Заметим, что теперь он притягивается к ядру в 105 раз сильнее! Но справа-то у нас константа, поэтому D р должна вырасти по крайней мере в те же 105 раз. Что произойдет с кинетической энергией?
Другое соотношение неопределенностей связывает энергию и время:
Здесь, однако, следует сделать оговорку: на самом деле время в квантовой механике играет роль параметра, определяемого часами, находящимися вне квантовой системы. Иными словами, у нас нет оператора времени. Поэтому под неопределенностью во времени понимают то обстоятельство, что измерение свойства или воздействие на квантовую систему происходит не мгновенно, а в течение промежутка времени Dt. Можно связать точность изменения энергии спектрального уровня со временем жизни возбужденного состояния. Такой эффект, действительно, существует и проявляется в том, что спектральные линии не являются бесконечно узкими, а имеют т.н. естественную ширину – тем большую, чем меньше время жизни соответствующего возбужденного состояния.
Завершая разговор об измерениях, коммутаторах и прочем упомянем еще об одном коммутационном соотношении. Оно нам почти не понадобится, но все-таки… Гейзенберг строил свою матричную механику, принимая в качестве одного из основных постулатов утверждение, что
– т.е. коммутатор между матрицей, задающей некоторое свойство, и матрицей оператора Гамильтона связан с производной данной величины по времени. Если А коммутирует с Н, то эта величина не изменяется во времени и является постоянной движения. Заметим, что мы с самого начала рассматривали не зависящее от времени уравнение Шредингера. Когда мы его набрасывали из уравнения распространения волны, мы сразу избавились от временной зависимости, а строя уравнение на основе постулатов вообще сразу приняли за основу Гамильтонову функцию, в которой полная энергия сохраняется. В общем случае уравнение Шредингера записывается в виде:
или
и это уравнение тоже входит в набор постулатов квантовой механики.
Еще раз перечислим, за что отвечают наши постулаты: 1. Система исчерпывающе описывается волновой функцией координат входящих в нее частиц и времени. 2. Изменения волновой функции во времени описываются уравнением Шредингера 3. Каждой наблюдаемой физической величине сопоставляется линейный самосопряженный оператор. Между операторами сохраняются те же отношения, что и между соответствующими величинами в классической механике. 4. При измерении физической величины F, с которой связан оператор F, будут наблюдаться лишь такие значения, которые совпадают с собственными значениями этого оператора. 5. Математическое ожидание (среднее значение) величины F для системы, находящейся в состоянии y, определяется интегралом
|
, то при измерении этой величины мы получим значение l, соответствующее собственному значению
или 
. Повторяя это измерение многократно (например, располагая сотней частиц в одном и том же состоянии), мы, конечно, будем каждый раз получать одно и то же точное значение измеряемого свойства.
соответствует спектр 
. Разложим y по собственным функциям 
: 
. Напомним, что эти функции ортонормированы. Тогда интеграл
, и величину | ck |2 можно интерпретировать как вероятность того, что при измерении будет получено значение ak. Отметим, что утверждение о том, что математическое ожидание 
величины А для системы в состоянии y составляет
коммутируют. Тогда собственные функции 
.
.
, то неопределенности Δ A и Δ B в величинах A и B удовлетворяют соотношению
– оператор умножения на константу, и 
, откуда следует знаменитое соотношение
.
.
, а потенциальная – 
.
.
,
,
.
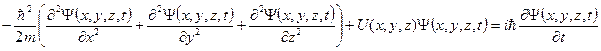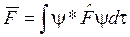