Доверительные интервалы для оценки числовых характеристик нормального распределенияДоверительный интервал для математического ожидания нормального распределения (при известном s)
В некоторых случаях среднее квадратическое отклонение s ошибки измерения (а вместе с нею и самого измерения) бывает известно. Например, если измерения проводились одним и тем же прибором при одних и тех же условиях, то s для всех измерений одно и тоже и обычно бывает известным. Пусть количественный признак Х генеральной совокупности распределен нормально с параметрами а и s, причем среднее квадратическое отклонение s известно. Требуется оценить неизвестное математическое ожидание а по выборочной средней Будем рассматривать
Т.4.1. Если СВ Х распределена нормально, то выборочная средняя
Пусть выполняется соотношение
где g - заданная надежность. Если в формуле (см. нормальное распределение)
заменить Х на
где Тогда Так как вероятность Р задана и равна g, то получим:
Смысл соотношения (3): С надежностью g можно утверждать, что доверительный интервал Число t определяется из равенства
Здесь Ф(t) – функция Лапласа, значение которой табулированы.
Доверительный интервал для математического ожидания нормального распределения (при неизвестном s) стр.291 Очевидно, в этом случае нельзя использовать ранее полученный интервал. Однако, по данным выборки можно построить СВ
которая имеет распределение Стьюдента с k = n – 1 степенями свободы. Здесь Пользуясь распределением Стьюдента, можно найти доверительный интервал
покрывающий неизвестный параметр а с надежностью g. Для значений tg существуют специальные таблицы, в которых по заданным n и g можно найти tg.
Доверительный интервал для среднего квадратического отклонения нормального распределения стр.292-293 Пусть количественный признак Х генеральной совокупности распределен нормально. Требуется оценить неизвестное генеральное среднее квадратическое отклонение s по «исправленному» выборочному среднему квадратическому отклонению s. Для этого построим доверительные интервалы, покрывающие параметр s с заданной надежностью g. Потребуем, чтобы выполнялось соотношение
где g - заданная надежность. Преобразуем неравенство |s – s| < e:
Таким образом, неравенство (4) примет вид:
Смысл соотношения (5): С надежностью g можно утверждать, что доверительный интервал (s(1-q); s(1+q)) покрывает неизвестный параметр s, причем точность оценки определяется как e = qs
Для q = q(g, n) составлены таблицы, по которым для известных n и g определяется q.
Замечание Выше предполагалось, что q < 1. Если q > 1, то, учитывая, что s > 0, получим
то есть доверительный интервал имеет вид (0; s(1+q)).
Заключение На сегодняшней лекции мы изучили задачу оценивания параметров известного теоретического распределения, познакомились с точечными и интервальными оценками, рассмотрели их свойства.
|

 . Для этого построим доверительные интервалы, покрывающие параметр а с надежностью g.
. Для этого построим доверительные интервалы, покрывающие параметр а с надежностью g. и выборочные значения признака x1, x2, …, xn – как одинаково распределенные независимые СВ X1, X2, …, Xn. При этом
и выборочные значения признака x1, x2, …, xn – как одинаково распределенные независимые СВ X1, X2, …, Xn. При этом  .
. .
. ,
,
 , то получим
, то получим ,
, . Отсюда
. Отсюда  .
. .
.
 (3)
(3) покрывает неизвестный параметр а, причем точность оценки определяется как
покрывает неизвестный параметр а, причем точность оценки определяется как  .
. Þ
Þ 
 ,
, , n – объем выборки.
, n – объем выборки. ,
,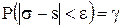 , (4)
, (4)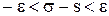
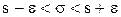
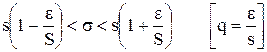

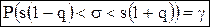 (5)
(5) ,
,


