Системы линейных уравнений
Системы линейных уравнений Систему m линейных уравнений с n неизвестными будем записывать в следующем виде:
Здесь x 1, x 2, ¼, xn – неизвестные величины, aij (i = 1,2, ¼, m; j = 1, 2, ¼, n) – числа, называемые коэффициентами системы (первый индекс фиксирует номер уравнения, второй — номер неизвестной), b 1, b 2, ¼, bm –числа, называемые свободными членами. Решением системы будем называть упорядоченный набор чисел x 1, x 2, ¼, xn, обращающий каждое уравнение системы в верное равенство. Решить систему — значит найти все ее решения или доказать, что ни одного решения нет. Система, имеющая решение, называется совместной. Если система имеет только одно решение, то она называется определенной. Система, имеющая более чем одно решение, называется неопределенной (совместной и неопределенной). Если система не имеет решений, то она называется несовместной. Система, у которой все свободные члены равны нулю, (b 1 = b 2 =¼ = bn = 0), называется однородной. Однородная система всегда совместна, так как набор из n нулей удовлетворяет любому уравнению такой системы. Если число уравнений системы совпадает с числом неизвестных (m=n), то система называется квадратной. Две системы, множества решений которых совпадают, называются эквивалентными или равносильными (совпадение множеств решений означает, что каждое решение первой системы является решением второй системы, и каждое решение второй системы является решением первой). Две несовместные системы считаются эквивалентными. Преобразование, применение которого превращает систему в новую систему, эквивалентную исходной, называется эквивалентным или равносильным преобразованием. Эквивалентными преобразованиями являются: а) умножение обеих частей уравнения на число, отличное от нуля, б) прибавление к одному уравнению другого уравнения. Очевидно, что прибавление к одному уравнению другого уравнения, умноженного на какое-либо число, также является эквивалентным преобразованием. Эквивалентность преобразований а) и б) читателю предлагается доказать самому. Также читателю предлагается доказать самому, что с помощью преобразований а) и б) можно получить новую систему, которая будет отличаться от исходной только тем, что в новой системе два любых уравнения исходной системы переставлены местами. Введём новое понятие. Прямоугольную таблицу, состоящую из p строк и q столбцов, будем называть матрицей размера p´q:
Числа aij называются элементами матрицы. Первый индекс фиксирует номер строки, а второй – номер столбца, где находится данный элемент. Если p = q, то есть число столбцов матрицы равно числу строк, то матрица называется квадратной. Элементы aii образуют главную диагональ матрицы. Матрицу будем обозначать заглавной латинской буквой. Две матрицы называются равными, если они одного размера и на одинаковых местах в них стоят одинаковые элементы. Матрица М называется нулевой матрицей (М = 0), если все её элементы равны нулю. Матрица
называется расширенной матрицей системы (1). Элементарными преобразованиями матрицы будем называть умножение всех элементов любой строки (или просто любой строки) на отличное от нуля число и прибавление ко всем элементам любой строки соответствующих (стоящих в том же столбце) элементов другой строки. Можно показать, что элементарными преобразованиями можно получить из данной матрицы, такую матрицу, у которой при сохранении всех остальных строк две строки поменяются местами. Очевидна справедливость утверждения: если к расширенной матрице некоторой системы уравнений I применить элементарное преобразование, то получится матрица, являющаяся расширенной матрицей системы II, эквивалентной системе I. Матрица (2) называется ступенчатой, если 1) ниже нулевой строки расположены только нулевые строки; 2) первый ненулевой элемент каждой строки равен 1; 3) если первый ненулевой элемент i -й строки расположен в столбце ji, то а) ji+ 1 > ji б) все элементы Матрица
является ступенчатой матрицей. Теорема 1. Каждая матрица конечным числом элементарных преобразований приводится к ступенчатому виду. Доказательство. Пусть матрица А имеет вид (2). Если А – нулевая матрица, то она имеет ступенчатый вид. Дальнейшее доказательство проведём по индукции по числу строк р. Если матрица состоит из одной строки, и в этой строке первый ненулевой элемент Для каждого i >; 1 вычтем из i -й строки первую строку, умноженную на Рассмотрим матрицу, получающуюся из матрицы А отбрасыванием первой строки. Эта матрица имеет р – 1 строку, и её первый столбец состоит из нулей. По индукции можно считать, что матрица В приведена к ступенчатому виду. Пусть в матрице В первые в строках ненулевые элементы расположены в столбцах с номерами Пусть матрица системы (1) приведена элементарными преобразованиями к ступенчатому виду. Полученная матрица является расширенной матрицей некоторой новой системы, эквивалентной исходной системе. Будем говорить, что новая система приведена к ступенчатому виду. Будем называть неизвестную xi базисной, если в некотором уравнении все коэффициенты при x 1, x 2,¼, xi- 1 равны нулю, а коэффициент при xi отличен от нуля (то есть, равен единице). Все остальные неизвестные назовём свободными. Если расширенная матрица системы уравнений приведена к ступенчатому виду, и последняя ненулевая строка этой матрицы имеет вид (0,0,0,¼,0,1), это значит, что система уравнений, эквивалентная исходной системе, содержит уравнение 0 х 1 + 0 х 2 + ¼0 хп = 1 (3) Очевидно, что это уравнение не имеет решения, откуда следует, что исходная система несовместна. Пусть в приведённой к ступенчатому виду расширенной матрице системы (1) нет строки вида (3). Предположим, что переменные х 1, х 2,¼, xr – базисные, а хr +1,¼, xn – свободные. Тогда преобразованная система имеет вид
|


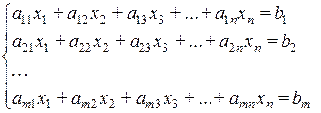 . (1)
. (1)
 (2)
(2) = 0 при всех k ¹ i.
= 0 при всех k ¹ i.
 , то поделив всю строку на
, то поделив всю строку на  . В новой матрице все коэффициенты
. В новой матрице все коэффициенты  .
. при условии
при условии  . Вычтем из первой строки вторую, умноженную на
. Вычтем из первой строки вторую, умноженную на  , третью строку, умноженную на
, третью строку, умноженную на  , и т. д. Таким образом, получим, что исходная матрица преобразована к ступенчатому виду, и теорема доказана.
, и т. д. Таким образом, получим, что исходная матрица преобразована к ступенчатому виду, и теорема доказана.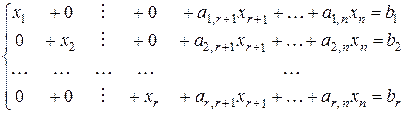 (4)
(4)


