Метод Ейлерадля студентів базових напрямів 6.170101 "Безпека інформаційних і комунікаційних систем", 6.170102 "Системи технічного захисту інформації", 6.170103 "Управління інформаційною безпекою"
Затверджено на засіданні кафедри «Безпека інформаційних технологій» Протокол № 12 від 12.05.2011р.
Львів – 2011
Укладачі: Л.В. Мороз, к.т.н., доц. А.Я. Горпенюк, к.т.н., доц. Н.М. Лужецька, асист.
Відповідальний за випуск: В.М. Максимович, д.т.н., проф.
Рецензент: В.В. Хома, д.т.н., проф. А.Е. Лагун, к.т.н., доц.,
ВСТУП Диференціальне рівняння (ДР), що містить лише одну незалежну змінну і похідні за нею, називають звичайними (ДР). ДР, що містить декілька незалежних змінних і похідні за ними, називають рівняння в частинних похідних. Порядком ДР називається найвищий порядок похідної (або диференціалу), який входить в рівняння. Звичайне ДР (ЗДР)
Диференціальне рівняння
Щоб розв’язати ЗДР, необхідно мати значення залежної змінної та (або) її похідних при деяких значення незалежної змінної. Якщо ці значення задані при одному значенні незалежної змінної - така задача називається задачею з початковими умовами або задачею Коші, а при Значення залежної змінної та її похідних називаються додатковими умовами, котрі в задачі Коші називаються початковими, а в крайовій задачі - граничними.
Задача Коші Задача Коші формулюється так: Нехай задане ДР
з початковими умовами
Положення нової точки визначають за нахилом кривої, обчисленому з допомогою ДР. Таким чином, графік чисельного розв’язку являє собою послідовність коротких прямолінійних відрізків, якими апроксимується істинна крива Існують дві групи методів розв’язування задачі Коші. 1. Однокрокові методи. В них для знаходження наступної точки на кривій 2. Багатокрокові. Для знаходження наступної точки кривої Всі ці методи розв’язування ДР дають розв’язок у вигляді таблиці значень.
Метод Ейлера Метод Ейлера є найпростішим методом розв’язування задачі Коші. Він дозволяє інтегрувати ДР першого порядку виду.
Метод Ейлера базується на розкладі функції
Якщо
Похідну
роблячи як завгодно багато кроків. Похибка методу має порядок Недолік методу Ейлера - нагромадження похибок, а також збільшення об’ємів обчислень при виборі малого кроку В методі Ейлера на всьому інтервалі
Модифікований метод Ейлера В модифікованому методі Ейлера спочатку обчислюється значення функції в наступній точці за звичайним методом Ейлера.
Воно використовується для обчислення наближеного значення похідної в кінці інтервалу Обчисливши середнє між цим значенням похідної та її значенням на початку інтервалу, знайдемо більш точне значення
В обчислювальній практиці використовується також метод Ейлера-Коші з ітераціями: 1) знаходиться грубе початкове наближення (за звичайним методом Ейлера)
2) будується ітераційний процес
Ітерації продовжують до тих пір, доки два послідовні наближення не співпадуть з заданою похибкою
Метод Рунге – Кутта четвертого порядку В методі Рунге-Кутта значення
Якщо розкласти функцію
Замість того, щоб обчислювати члени ряду за формулою (10) в методі Рунге-Кутта використовують наступні формули.
Похибка на кожному кроці має порядок Деколи зустрічається інша форма представлення методу Рунге-Кутта 4-го порядку точності.
Методи з автоматичною зміною кроку Застосовуються в тому випадку, якщо розв’язок потрібно одержати із заданою точністю. При високій точності (похибка
Метод Рунге-Кутта з автоматичною зміною кроку Після обчислення
Маємо
1) Якщо
обчислення повторюються з кроком 2) Якщо виконується ця умова, то можливі два варіанти, в залежності від значення K, де K – ознака поділу кроку. Початкове значення а) Якщо б) Якщо В обох випадках а) і б) результат
Метод Рунге-Кутта-Мерсона з автоматичною зміною кроку Метод дозволяє оцінити похибку на кожному кроці інтегрування. При цьому не потрібно зберігати в пам’яті обчислення значень функцій на кроці Алгоритм методу 1. Задаємо число рівнянь 2. За допомогою п’яти циклів з керуючою змінною
3. Знаходимо значення
та похибку 4. Перевіряємо виконання умов
Можливі випадки: а) Якщо перша умова не виконується, тобто б) Якщо виконується перша та друга умови, значення Якщо друга умова не виконується, крок Треба відмітити, що похибка
Метод Рунге-Кутта-Фельберга з автоматичною зміною кроку Це метод четвертого порядку, дає більш точну оцінку похибки (порівняно з методом Рунге-Кутта-Мерсона) на кожному кроці і реалізується послідовним циклічним обчисленням за наступними формулами:
Похибка
Якщо а) б) Якщо Час розрахунку для однієї точки удвічі більший, ніж для методу Рунге-Кутта-Мерсона. Методи прогнозу і корекції Дані методи для обчислення положення нової точки використовують інформацію про декілька раніше отриманих точок. Для цього застосовується дві так звані формули прогнозу і корекції. Схеми алгоритмів для таких методів приблизно однакові, а самі методи відрізняються лише формулами. Обчислення виконують таким чином. Спочатку за формулою прогнозу та початковими значеннями змінних визначають значення
знаходимо похідну:
Ця похідна підставляється у формулу корекції для обчислення уточненого значення
Якщо значення похідної недостатньо близьке до попереднього, то воно вводиться у формулу корекції і ітераційний процес продовжується. Якщо ж похідна змінюється в допустимих межах, то значення Метод Мілна На етапі прогнозу використовується формула Мілна.
а на етапі корекції - формула Сімпсона
Останні члени в обох формулах в ітераційному процесі не використовуються і служать лише для оцінки помилок. Метод Мілна відносять до методів четвертого порядку точності. Потрібно мати на увазі, що для користування формулою (11) необхідно попередньо одним із однокрокових методів визначити Похибка, внесена на будь-якому кроці, зростає експоненціально, тому методу Мілна властива нестійкість.
|

 -го порядку в загальному випадку має незалежну змінну, невідому функцію та її похідні до
-го порядку в загальному випадку має незалежну змінну, невідому функцію та її похідні до  (1)
(1) - незалежна змінна;
- незалежна змінна; - невідома функція (залежна змінна);
- невідома функція (залежна змінна); - похідні цієї функції.
- похідні цієї функції. (2)
(2) або більше значеннях незалежної змінної - задача називається крайовою.
або більше значеннях незалежної змінної - задача називається крайовою.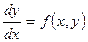 (3)
(3) . Потрібно знайти функцію
. Потрібно знайти функцію  , що задовольняє дане рівняння та початкову умову. Для одержання чисельний розв’язку цієї задачі спочатку обчислюють значення похідної, а потім задаючи малий приріст, переходять до нової точки
, що задовольняє дане рівняння та початкову умову. Для одержання чисельний розв’язку цієї задачі спочатку обчислюють значення похідної, а потім задаючи малий приріст, переходять до нової точки
 . Сам чисельний метод визначає порядок дій при переході від даної точки кривої до наступної.
. Сам чисельний метод визначає порядок дій при переході від даної точки кривої до наступної. вимагається інформація більш ніж про одну з попередніх точок.
вимагається інформація більш ніж про одну з попередніх точок. (4)
(4) в ряд Тейлора в околі точки
в ряд Тейлора в околі точки 

 (5)
(5) мале, то, знехтувавши членам розкладу, що містять в собі
мале, то, знехтувавши членам розкладу, що містять в собі  і т.д. отримаємо
і т.д. отримаємо (6)
(6) знаходимо з рівняння (4), підставивши в нього початкову умову. Таким чином можна знайти наближене значення залежної змінної при малому зміщенні
знаходимо з рівняння (4), підставивши в нього початкову умову. Таким чином можна знайти наближене значення залежної змінної при малому зміщенні  від початкової точки. Цей процес можна продовжувати, використовуючи співвідношення.
від початкової точки. Цей процес можна продовжувати, використовуючи співвідношення. ,
, , оскільки відкинуті члени, що містять
, оскільки відкинуті члени, що містять  . Очевидно, що це призводить до похибки, оскільки кути нахилу дотичної в точках
. Очевидно, що це призводить до похибки, оскільки кути нахилу дотичної в точках  та
та  різні. Точність методу можна підвищити, якщо покращити апроксимацію похідної.
різні. Точність методу можна підвищити, якщо покращити апроксимацію похідної. (7)
(7) .
. :
: (8)
(8)
 (9)
(9) . Якщо після декількох ітерацій співпадіння нема, то потрібно зменшити крок
. Якщо після декількох ітерацій співпадіння нема, то потрібно зменшити крок 

 функції
функції  , як і в методі Ейлера, визначається за формулою
, як і в методі Ейлера, визначається за формулою
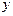 в ряд Тейлора і обмежитись членами до
в ряд Тейлора і обмежитись членами до  включно, то приріст
включно, то приріст  можна записати у вигляді
можна записати у вигляді (10)
(10)

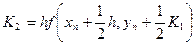


 . Таким чином метод Рунге-Кутта забезпечує значно вищу точність ніж метод Ейлера, однак вимагає більшого об’єму обчислень.
. Таким чином метод Рунге-Кутта забезпечує значно вищу точність ніж метод Ейлера, однак вимагає більшого об’єму обчислень.




 ) автоматична зміна кроку забезпечує зменшення загального числа кроків в декілька разів (особливо при розв’язках у вигляді кривих, що сильно відрізняються крутизною).
) автоматична зміна кроку забезпечує зменшення загального числа кроків в декілька разів (особливо при розв’язках у вигляді кривих, що сильно відрізняються крутизною). з кроком
з кроком 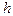 всі обчислення виконуються повторно з кроком
всі обчислення виконуються повторно з кроком  . Після цього порівнюються результати, отримані в точці хn+ 1 з кроком
. Після цього порівнюються результати, отримані в точці хn+ 1 з кроком 
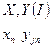
 - значення незалежної змінної в точці
- значення незалежної змінної в точці 
 - значення функції в точці
- значення функції в точці 
 - значення функції в точці
- значення функції в точці  , обчислене з кроком
, обчислене з кроком 
 - значення функції в точці
- значення функції в точці  , обчислене з кроком
, обчислене з кроком 
 - значення функції
- значення функції  , обчислене з кроком
, обчислене з кроком 
 і т.д., доки не виконається умова
і т.д., доки не виконається умова  .
. і залишається таким після першого поділу кроку на два. Надалі, якщо крок ділиться, то K приймає значення одиниці.
і залишається таким після першого поділу кроку на два. Надалі, якщо крок ділиться, то K приймає значення одиниці. , то навіть коли виконалась умова
, то навіть коли виконалась умова  , крок не змінюється, тобто лишається тим самим (обчислення далі проводяться з попереднім кроком).
, крок не змінюється, тобто лишається тим самим (обчислення далі проводяться з попереднім кроком). .
. виводиться на друк.
виводиться на друк.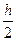 для оцінки похибки.
для оцінки похибки. , похибку
, похибку  , початковий крок інтегрування
, початковий крок інтегрування  , початкові умови
, початкові умови  .
. обчислюємо коефіцієнти
обчислюємо коефіцієнти




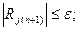 , то ділимо крок
, то ділимо крок  .
. та
та  виводяться на друк.
виводяться на друк. на кожному кроці методу Рунге-Кутта-Мерсона оцінюється приблизно. При розв’язуванні нелінійних ДР істинна похибка може відрізнятися в декілька разів від заданої
на кожному кроці методу Рунге-Кутта-Мерсона оцінюється приблизно. При розв’язуванні нелінійних ДР істинна похибка може відрізнятися в декілька разів від заданої  , де
, де  .
. - крок поділити на 2 і повернутися на початок.
- крок поділити на 2 і повернутися на початок. для всіх рівнянь: виводимо на друк
для всіх рівнянь: виводимо на друк  , а крок збільшуємо удвічі.
, а крок збільшуємо удвічі.







 , крок
, крок  зменшується в двічі
зменшується в двічі , крок
, крок  . Верхній індекс (0) означає, що прогнозоване значення є одним із послідовності значень уп +1, розташованих в порядку зростання точності. За прогнозованим значенням
. Верхній індекс (0) означає, що прогнозоване значення є одним із послідовності значень уп +1, розташованих в порядку зростання точності. За прогнозованим значенням 

 . В свою чергу
. В свою чергу  використовується для одержання більш точного значення похідної:
використовується для одержання більш точного значення похідної:
 використовується для обчислення остаточного значення
використовується для обчислення остаточного значення  . Після цього процес повторюється і обчислюється
. Після цього процес повторюється і обчислюється  .
. , (11)
, (11) (12)
(12) і значення похідних
і значення похідних  .
.


