Координатно-векторний метод розв’язування стереометричних задачВпровадження здоров'язберігаючих технологій потребує від учителя, по-перше, не допускати перевантаження учнів, визначаючи оптимальний обсяг навчальної інформації й способи її надання, враховувати інтелектуальні та фізіологічні особливості учнів, індивідуальні мовні особливості кожного учня. Намагатися планувати такі види роботи, які сприяють зниженню втоми. Здоров'язберігаючі технології передбачають: зміну видів діяльності, чергування інтелектуальної, емоційної, рухової видів діяльності; групової й парної форм роботи, які сприяють підвищенню рухової активності, вчать вмінню поважати думки інших, висловлювати власні думки, правилам спілкування; проведення ігор та ігрових ситуацій, нестандартних уроків, інтегрованих уроків. Вступ
Координатний метод розв'язування задач на сьогоднішній день найбільш потужний і при правильному підході дозволяє розв'язувати фактично всі види математичних, фізичних, астрономічних і технічних задач.
ТЕЗИ наукової роботи «Координатний метод розв'язування», Виконаної Гоменюком Владиславом Валентиновичем– учнем 9-Б класу Гімназії № 59 ім. О. М. Бойченка м. Києва, слухач МАН педагогічний керівник: Кабанець Тетяна Іванівна – Вчитель-методист гімназії №59 ім.О.М.Бойченка
В своїй роботі я поставив задачу показати, як розв'язуються стереометричні задачі, якщо на них поглянути «по-іншому», тобто розглянути задачу в тривимірній системі координат. Предметом дослідження є координатно-векторний метод розв’язування стереометричних задач.
Координатно-векторний метод розв’язування стереометричних задач Деякі метричні задачі зручно розв’язувати за допомогою координатно-векторного методу. Це перш за все завдання, в яких мова йде про куб, прямокутний паралелепіпед або тетраедр з прямим кутом. Прямокутна система координат у просторі природним чином пов'язана з многогранниками, при цьому серед координат їх вершин є багато нулів, що спрощує обчислення. Сутність координатного методу, як і векторного, полягає в тому, що геометрична задача перекладається на мову алгебри, і її розв’язання зводиться до розв’язання рівнянь, нерівностей чи їх систем. З курсу стереометрії відомо, що рівняння площини, що проходить через точку
Навпаки, будь-яке рівняння першого степеня Положення площини в просторі однозначно визначається заданням трьох точок, що не лежать на одній прямій. Нехай дана площина перетинає осі координат в точках
де числа
і рівняння
Отримане рівняння називають рівнянням площини у відрізках. Його часто застосовують при розв’язуванні задач. Як відомо, відстань між двома точками
Користуючись даною формулою можна легко вивести рівняння сфери. В прямокутній системі координат рівняння сфери радіуса R з центром в точці
Якщо центр сфери співпадає з початком координат, то рівняння матиме вигляд:
Розглянемо способи задання прямої в координатному просторі. Нехай пряма l проходить через дану точку Довільна точка
де t– деяке число (параметр). Дане співвідношення в координатах рівносильне системі рівнянь:
Дану систему називають параметричними рівняннями прямої. Якщо пряма l паралельна осі Нехай жодна з координат вектора
Отримані рівняння називаються канонічними рівняннями прямої. Виведемо формулу для обчислення відстані від даної точки
Нехай перпендикуляр, проведений з точки Тоді
Так як вектор
Позначимо
Виразимо скалярний добуток, що стоїть в знаменнику дробу, через координати векторів
Точка
Враховуючи, що
Отже, для того щоб обчислити відстань від точки Наведемо основні векторні співвідношення і формули, які використовуються для розв'язування стереометричних задач. 1) Для будь-яких трьох точок Α, Β,C має місце рівність:
2) Для будь-яких трьох точок Α, Β і О виконується рівність:
3) Для того, щоб точка С лежала на прямій АВ, необхідно і достатньо, щоб існувало таке число k, що
З даної рівності випливає, що
4) Нехай А і В – дві різні точки прямої і точка С – точка даної прямої така, що
де О – довільна точка. Відмітимо, що
тобто Нехай
Дану формулу називають формулою ділення відрізка в даному відношенні. Якщо С – середина відрізка АВ, то
5) Чотирикутник ABCD є паралелограмом тоді і тільки тоді, коли виконується одна з наступних рівностей:
де O – довільна точка простру. 6) Якщо вектори 7) В просторі для кожного вектора
(x, y, z – однозначно визначені числа). 8) Нехай точки А, В, С не лежать на одній прямій; тоді для того щоб точка D лежала в площині АВС, необхідно і достатньо, щоб існувала така пара чисел α і β, що При розв’язуванні різних геометричних задач на обчислення довжин відрізків і величин кутів, на доведення геометричних нерівностей ефективно використовувати скалярне множення векторів. Нагадаємо його основні властивості. 1) З визначення скалярного добутку слідує, що
тобто скалярний квадрат вектора рівний квадрату його довжини. Отже, для знаходження довжини відрізка AB може бути використана формула
За допомогою скалярного добутку двох векторів можна знаходити довжину відрізка, величину кута, отже, знаходити відстані, площі та інші метричні характеристики геометричних фігур. Для доведення перпендикулярності прямих і площин зручно користуватися ознакою перпендикулярності двох ненульових векторів: Для знаходження довжини відрізка АВ векторним способом в якості базисних вибирають такі вектори, довжини яких і кути між якими вже відомі. Потім записують розклад вектора
Якщо в задачі потрібно знайти величину кута
2) Для будь-яких векторів
3) Відрізки AB і CD перпендикулярні тоді і тільки тоді, коли
4) Для будь-яких векторів
Для успішного використання векторного методу, корисно знати деякі рівності, які часто використовуються для роз’язування задач. 5) Для будь-яких векторів
6) Для будь-яких трьох точок A, B і C:
теорема косинусів. 7) Для будь-яких чотирьох точок A, B, C, D:
Вектори
Доведена рівність є узагальненням рівності 6), яка випливає з неї при співпаданні точок D і A.
|

 перпендикулярно ненульовому вектору
перпендикулярно ненульовому вектору  в прямокутній системі координат має вигляд:
в прямокутній системі координат має вигляд: ,
, , де
, де 
 визначає в координатному просторі єдину площину, яка перпендикулярна вектору з координатами (A, B, C).
визначає в координатному просторі єдину площину, яка перпендикулярна вектору з координатами (A, B, C). ,
,  ,
,  , але не проходить через початок координат. Підставивши координати цих точок у загальне рівняння площини, отримаємо:
, але не проходить через початок координат. Підставивши координати цих точок у загальне рівняння площини, отримаємо: ,
,  ,
,  ,
, відмінні від нуля. Звідси знаходимо:
відмінні від нуля. Звідси знаходимо:
 приводиться до вигляду:
приводиться до вигляду:
 і
і  обчислюється за формулою:
обчислюється за формулою:
 має вигляд:
має вигляд:

 і паралельна ненульовому вектору
і паралельна ненульовому вектору  Вектор
Вектор  називають напрямним вектором прямої l (рис. 2).
називають напрямним вектором прямої l (рис. 2). належить прямій l тоді і тільки тоді, коли вектори
належить прямій l тоді і тільки тоді, коли вектори або
або 

 то вектор
то вектор  є напрямним вектором, і рівняння прямої прийме вигляд:
є напрямним вектором, і рівняння прямої прийме вигляд: 
 (координата z прийме довільне значення).
(координата z прийме довільне значення).
 , заданої в прямокутній системі координат рівнянням
, заданої в прямокутній системі координат рівнянням
 до площини
до площини  (Рис. 3).
(Рис. 3).
 перпендикулярний площині
перпендикулярний площині  то згідно з визначенням скалярного добутку,
то згідно з визначенням скалярного добутку,
 Тоді
Тоді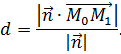
 і
і 
 лежить в площині
лежить в площині  . Таким чином, маємо:
. Таким чином, маємо:
 , отримаємо:
, отримаємо:
 до площини
до площини  замість
замість  підставити координати точки
підставити координати точки 
 (правило трикутника).
(правило трикутника). .
.
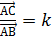 .
. . Доведемо істинність формули:
. Доведемо істинність формули:
 , інакше було б, що
, інакше було б, що 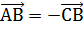 , або
, або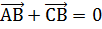 ,
, . Але це неможливо, тому що А і В різні точки.
. Але це неможливо, тому що А і В різні точки. Користуючись правилом віднімання векторів, отримаємо:
Користуючись правилом віднімання векторів, отримаємо: ,
, ,
,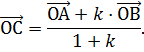
 і
і .
. ,
,  ,
,  ,
, неколінеарні, то для будь-якого вектора
неколінеарні, то для будь-якого вектора  , що лежить в одній площині з
, що лежить в одній площині з  .
. існує єдиний розклад за трьома некомпланарними векторами
існує єдиний розклад за трьома некомпланарними векторами 
 .
. ,
, .
.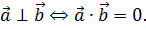
 за базисними векторами і знаходять:
за базисними векторами і знаходять:
 , то в якості базисних беруть вектори з відомими відношеннями їх довжин і кутами між ними. Потім вибирають вектори
, то в якості базисних беруть вектори з відомими відношеннями їх довжин і кутами між ними. Потім вибирають вектори  на сторонах цього кута з початком в його вершині і розкладають їх по базису, після чого знаходять cos φ за формулою
на сторонах цього кута з початком в його вершині і розкладають їх по базису, після чого знаходять cos φ за формулою
 .
. .
.
 .
. ,
, .
. і
і  в лівій частині представимо у вигляді різниці двох векторів, відкладених від точки A. Отримаємо:
в лівій частині представимо у вигляді різниці двох векторів, відкладених від точки A. Отримаємо: .
.


