Видоизмененная частотная характеристика
W*(jw) = Re[Wлч (jw)] + jwIm[Wлч (jw)]
Определим выражение для комплексного коэффициента передачи линейной части системы. Wлч (jw) =
Тогда видоизмененная частотная характеристика
W*(jw) =
Подставляя числовые данные получим: W*(jw) =
Расчетные данные занесем в таблицу и строим график (рис. 34.)
Рис. 34
tg(α) = В / а2 = 1/1 = 1 = К1.
Точка А, характеризующая Гурвицев угол, в который должна вписываться нелинейность, соответствует координате А(-1/К1, 0). Если через эту точку можно провести прямую так, чтобы видоизмененная частотная характеристика вся лежала справа от нее, то система абсолютно устойчива. В нашем случае это сделать невозможно. Т.к. W*(jw) пересекает отрицательный отрезок вещественной оси при значении Re(w)=–5.8, то можно вычислить критическое значение коэффициента К = tg a, ограничивающее Гурвицев угол (рис. 35.).
Рис. 35
Если нелинейность впишется в угол, образованный осью ОХ и линией 0,172х=y, то САУ будет устойчива. В нашем случае нелинейность не вписывается в этот угол, значит, при заданной нелинейности и заданных параметрах линейной части она абсолютно неустойчива.
Задача №2
Построить фазовый портрет системы.
Рис. 36
Уравнение свободного движения для ошибки в соответствии со структурной схемой имеет следующий вид:
В соответствии с нелинейной характеристикой, y(e) = В×sign [e(t)], уравнение свободного движения можно записать для двух областей, разделенных линиями переключения, т.е. когда y(e) = + В и y(e)= – В. Особенностью фазовых портретов систем, содержащих нелинейные элементы с кусочно-линейной статической характеристикой является то, что фазовые траектории можно построить для отдельных областей, на которые фазовая плоскость будет разделена линиями переключения. Линии переключения соответствуют точкам излома статической характеристики НЭ. Для каждой области будет свое уравнение фазовой траектории, смена уравнений происходит на линии переключения. Таким образом, задавшись некоторыми начальными условиями, строят фазовую траекторию по уравнению соответствующей области, дойдя до линии переключения, решение приостанавливают – определяют координаты точки на линии переключения. Эти координаты являются начальными условиями для уравнения фазовой траектории после линии переключения. Этот метод называют методом «сшивания решений». Уравнение НЭ
Для нашего типа НЭ линия переключения – ломаная.
Рис. 37
Для области справа от линии переключения y(e)=+В и уравнение
Для области слева от линии переключения y(e)= - В и уравнение
Запишем эти уравнения в форме Коши, введя координаты состояния e=х1.
Запишем дифференциальное уравнение второго порядка в форме Коши:
e=x1.
Для области справа от Для области слева от линии переключения линии переключения
Исключим из уравнений время, поделив второе уравнение на первое:
Разделяя переменные и интегрируя, получим уравнения фазовых траекторий для двух областей фазовой плоскости.
В этих уравнениях x1 – ошибка, а х2 – скорость ее изменения, с - произвольная постоянная интегрирования, которая определяется начальным положением изображающей точки. Так как нам надо построить фазовый портрет, то начальные условия произвольны и поэтому -:< c <:. Подставим в эти уравнения численные значения: (1) (2) Задаваясь значениями скорости изменения ошибки
Таблица №1
Таблица №2
По фазовому портрету видно, что все фазовые траектории стягиваются к предельному циклу. Это значит, что в системе устанавливается режим устойчивых автоколебаний, амплитуда которых определяется по оси х (абсцисса предельного цикла), а частота по оси ординат Если нелинейный элемент имеет зону нечувствительности или линейную область (усилитель с ограничением), то фазовая плоскость разбивается на три области. Две области, аналогичные рассмотренным выше и описываемые теми же уравнениями, а третья, где y(e)=0 – для зоны нечувствительности, и y(e)=КНЭ ×e - для линейной зоны усилителя с насыщением. Подставив эти значения в уравнения для интегрирования, получим уравнение фазовой траектории для третьей области. Линии переключения соответствуют точкам излома нелинейной характеристики (рис.39).
Рис. 38
Рис. 39
Для НЭ 3 в области III фазовые траектории можно построить методом изоклин или более простым – методом Льенара.
Задача №3 Исследовать динамику нелинейной САУ. Определить режимы и параметры автоколебаний при изменении К системы заданной следующей структурной схемой (рис. 40):
Рис. 40
Параметры линейной части: К=50; Т1=15 с; Т2=1 с; Т3=5 с; Т4=1 с, Параметры нелинейного элемента: В=1; а=2.
Проведя гармоническую линеаризацию нелинейного элемента, получаем комплексную частотную функцию НЭ.
Как видим из уравнения, она зависит от А – амплитуды на входе НЭ и не зависит от w. Для определения наличия и параметров автоколебаний используют уравнение характеристического вектора:
Это уравнение можно решить аналитически (в простых случаях) или графически – построив АФЧХ линейной части по выражению WЛЧ(jw) при 0<w<: и инверсную отрицательную характеристику НЭ (в одном масштабе). Точка пересечения этих графиков дает решение уравнения и позволяет определить wАК по АФЧХ и ААК – по инверсной характеристике нелинейного элемента. При таком типе НЭ автоколебания возникают при неустойчивой линейной части. Запишем уравнение характеристического вектора
Так как, по заданию, Т2=Т4, то выражение упрощается и приводится к виду:
Найдем аналитическое решение, выделив в полученном уравнении вещественную и мнимую части и приравняв их нулю. Получим два уравнения с двумя неизвестными wАК и ААК. Если будет найдено положительное вещественное решение, то оно соответствует режиму автоколебаний с параметрами wАК и ААК, если такого решения нет – то автоколебания не возникают.
Из второго уравнения выражаем частоту
Т.о. частота определяется только постоянными времени. Подставив выражение для w2 в первое уравнение
где К – коэффициент усиления линейной части, как видно из этого уравнения амплитуда автоколебаний будет зависеть от k. Подставим численные значения:
Решив его, найдем значение ААК.
Исследуем влияние k на амплитуду автоколебаний.
При к= 10:
ААК=47,6 При к= 20 ААК=95,6. При к= 30 ААК=142,8.
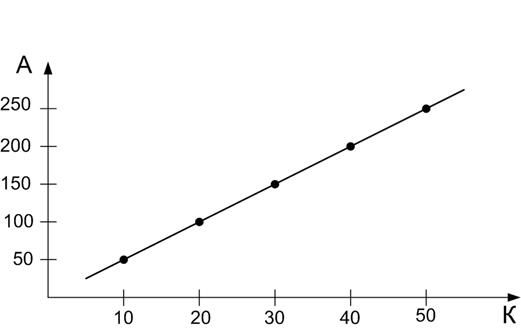
Таким образом, по уравнению, ААК=f(К) – нелинейная функция. Построим график этой зависимости (рис. 41).
Рис. 41
По этому графику можно определить какая, будет ААК при определенном значении К. В случае, если аналитическое решение затруднено, можно решить уравнение характеристического вектора графически. Для этого построим АФЧХ системы и
Для НЭ без зоны неоднозначности АФЧХ можно полностью не строить, а определить значение |W(jw)| на частоте, при которой j(w)=-180°. Запишем уравнение фазочастотной характеристики j(w)= - 90 – arctg wT1 – arctg wT3 = - 90 – arctg 15w - arctg 5w = - 180 ® w=0,115 при ½j½=180° Найдем значение модуля АФЧХ на этой частоте
Рассчитаем инверсную отрицательную характеристику НЭ, задаваясь значениями А (А>a)
Приравнивая
Для упрощения можно воспользоваться графиком Если строить полностью АФЧХ линейной части, то также можно использовать полярную систему координат, рассчитывая модуль и фазовый сдвиг для различных частот, из наших расчетов видно, что диапазон можно сузить 0 < w < 1, т.к. при w=0,115 j(w)=-180. А нас интересует пересечение АФЧХ с отрицательным отрезком вещественной оси. Для К =50
АФЧХ и Таким образом, в нашей системе при 10 £ K £ 50 (в соответствии с рисунком) возникает режим автоколебаний и увеличение К приводит к увеличению амплитуды. Колебания исчезнут, если сделать линейную часть устойчивой. Определим при каком К линейная часть устойчива. Запишем характеристическое уравнение линейной части:
Т.о. при k <0,26 линейная часть будет устойчива, а при k= 0,267 – пройдет через точку с координатой (-1; 0j) ® ½W(jw)½=1, а график
Рис. 42
Задача №4 Рассчитать устойчивость и переходной процесс импульсной системы.
Для определения устойчивости и расчета переходной характеристики надо записать передаточную функцию приведенной непрерывной части системы, которая включает непрерывную часть и формирователь импульсов (в импульсной системе) или ЦАП (экстраполятор нулевого порядка) – в цифровой.
Т – период дискретности.
где H(p) – изображение Лапласа переходной функции. Следовательно, можно найти h(t) по H(p) – изображению, а затем найти z-преобразование для функции времени. Можно найти таблицы перехода от H(p) к z-преобразованию, т.е. H(z), не находя h(t). Например, раскладываем на простые слагаемые:
Коэффициенты A, B, C, D – определяются приравниванием числителя и коэффициента К.
Найдя передаточную функцию приведенной непрерывной части в z-форме, нужно найти z-передаточную функцию системы в замкнутом состоянии.
Тогда z-изображение переходной функции равно произведению WЗАМ(z) на z-изображение 1-ой ступенчатой функции, т.е. 1(t) ®x(t)
По характеристическому уравнению в z-форме можно оценить устойчивость.
Все корни z-уравнения по модулю должны быть меньше единицы в устойчивой системе. Переход оси z-изображения переходной функции к оригиналу h(nT), t=nT – дискретное время, выполняется по обратному преобразованию (g - интегрирование вдоль окружности единичного радиуса r)
Найти ординаты h(t) в дискретные моменты можно делением полинома числителя H(z) на полином знаменателя. Конечное значение h[nT]|h®: можно определить, используя теорему о пределах:
Если система устойчива, предел существует. Например, для структурной схемы:
По таблицам переходим от преобразования Лапласа к z-преобразованию.
Обозначим
Найдем Wзам:
Запишем изображение переходной характеристики:
Пусть К=2, Т1=1с, Т=0,1с.
е-0,1=0,9048, тогда
Характеристическое уравнение системы:
Корни по модулю меньше единицы – система устойчива.
h[nT] – получаем делением полинома числителя H(z) на полином знаменателя, записав изображение для отрицательных степеней z (т.е. поделив почленно числитель и знаменатель на z2).
Результаты деления дают ординаты переходной характеристики в дискретные моменты (n – определяет степень при z)
Время счета – дискретное –
Рис. 43
Литература
|

 =
=  =
= – j
– j  = Re(w) – jIm(w).
= Re(w) – jIm(w). – j
– j  = Re*(w) – j Im*(w)
= Re*(w) – j Im*(w) - j
- j 


 ,
,  .
.
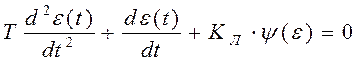 .
.

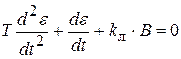

 , тогда
, тогда .
.

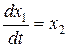 ,
,





 - для области справа от линии переключения (обл. I);
- для области справа от линии переключения (обл. I);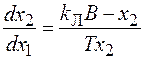 - для области слева от линии переключения (обл. II).
- для области слева от линии переключения (обл. II). - табличный интеграл.
- табличный интеграл. - для области I;
- для области I; - для области II.
- для области II. ;
; .
.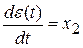 и различными значениями с рассчитаем
и различными значениями с рассчитаем 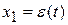 . Расчеты по обоим уравнениям сводим в таблицы №1 и №2, затем по этим данным в плоскости x1(e(t)) и
. Расчеты по обоим уравнениям сводим в таблицы №1 и №2, затем по этим данным в плоскости x1(e(t)) и  - по оси ординат строим фазовые траектории. Удобнее всего рассчитать значения х 1, задаваясь х 2 при с =0, построить фазовую траекторию, а затем определить какие с i целесообразнее брать. Фазовый портрет для рассмотренного примера приведен на рисунке 38
- по оси ординат строим фазовые траектории. Удобнее всего рассчитать значения х 1, задаваясь х 2 при с =0, построить фазовую траекторию, а затем определить какие с i целесообразнее брать. Фазовый портрет для рассмотренного примера приведен на рисунке 38



 для А>а.
для А>а. ,
,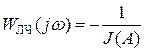 .
.



 ®
®  ®
® 
 ,
, .
. ,
,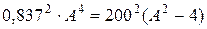 ,
, ,
, .
. ,
, ,
, ,
, ®
®  ,
, ,
, ,
,
 ,
, .
.
 .
.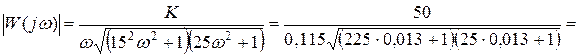



 определим амплитуду автоколебаний. При К =50
определим амплитуду автоколебаний. При К =50
 ® AАК=239,6
® AАК=239,6 .
.
 ,
, ,
, ®
®  .
. начинается с отметки -3,14, при А=0, значит они не пересекутся, следовательно, автоколебаний нет.
начинается с отметки -3,14, при А=0, значит они не пересекутся, следовательно, автоколебаний нет.
 - в изображениях Лапласа,
- в изображениях Лапласа, ,
, 


 .
. .
.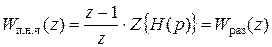 ,
, .
. ,
, .
. .
. .
. .
.
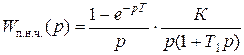 ; z=epT;
; z=epT; .
.
 .
.

 .
.
 .
.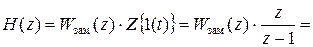
 .
. .
.

 .
. .
.

 .
. ,
,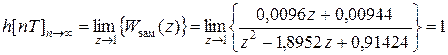 .
. .
.




