V. Коэффициент интенсивности напряжений (КИН).V. Коэффициент интенсивности напряжений (КИН). 1. Поля напряжений и перемещений в окрестности вершины трещины. 2. Частные случаи определения КИН. 3. Численные методы определения КИН. 4. Определение НДС в вершине трещины для анизотропного случая.
1. Поля напряжений и перемещений в окрестности вершины трещины.
Рис. 1. – Тело с трещиной.
Заменим реальную трещину математическим разрезом (Рис. 2), решение задачи удобно рассматривать в полярных координатах (центр координат в вершине трещины).
Рис. 2. – Математическая модель тела с трещиной.
Аналитические решения могут быть получены с помощью методов функций комплексного переменного. Решение в явном виде задачи теории упругости по определению напряженно-деформированного состояния вблизи вершины трещины существует для трех типов простых трещин. В полученных решениях для перехода от плоского-напряженного состояния к плоско-деформированному состоянию нужно сделать замену:
I. Для трещины нормального отрыва (тип I) решение имеет следующий вид:
II. Для трещины поперечного сдвига (тип II):
III. Для трещины продольного сдвига (тип III):
Величины, характеризующие изменение напряженно-деформированного состояния в вершине трещины, зависящие от геометрии образца и внешних нагрузок, называются коэффициентом интенсивности напряжений соответственно для трещины нормального отрыва (I тип), поперечного (II тип) и продольного (III тип) сдвига. При радиусе, стремящемся к нулю, ненулевые компоненты тензора напряжений стремятся к бесконечности
2. Частные случаи определения КИН.
Задача определения КИН с математической точки зрения не менее сложная, чем задача определения НДС. В настоящее время имеются только несколько аналитических решений для наиболее простых видов трещин (см. справочники по механике разрушений). Остальные частные случаи получены с помощью различных приближенных методов. Рассмотрим несколько частных случаев, конфигурации которых наиболее часто встречаются в технике и широко используются в инженерных расчетах. I.Трещина нормального отрыва в бесконечной плоскости нагруженная на бесконечности растягивающим усилием
Формула (5.5) носит название – «решение Ирвина». Если образец имеет ограничения по внешним размерам, то вводят поправку –
II. Краевая трещина в полубесконечной плоскости (Рис.3, Б):
IV. Краевая трещина в бесконечной полосе (Рис. 3, В):
здесь b – ширина полосы, l – длина трещины. Формула (5.8) – «решение Гросса». В реальных задачах полоса имеет конечные размеры. Если V. Центральная трещина в бесконечной полосе (Рис. 3, Г):
формула (5.10) с учетом условия (5.9) носит название «решения Ирвина».
формулы (5.11) –«решение Федерсена».
формула (5.12) – «решение Исиды».
Рис. 3. – Виды трещин: А) Трещина нормального отрыва; Б) Краевая трещина в полубесконечной плоскости; В) Краевая трещина в бесконечной полосе; Г) Центральная трещина в бесконечной полосе.
V. Бесконечная полоса с двумя краевыми трещинами (Рис. 4, А):
VI. Круглая трещина в массиве (Рис. 4, Б):
где VII. Бесконечная плоскость с трещиной поперечного сдвига (Рис. 4, В):
VIII. Бесконечная плоскость с трещиной продольного сдвига, нагрузка перпендикулярна листу (Рис. 4, Г):
   
В Г Рис. 4. – Виды трещин: А) Бесконечная полоса с двумя краевыми трещинами; Б) Круглая трещина в массиве; В) Бесконечная плоскость с трещиной продольного сдвига; Г) Бесконечная плоскость с трещиной поперечного сдвига.
IX. Трещина в бесконечной анизотропной плоскости (Рис. 5, А):
X. Асимметричное расклинивающее усилие в плоскости под произвольным углом (Рис. 5, Б). Суперпозиция трех видов трещин.
где
а б Рис. 5. – Виды трещин: А) Трещина в бесконечной анизотропной плоскости; Б) Плоская трещина с произвольным усилием, сосредоточенным на берегах трещины.
Задача определения НДС в простейшем случае сводится к следующему: из справочника берется частное решение наиболее близкое к реальному, из него находится КИН, а затем найденное значение подставляем в асимптотические формулы (5.2 – 5.4).
3. Численные методы определения КИН.
Аналитические решения задач для тел с трещиной получены только для некоторых частных случаев, они сведены в таблицу. Поэтому при решении большинства реальных задач для оценки НДС и КИН используют численные методы. Метод конечных элементов. Условно разделяют на прямые и энергетические методы определения КИН. Прямые методы. Один из основных методов (асимптотические методы) основан на использовании асимптотических формул и заключается в следующем: с использованием любого численного метода определяется НДС вблизи вершины трещины; затем в формулу (5.20) подставляются значения тензора напряжений
Преимущества: возможность использования стандартных процедур и программ. Недостатки: погрешность решения зависит от погрешности конечно-элементной аппроксимации, т.е. необходимо мелкое разбиение в вершине трещины; коэффициент интенсивности характеризует скорость изменения напряжений, поэтому нужно рассматривать точку как можно ближе к вершине трещины, вследствие чего получаем большую погрешности численного решения. Пути повышения точности решения: использование мелких сеток; поэтапное решение задачи с постепенным сгущением сетки в вершине трещины; использование сингулярных конечных элементов. Энергетические методы. Данные методы определения КИН основываются на использовании зависимости коэффициента интенсивности напряжений от изменения потенциальной энергии упругого деформирования
для плоско-напряженного состояния, в случае плоско-деформированного состояния значение «приведенного» модуля Юнга вычисляется по формуле (5.22):
Метод податливости (метод полной энергии). В изотермических задачах теории упругости изменение потенциальной энергии упругого деформирования
В методе конечных элементов это реализуется по следующей схеме:
где
В матричном виде:
где Порядок решения задачи: В силу симметрии можно рассматривать половину тела с трещиной. Трещина в МКЭ задается свободной поверхностью (узлы не закреплены). Приращение длины трещины
Рис. 6. – Конечно-элементная модель тела с трещиной.
Для выбранной конечно-элементной сетки (Рис. 6); при длине трещины Преимущества метода: использование одной и той же конечно-элементной сетки исключает систематическую ошибку. Возможность использования грубого разбиения, за исключением области вершины трещины, где задается приращение длины трещины. Недостатки: можно использовать только там, где справедливо соотношение (5.21), справедливо только для плоских случаев (трещин), в основном на модельных задачах. Метод виртуального роста трещины. Приращение роста трещины задается смещением узла (Рис. 7).
Рис. 7. – Схема смещения узла КЭ сетки.
Меняется геометрия – меняется и матрица жесткости.
Дифференцирование матрицы сводится к вычислению приращений (их отношения).
Метод граничных элементов (Рис. 8). С помощью любого МГЭ (по аналогии с МКЭ) можно определить НДС и с использованием сингулярных формул либо других зависимостей определить КИН. В качестве граничного элемента выступает трещина. Метод разрывных смещений. В данном методе постановка физической и математической задачи совпадают. Следовательно, для оценки НДС этот метод является одним из наиболее предпочтительных,
Рис. 8. – Граничный элемент. где
Решение задачи теории упругости имеет вид:
Рассмотрим пример:
Рис. 9. – Тело с трещиной, нагруженное внутренним давлением.
На бесконечности:
Разделим трещину на
Если разрыв смещений имеет место на отрезке
где Напряжение в центре
Согласно принципу суперпозиции, напряжение в центре
где
Численное решение задачи о трещине под действием внутреннего давления определяется из решения системы с
Эти уравнения можно решить относительно
4. Определение НДС для анизотропного случая. Уравнения теории упругости для ортотропного материала:
Для обобщенного плоско-напряженного состояния:
Для обобщенного плоско-деформированного состояния:
Для ПДС закон Гука для ортотропной среды можно записать в следующем виде (исключив
где коэффициенты
Можно записать коэффициенты
где Таким образом, заменяя технические постоянные Рассмотрим решение для ортотропного тела с трещиной. Дифференциальное уравнение (5.51) для плоской задачи теории упругости (для ортотропного материала) впервые было получено Лехницким:
где Введем оператор
Тогда основное уравнение относительно
где
Уравнение Лехницкого (5.51) может быть использовано для задачи определения НДС для бесконечной ортотропной среды с трещинами различного типа. Решение для трещины нормального отрыва (5.54) имеет вид:
Для трещины поперечного сдвига (5.55):
Для трещины продольного сдвига (5.56):
где Анализ решений: – для анизотропного и для изотропного случаев в решении присутствует сингулярность по напряжениям, ее порядок – ½. Это следствие того, что решение получено по теории упругости (материал работает только в упругой области) и в вершине напряжения стремятся к бесконечности; – в анизотропном случае (в отличие от изотропного) решение зависит не только от КИН и координат, но и от упругих характеристик материала.
|

 Ставится задача вычисления напряженно-деформированного состояния вблизи вершины трещины. Данная задача сводится к решению плоской задачи теории упругости для математического разреза с граничными условиями, реализующими один из типов трещин. Рассмотрим тело с трещиной (Рис. 1), выберем систему координат с центром в вершине трещины.
Ставится задача вычисления напряженно-деформированного состояния вблизи вершины трещины. Данная задача сводится к решению плоской задачи теории упругости для математического разреза с граничными условиями, реализующими один из типов трещин. Рассмотрим тело с трещиной (Рис. 1), выберем систему координат с центром в вершине трещины.

 (5.1)
(5.1) ;
; ;
; ;
;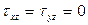 ,
,  ; (5.2)
; (5.2) ;
; .
.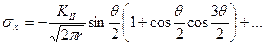 ;
; ;
;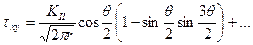 ;
; ;
; .
. ;
;  ;
; ;
;  ; (5.4)
; (5.4) .
. . Это является следствием решения задачи в упругой постановке. Поля напряжений и деформаций вблизи трещины для каждого вида трещины отличаются только на величину КИН (коэффициент интенсивности напряжений).
. Это является следствием решения задачи в упругой постановке. Поля напряжений и деформаций вблизи трещины для каждого вида трещины отличаются только на величину КИН (коэффициент интенсивности напряжений). (Рис. 3, А).
(Рис. 3, А). (5.5)
(5.5) , которая называется “ К -тарировка”- коэффициент учитывающий форму, внешние размеры образца и характер расположения трещины:
, которая называется “ К -тарировка”- коэффициент учитывающий форму, внешние размеры образца и характер расположения трещины: (5.6)
(5.6) (5.7) формула (5.7) – «решение Бови».
(5.7) формула (5.7) – «решение Бови». , где (5.8)
, где (5.8) ,
,  , (5.9)
, (5.9) , то используем «решение Гросса»; иначе необходимо учитывать величину
, то используем «решение Гросса»; иначе необходимо учитывать величину  (длину полосы).
(длину полосы). (5.10)
(5.10) ,
, 
 ,
,  (5.11)
(5.11) ,
,  (5.12)
(5.12)
 – «решение Бови». (5.13)
– «решение Бови». (5.13) – «решение Ирвина». (5.14)
– «решение Ирвина». (5.14) , (5.15)
, (5.15) - радиус трещины. Формула (5.15) – «решение Снеддона».
- радиус трещины. Формула (5.15) – «решение Снеддона». . (5.16)
. (5.16) . (5.17)
. (5.17)

 А Б
А Б

 ;
; ; (5.18)
; (5.18) .
. ;
; ; (5.19)
; (5.19) ,
, - расстояние от оси симметрии до точки, в которой сосредоточено произвольное усилие.
- расстояние от оси симметрии до точки, в которой сосредоточено произвольное усилие.

 и определяется
и определяется  .
. ;
;  ;
; ;
;  . (5.20)
. (5.20) формула (5.21).
формула (5.21).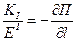 ; (5.21)
; (5.21) . (5.22)
. (5.22) равно работе внешних сил
равно работе внешних сил  (5.23).
(5.23). . (5.23)
. (5.23) ; (5.24)
; (5.24) ; (5.25)
; (5.25) , (5.26)
, (5.26) -м индексом обозначены узлы в которых приложена внешняя нагрузка.
-м индексом обозначены узлы в которых приложена внешняя нагрузка. ,
,  (5.27)
(5.27) ; (5.28)
; (5.28) , (5.29)
, (5.29)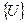 ,
,  - узловые усилия и перемещения.
- узловые усилия и перемещения. моделируется высвобождением узла перед вершиной трещины.
моделируется высвобождением узла перед вершиной трещины.







 и заданной внешней нагрузки решается задача теории упругости (определяем НДС). Находим матрицы узловых перемещений
и заданной внешней нагрузки решается задача теории упругости (определяем НДС). Находим матрицы узловых перемещений  . На этой же сетке конечных элементов и при той же нагрузке, но при длине трещины (
. На этой же сетке конечных элементов и при той же нагрузке, но при длине трещины ( ) решаем задачу нахождения матрицы узловых перемещений
) решаем задачу нахождения матрицы узловых перемещений  . Найденные величины подставляем в формулу (5.29) и определяем КИН.
. Найденные величины подставляем в формулу (5.29) и определяем КИН. 
 (5.30)
(5.30) (5.31)
(5.31)
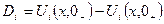 – разрыв смещений. (5.32)
– разрыв смещений. (5.32) (5.33)
(5.33) (5.34)
(5.34)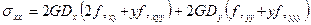 (5.35)
(5.35) (5.36)
(5.36) (5.37)
(5.37)
 Трещина нормального отрыва в бесконечной плоскости под действием внутреннего давления
Трещина нормального отрыва в бесконечной плоскости под действием внутреннего давления  (Рис. 9).
(Рис. 9).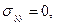
 ,
,  ;
;
 ;
;
 . (5.38)
. (5.38)
 .
. отрезков (граничных элементов). Предположим, что граничные элементы настолько малы, что разрыв смещения в направлении оси y в пределах каждого элемента можно считать постоянным. Нормальное напряжение
отрезков (граничных элементов). Предположим, что граничные элементы настолько малы, что разрыв смещения в направлении оси y в пределах каждого элемента можно считать постоянным. Нормальное напряжение  в точке
в точке  , вызванное постоянным вдоль отрезка
, вызванное постоянным вдоль отрезка  разрывом смещения
разрывом смещения  равно (5.39):
равно (5.39): . (5.39)
. (5.39) с центром в точке
с центром в точке  , то значение нормального напряжения
, то значение нормального напряжения  будет вычислено по формуле (5.40):
будет вычислено по формуле (5.40): , (5.40)
, (5.40) – разрыв смещений на отрезке
– разрыв смещений на отрезке  .
. -ом элементе, находится путем подстановки
-ом элементе, находится путем подстановки  вместо
вместо  :
: . (5.41)
. (5.41)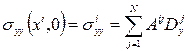 , (5.42)
, (5.42) – коэффициенты влияния, находятся по формуле (3.43):
– коэффициенты влияния, находятся по формуле (3.43): . (5.43)
. (5.43) . (5.44)
. (5.44) (Рис. 10):
(Рис. 10):

 ;
; ; (5.45)
; (5.45) ;
; ;
;  ;
;  .
.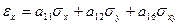 ;
; ;
;  .
. ;
;  ;
;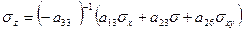 . (5.47)
. (5.47) ):
): ;
; ; (5.48)
; (5.48) ,
, описываются формулами (5.49):
описываются формулами (5.49): ;
; ;
; ; (5.49)
; (5.49)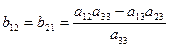 ;
; ;
; .
. ;
;  ;
; ;
;  , (5.50)
, (5.50) ,
,  ,
,  ,
,  ,
, 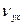 – эффективные упругие характеристики.
– эффективные упругие характеристики. на
на  , (5.51)
, (5.51) функция Эри.
функция Эри. (
( ):
): . (5.52)
. (5.52) запишется в форме:
запишется в форме: ,
, - корни характеристического уравнения (комплексно-сопряженые величины) в научной литературе
- корни характеристического уравнения (комплексно-сопряженые величины) в научной литературе 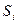 ,;
,; 
 - действительные числа:
- действительные числа: ;
; ; (5.53)
; (5.53) .
.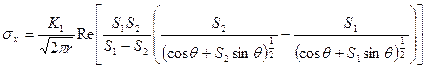 ;
; ;
; ;
; ;
; ;
; ; (5,54)
; (5,54) ;
; ;
; .
. ;
; ;
; ;
; ; (5.55)
; (5.55) .
. ;
; ; (5.56)
; (5.56)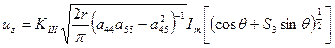 ,
, – действительная часть от комплексного числа,
– действительная часть от комплексного числа,  – мнимая часть от комплексного числа.
– мнимая часть от комплексного числа.


