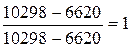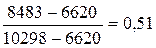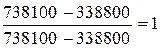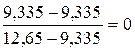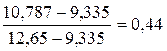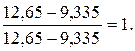Производственной программы предприятия
Найти план, удовлетворяющий следующим условиям: Хi ³ 0 (1) Хi – целое число (2)
Хi £ Вj или Хi ³ Вj (4) f1 (Х) = f2 (Х) = f3 (Х) = Неравенство (1) указывает на не отрицательность целочисленной переменной. Выражение (2) отражает требование получения целочисленного результата решения. Неравенство (3) отражает требование не превышения суммарного объема выпуска однородных в конструктивно-технологическом отношении изделий в течение планового периода (года) (если таковые имеются). Неравенства (4) предусматривают введения индивидуальных ограничений на объемы выпуска конкретных изделий. Целевая функция (5) характеризует требование максимизации объема валовой прибыли. Целевая функция (6) характеризует требование максимизации объема реализации готовой продукции. Целевая функция (7) характеризует требование максимизации доли завоевываемого целевого рынка. Для реализации приведенной выше экономико-математической модели необходимо располагать соответствующими исходными данными.
5. ИСХОДНЫЕ ДАННЫЕ ДЛЯ РЕШЕНИЯ ЗАДАЧИ
Состав необходимых исходных данных представляется по формам, приведенным в табл. 1 и 2.
Таблица 1 Экономические показатели по различным изделиям, выступающие в роли критериев оптимальности
Таблица 2 Ограничения, накладываемые рынком, на возможные объемы выпуска изделий годовой производственной программы по нашему иллюстративному примеру
Допустим, что нашему иллюстративному варианту соответствуют следующие необходимые для расчетов исходные данные, приведенные в табл. 3. Таблица 3
Студент самостоятельно устанавливает аналогичные исходные данные, приведенные в табл. 2-3. При этом они не должны полностью (в точности) копировать приведенные выше исходные данные. Допустимым считается то, что номенклатура изделий не должна быть меньше шести наименований (больше возможно). В тех случаях, когда не будет удаваться получать на ПЭВМ на первой итерации результата решения задачи (из-за отсутствия условия сходимости), студент самостоятельно корректирует исходные данные. Путем последовательных корректировок он добивается необходимого результата решения, при котором соблюдается условие сходимости. О достижении условия сходимости будет сообщать сама ПЭВМ в процессе решения задачи. Иначе говоря, информацию о получении или неполучении итогового решения сообщает сам компьютер в ходе реализации задачи.
6. ОПИСАНИЕ ПОРЯДКА РАБОТЫ НА ПЭВМ
1. Запускаем приложение Microsoft Excel 8.0. На экране монитора появится пустая электронная таблица Книги 1. 2. Сначала заполняется экранная таблица 4 применительно к критерию валовой прибыли. Данные второй графы табл. у всех вариантов одинаковые. На предварительном этапе расчетов объемы выпуска по всем изделиям принимаются равными 100 (они выступают в качестве опорного плана). Данные третьей графы (т.е. прибыль на 1 изделие) берутся из выбранного студентом варианта (см. табл. 3 графа 2 исходных данных). Таблица 4
Знак * – означает умножение. Экранная форма изображения табл. 4 выглядит следующим образом.
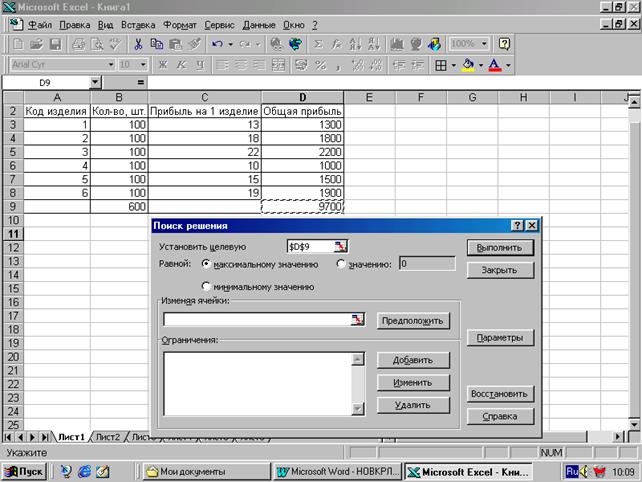
Информация в ячейке D9 получается следующим образом. Выделим ячейки с D3 по D9. Щелкнем мышью на значке S на панели инструментов. Автоматически появится число 9700 в ячейке D9. 3. Вызвать функцию "Поиск решения": А) Открыть на панели инструментов пункт меню "Сервис"; Б) активизировать (выполнить) команду «Поиск решения». На экране монитора появится диалоговое окно "Поиск решения". См. ниже.
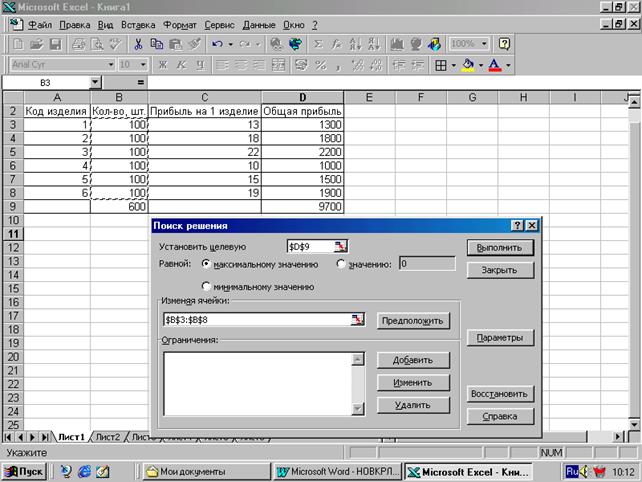
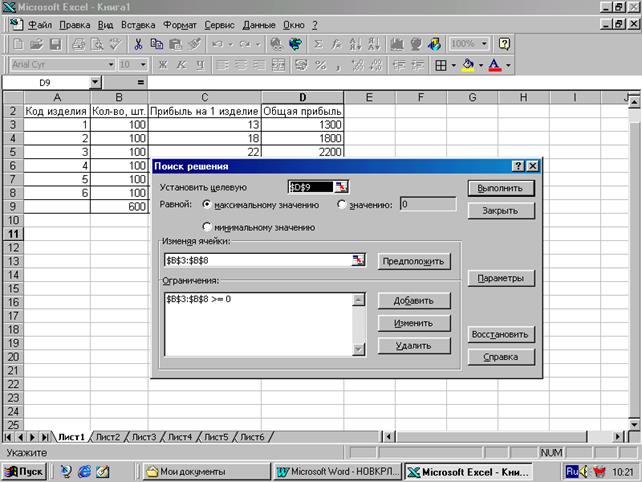
4. В поле "Установить целевую ячейку" надо ввести значение ячейки, в которой находится формула, предусматривающая расчет максимального объема валовой прибыли. В нашем случае это ячейка D9. Для этого установите курсор внутрь поля "Установить целевую ячейку". Затем установите указатель мыши на ячейку D9, нажмите левую кнопку мыши. Ее значение автоматически появится в поле "Установить целевую ячейку". 5. Установите указатель на нужный значок: Равной: - максимальному значению; - минимальному значению. В нашем случае надо активизировать значок, соответствующий "максимальному значению", так как целевая функция показателей (критериев) максимизируется. 6. В поле "Изменяя ячейки" укажите интервал ячеек, в которых хранятся данные о количестве выпускаемых изделий. В нашем случае это интервал В3-В8 согласно экранной формы табл. 4. (т.е. на экране монитора). Для этого поместите курсор мыши внутрь поля "Изменяя ячейки". Затем выделите интервал мышью (указатель мыши поместить на первую ячейку интервала – В3, нажмите левую кнопку мыши и удерживая ее протяните по всем ячейкам интервала до ячейки В8, отпустите кнопку мыши).
7. В поле "Ограничения" надо ввести поочередно все ограничения задачи, используя следующую последовательность действий:
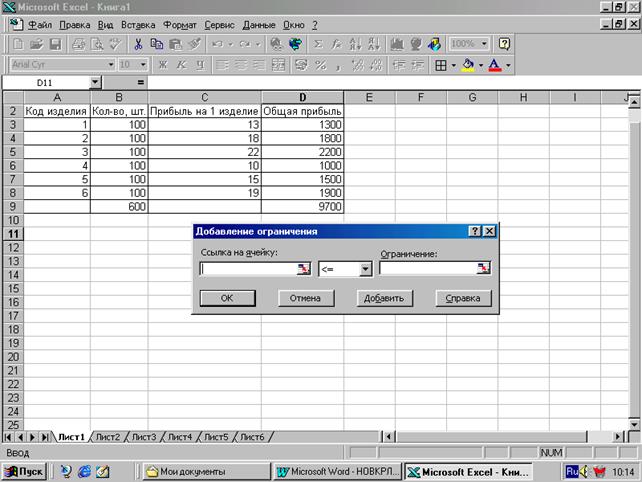
А) Нажать кнопку ДОБАВИТЬ. На экране появится диалоговое окно «Добавить ограничения». См. ниже.
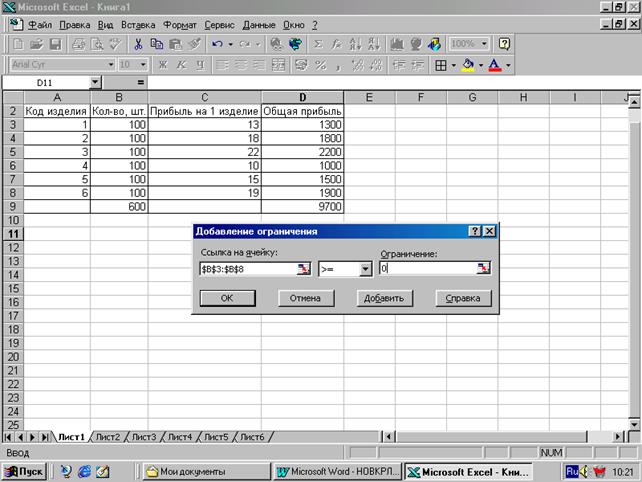
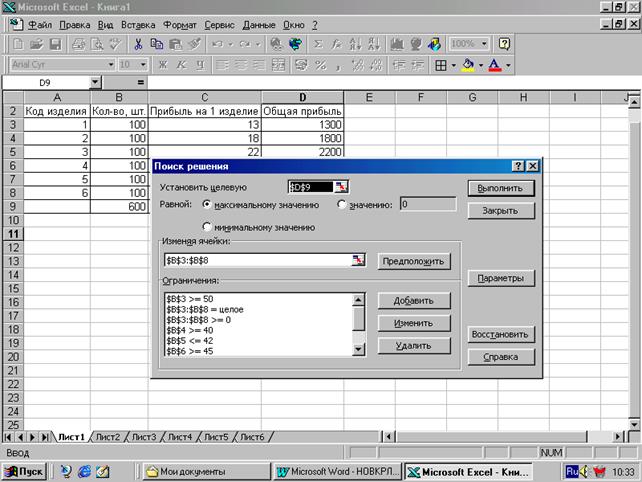
Б) В поле "Ссылка на ячейку" ввести соответствующую ячейку, для которой находятся значения ограничений правой части неравенств (выражений) модели задачи; В) Открыть список знаков уравнения и выбрать нужное; Г) В поле "Ограничение" ввести конкретное число. Например, нам нужно показать, что все изделия ³ 0. Для этого помещаем курсов в ячейку В2 и протягиваем до ячейки В8. В результате получим:
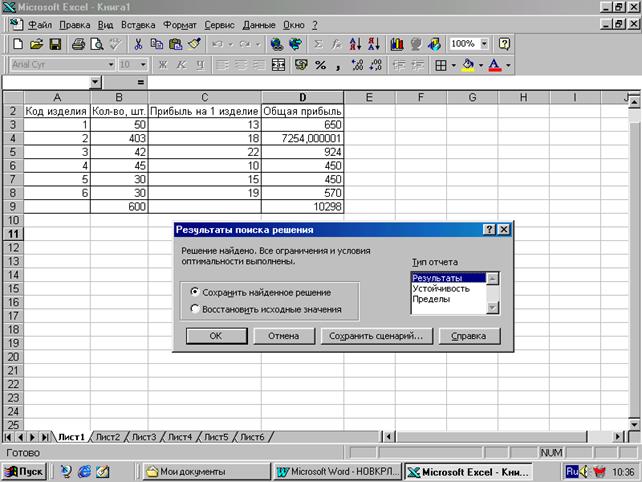
8. Нажать кнопку "ВЫПОЛНИТЬ". Появится окно:
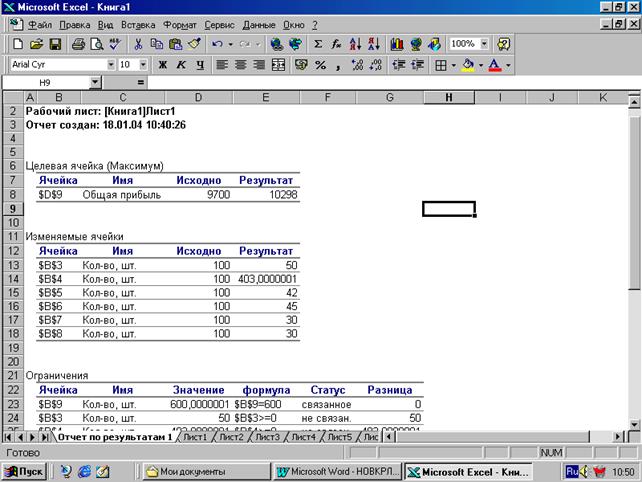
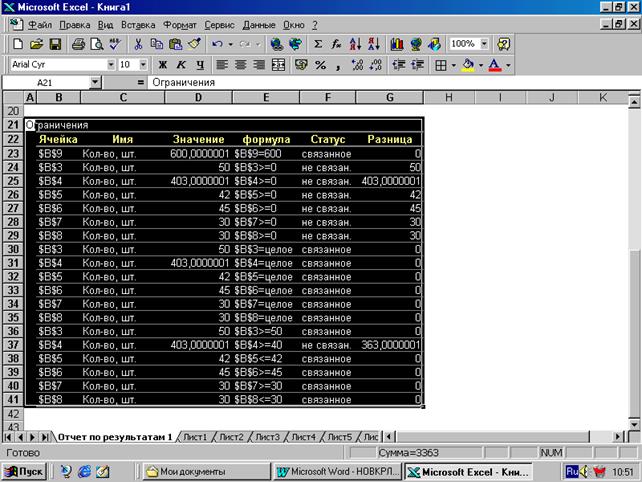
9. Указать ТИП ОТЧЕТА. В нашем случае это: "РЕЗУЛЬТАТЫ". Активизируем СОХРАНИТЬ НАЙДЕННОЕ РЕШЕНИЕ. Нажимаем на ОК. В итоге получает решение, которое заноситься в ячейки В3-В8 (т. е. на место прежней информации, содержащейся в табл. 4). Результат см. в вышеприведенной электронной табл. Далее выводится на печать сам ОТЧЕТ ПО РЕЗУЛЬТАТАМ:
В отчете по курсовой работе должны быть приведены все продемонстрированные выше формы экселевских таблиц хотя бы по одному варианту решения задачи (на выбор студента) В результате решения задачи по остальным двум критериям получим информацию о запланированных объемах выпуска изделий по трем альтернативным вариантам (см. табл. 5)
Для того чтобы определить по альтернативным вариантам численные значения соответствующих им критериев оптимальности по результатам решения, необходимо обратиться к исходным данным табл. 5. Таблица 5
По каждому из трех полученных вариантов решения задачи рассчитаем числовые значения по соответствующим (трем) критериям оптимальности. Вариант 1 – критерий - максимизация прибыли. Общая по плану прибыль составит: 50х13+403х18+42х22+45х10+30х15+30х19 = 10298 руб. Общий по плану объем реализации составит: 50х1300+403х20+42х1600+45х1200+30х1000+30х1400 = 338800 руб. Общая доля завоеванного рынка составит: 50х0,019+403х0,015+42х0,010+45х0,022+30х0,018+30х0,013 = 9,335 Вариант 2 – максимизация объема реализованной продукции Общая по плану прибыль составит: 413х13+40х18+42х22+45х10+30х15+30х19 =8483 руб. Общий по плану объем реализации составит: 413х1300+40х20+42х1600+45х1200+30х1000+30х1400 = 738100 Общая доля завоеванного рынка составит: 413х0,019+40х0,015+42х0,010+45х0,022+30х0,018+30х0,013 = 10,787
Аналогичным образом выполняются расчеты по третьему альтернативному варианту. После выполнения соответствующих расчетов получим результаты, которые сведем в табл. 6. Таблица 6 Численные значения различных критериев оптимальности по трем альтернативным вариантам решения задачи формирования производственной программы предприятия
Как видим, варианта решения задачи по различным критериям существенно различаются. Если не отдать безусловное предпочтение какому-либо критерию оптимальности экономико-математической модели, то возникает необходимость использования многоцелевого подхода с целью выбора оптимального варианта. Для приобретения практических навыков выбора наилучшего варианта решения задачи с помощью методов многокритериальной оптимизации воспользуемся рядом математических методов, достаточно широко применяемых на практике. Сначала надо привести разные по природе и единицам измерения численные значения критериев оптимальности к безразмерным величинам. Для этого необходимо воспользоваться формулой: fj = где
исследуемого критерия оптимальности. По первому критерию нормализованные значения по каждому из трех вариантов составят: J=1 J=2 J=3 По второму критерию нормализованные значения по каждому из трех вариантов составят: J=1 J=2 J=3 По третьему критерию нормализованные значения по каждому из трех вариантов составят: J=1 J=2 J=3 В сводном виде таблица нормализованных значений критериев по трем вариантам будет выглядеть так:
Решим задачу несколькими методами многокритериальной оптимизации.
|

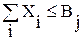 (3)
(3) max (5)
max (5)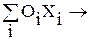 max (6)
max (6)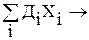 max (7)
max (7)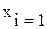 ³ 50
³ 50
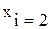 ³ 40
³ 40
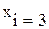 £ 42
£ 42
 ³ 45
³ 45
 ³ 30
³ 30
 £ 30
£ 30



 ,
,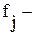 нормализованное значение критерия по соответствующему варианту решения задачи формирования годового плана предприятия;
нормализованное значение критерия по соответствующему варианту решения задачи формирования годового плана предприятия;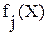 - текущее значение соответствующего критерия оптимальности по рассматриваемому варианту;
- текущее значение соответствующего критерия оптимальности по рассматриваемому варианту;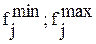 - соответственно минимальное и максимальное значение
- соответственно минимальное и максимальное значение