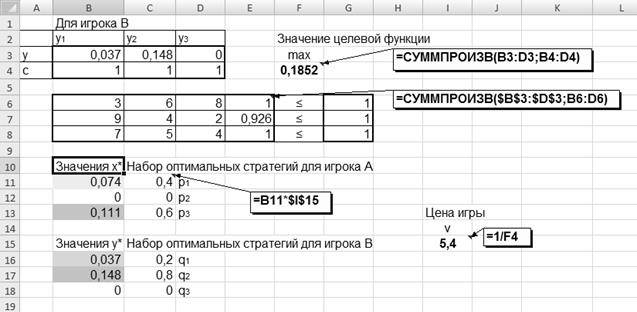
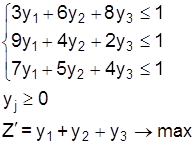Платежная матрица игры
Определить оптимальные пропорции в выпускаемой продукции, гарантирующие среднюю величину прибыли при любом состоянии спроса, считая его неопределенным. Решение. Задача сводится к игровой модели, в которой игра предприятия А против спроса В задана платежной матрицей (табл. 5.3). Определим нижнюю и верхнюю цены игры в табл. 5.2. Так как α ≠ β, то седловая точка отсутствует, и оптимальное решение следует искать в смешанных стратегиях игроков:
Обозначив xi = pi/v, yj = qj/v, составим две взаимно-двойственные задачи линейного программирования.
Рекомендуется решать задачу на максимум, как, например, задача 2, поскольку первое базисное решение для нее будет допустимым. Введем добавочные переменные и перейдем к уравнениям, т. е. приведём задачу линейного программирования к каноническому виду[1]. Учитывая соответствие между переменными задач (вторая теорема двойственности), получим:
т. е.: x* = (0,074; 0; 0,111), у* = (0,037; 0,148; 0). При решении задачи линейного программирования с помощью надстройки MS Excel «Поиск решения» решение двойственной задачи содержится в отчёте Устойчивость: основные переменные – в столбце «Результ. значение», а дополнительные – в столбце «Теневая цена». Используя первую теорему двойственности, получим: Zmin = Z´max = 0,185. По формуле (5.3): ν = 1/0,185 = 5,4. Учитывая, что xi = pi/v, yj = qj/v, получим: pi = xi ∙ v, p1 = 0,074 ∙ 5,4 = 0,4, p2 = 0 ∙ 5,4 = 0, p3 = 0,111 ∙ 5,4 = 0,6. qj = yj ∙ v, q1 = 0,037 ∙ 5,4 = 0,2, q2 = 0,148 ∙ 5,4 = 0,8, q3 = 0. Оптимальная стратегия игрока А – SA = (0,4; 0; 0,6), игрока В – SВ = = (0,2; 0,8; 0). Решение двойственной задачи линейного программирования представлено на рис. 5.1–5.3.
Рис. 5.1. Решение задачи теории игр с помощью надстройки MS Excel «Поиск решения»
Рис. 5.2. Данные для решения задачи в надстройке MS Excel «Поиск решения»
Рис. 5.3 Использование отчёта «Устойчивость» для поиска дополнительных переменных
Ответ: Предприятие должно выпустить 40 % продукции А1 и 60 % продукции А3, а продукцию А2 не выпускать. Оптимальный спрос в 20 % времени находится в состоянии В1, и в 80 % – в состоянии В2, при этом математическое ожидание прибыли составит 5,4 ден. ед. При решении произвольной конечной игры размера m × n рекомендуется придерживаться следующей схемы. 1. Исключить из платежной матрицы заведомо невыгодные стратегии по сравнению с другими стратегиями. Такими стратегиями для игрока А (игрока В) являются те, которым соответствуют строки (столбцы) с элементами, заведомо меньшими (большими) по сравнению с элементами других строк (столбцов). 2. Определить верхнюю и нижнюю цены игры и проверить, имеет ли игра седловую точку. Если седловая точка есть, то соответствующие ей стратегии игроков будут оптимальными, а цена совпадает с верхней (нижней) ценой. 3. Если седловая точка отсутствует, то решение следует искать в смешанных стратегиях.
5.5. Исходные данные
Методика решения задач по теории игр включает следующие этапы: 1) составление платёжной матрицы игры в соответствии с выбранными вариантами; 2) определение верхней и нижней цены игры; 3) если α ≠ β, то следует составить две взаимно-двойственные задачи; 4) решение задачи линейного программирования. Рекомендуется решать задачу на максимизацию целевой функции с ограничениями «меньше либо равно»; 5) формулирование выводов по задаче. Задача 1. Предположим, что ОАО «РЖД» осуществляет только три вида деятельности: грузовые перевозки; пассажирские перевозки в дальнем следовании; пассажирские перевозки в пригородном сообщении: (А1, A2 и А3) – стратегии игрока А, получая при этом прибыль, зависящую от спроса, который может быть в одном из четырёх состояний (В1, В2, В3 и В4) – стратегии игрока В. Определить оптимальные пропорции в видах деятельности, гарантирующие среднюю величину прибыли при любом состоянии спроса, считая его неопределенным. Игровая модель задаётся платежной матрицей с элементами аij, характеризующими прибыль, которую получит ОАО «РЖД» при выпуске i-й продукции с j-м состоянием спроса. Указания. Вывод сделать по образцу: «Следовательно, ОАО "РЖД" должно осуществлять виды деятельности в следующих пропорциях __ % грузовые перевозки – А1, __ % пассажирские перевозки в дальнем следовании – А2, а, допустим (условный пример!), пассажирские перевозки в пригородном сообщении – А3 не осуществлять. Оптимальный спрос в __ % времени находится в состоянии В1, и в __ % – в состоянии В2» и т. д. Задачи линейного программирования необходимо решать с помощью надстройки MS Excel «Поиск решения». Выбор вариантов. Стратегия игрока В имеет четыре стратегии – их оценки остаются неизменными. Для стратегия игрока А выбираются три стратегии по трём последним цифрам номера зачётной книжки. Например, три последние цифры зачётной книжки студента равны 285, таким образом, выбираем строки 2, 8, 5. Если три последние цифры номера зачётной книжки содержат два одинаковых числа, например, 055, то выбираются строки 0, 5, *(1) – одно совпадение (табл. 5.4); если номер содержит три одинаковые цифры, например, 555, то выбираются строки 5, *(1), **(1) – два совпадения (табл. 5.4). В случае, если платежная матрица содержит седловую точку, то строка, её содержащая, заменяется на значения строки ***(с.т.). Например, три последние цифры номера зачётной книжки 026, таким образом, платёжная матрица выглядит следующим образом (табл. 5.3). Таблица 5.3 Платёжная матрица игры по варианту 026
Поскольку α = β = 5, то имеется седловая точка; игра имеет решение в чистых стратегиях. Заменяем строку с набором стратегий А2 на строку ***(с.т.).
Таблица 5.4 Варианты для решения задачи по теории игр
В задаче следует привести доказательство существования (α = β) или отсутствия (α ≠ β) седловой точки (см. табл. 5.3).
& Рекомендуемая литература: [1, 2, 4, 6, 9, 11].
|

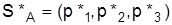 и
и 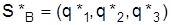 .
.