В информационной цепиИдентифицирующая информация или преобразование для установления тождества – это такая информация, которая относится к наименьшему возможному числу информации, необходимых для идентификации отдельного сообщения информационной цепи. Такие информации следует отличать от описательных информации, которые предназначены для описания определённого сообщения [2]. В разд. 2.2 и 2.3 отмечалось, что идентификация как процесс установления тождества осуществляется путём выбора, отыскания некоторого заданного сообщения (предмета, объекта, явления) из множества других сообщений. При этом считается, что у системы, осуществляющей такой поиск, имеется эталон искомого сообщения, т.е. имеется полное его описание, позволяющее отличить данное сообщение от других сообщений. Найти или выбрать сообщение – это значит указать где оно находится или когда появилось, или где и когда оно имеет место, или каков его номер в ряду других сообщений. Таким образом, критериями выделения сообщения могут быть пространство, время, пространство-время, а также порядок следования. Наличие эталона искомого сообщения обеспечивает возможность проверки выполнения условий, требуемых одним из установленных критериев. При выборе, выделении, идентификации сообщений делается только различие между тривиальной и нетривиальной информацией независимо от того, с помощью каких преобразований получена нетривиальная информация. Поясним это утверждение примером. Пусть информационная цепь со стоит из четырёх сообщений: < x 1, x 2, x 3, x 4>;, из которых под определённым углом зрения необходимо выделять сообщение х 2. В соответствии с теоремой 2.1 для описания произвольного сообщения этой информационной цепи требуются четыре описательные информации, которые связывают данные сообщения с исходным сообщением х 0:
J 01 x 0 = x 1, J 02 x 0 = x 2, J 03 x 0 = x 3, J 04 x 0 = x 4. При идентификации в качестве исходного сообщения берётся именно искомое сообщение, точнее говоря, его эталон, т.е. в нашем примере х 0 = x 2. При этом одна из рассмотренных информации будет тривиальной, а остальные нетривиальными:
J 21 x 2 = x 1, J°x 2 = x 2, J 23 x 2 = x 3, J 24 x 2 = x4.
Таким образом, видно, что идентификация некоторого сообщения основана на утверждении, что среди описательных информации есть тривиальная. Для этого необходимо найти ответы на следующие вопросы:
J 21 = J°?, J 22 = J°?, J 23 = J°?, J 24 = J°?
В результате ответов, которые имеют вид «да» или «нет», будут получены следующие четыре описательные информации: J 21 ≠ J°, J 22 = J°, J 23 ≠ J°, J 24 ≠ J° или x 2 ≠ x 1, x 2 = x 2, x 2 ≠ x 3, x 2 ≠ x 4. Из нашего примера видно, что число возможных описательных информации выделенного сообщения зависит от порядка задания вопроса, так как тривиальная информация в наилучшем случае может быть найдена после первого же вопроса, в наихудшем случае – после третьего, а при наличии n сообщений – после (n - 1)-го вопроса. В последнем случае n -й вопрос не нужен, так как очевидно, что это будет тривиальная информация. Рассмотрим условия, при которых число описательных информаций, необходимых для идентификации сообщений, не зависит от порядка следования вопросов. Это и будут идентифицирующие информации. Число информаций, идентифицирующих одно сообщение, будем обозначать символом Н. Теорема 2.4. Число описательных информаций, необходимых для идентификации сообщения, однозначно определено только в информационной цепи из двух сообщений; при этом Н 2 = 1. Данное утверждение доказывается тем, что в такой информационной цепи мы избавлены от случайности в порядке выбора сообщений, так как любой ответ на первый же вопрос – либо о наличии тривиальной информации, либо о выявлении нетривиальной описательной информации (в этом случае, очевидно, что тривиальной информацией является вторая) – позволяет однозначно выделить искомое сообщение. Таким образом, самая первая выявленная описательная информация, является информацией, идентифицирующей выделенное сообщение, т.е. Н 2 = 1. Число же описательных информаций здесь равно D 2 = 2. Одна из них – тривиальная информация, утверждающая, что описанное сообщение является выделенным сообщением, а вторая – нетривиальная – утверждает, что остальные сообщения не являются выделенными. Однозначностью выбора объясняется рассмотренный в разд. 1.5, 2.2, 2.3 известный способ идентификации (дихотомическая процедура), основанный на последовательном делении выбранного множества на две равные части с выбором одной из них и т.д. на каждом шаге вплоть до идентификации пары сообщений и выделением в ней искомого сообщения. Теорема 2.5. Число информаций, идентифицирующих одно сообщение в информационной цепи, содержащей n различных сообщений, может быть определено как двоичный логарифм этого числа сообщений. Докажем теорему. Дана информационная цепь из n сообщений, являющаяся половиной информационной цепи из 2 n сообщений. В соответствии с теоремой 2.1 числа информации, описывающих одно сообщение в этих информационных цепях соответственно равны: D n = n, D 2n = 2 n, вследствие чего D 2n = 2· D n. (2.24) Пусть число информаций, идентифицирующих одно сообщение в информационной цепи из n сообщений, равно H n. В соответствии с теоремой 2.4 для идентификации самой этой цепи, как одной из двух составляющих информационную цепь из 2 n сообщений, необходима одна идентифицирующая информация. Поэтому общее число информации, идентифицирующих данное сообщение в информационной цепи из 2 n сообщений, равно H 2n = H n + 1 (2. 25) Связь между H и D можно найти, прологарифмировав (2. 24) по основанию 2,
log2 D 2n = log22 D n = log2 D + log22
или log2 D 2n = log2 D n + 1. (2. 26) Из сравнения (2.25) и (2.26) следует, что на основании одной из них может быть найдена другая, если зависимость H=f (D) имеет вид H = log2 D. (2. 27) Для D n = n уравнение (3.27) приобретает вид H n = log2 n, (2. 28) т.е. идентично формуле (2.2) для определения количества информации аддитивной мерой Хартли. Заметим, что формулой Хартли (2.2) мы пользовались безотносительно к числу описательных информации D, однако, она справедлива лишь для частного случая, когда D = n; в более общих ситуациях, когда D ≤ n, справедливо уравнение Н = log2 D. Так как для идентификации одного из двух подмножеств множества сообщений требуется одна идентифицирующая информация, то число идентифицирующих информации H n равно числу последовательных разбиений множества на два равных подмножества, необходимых для идентификации сообщения из целой информационной цепи. Это совпадает с тем, что в разд. 2.2 мы назвали длиной программы или количеством информации для выбора сообщения. Теорема 2.6. Если в информационной цепи из n сообщений имеется m классов, каждый из которых состоит соответственно из n a, n b, …, n m одинаковых сообщений, то среднее число идентифицирующих информации можно выразить соотношением:
Докажем теорему. Считается данным, что в информационной цепи имеется:
…………………………………………
причём
В соответствии с теоремой 2.5 число информаций, идентифицирующих сообщение a 1 в информационной цепи из n сообщений, составляет
Аналогично находится число идентифицирующих информации, приходящихся на каждое сообщение остальных классов:
т.е.
Среднее количество информаций, идентифицирующих отдельное сообщение, можно определить средним значением чисел идентифицирующих информаций сообщений всех классов
откуда с учётом (2.29) получаем
или то же в компактном виде
где j – номер класса сообщения, m – число классов. В частном случае, когда все сообщения, информационной цепи различны, т.е. когда каждый класс представлен всего одним сообщением и m = n, из (2.32) имеем Теорема 2.7. Среднее число идентифицирующих информаций равно двоичному логарифму среднего числа описательных информации. Данное утверждение доказывается сравнением (2.20) и (2.32), из которого следует, что
Для усвоения фундаментального характера полученной формулы полезно ещё раз обратить внимание на замечание к формулам (2.27) и (2.28). Из уравнения (2.33) видно, что число идентифицирующих информаций Н меньше числа описательных информации D. Это объясняется тем, что описание одного сообщения из множества сообщений является также описанием всех сообщений данного множества, в то время как идентификация одного сообщения лишь означает утверждение, что ни одно из остальных сообщений не является искомым сообщением, т.е. при идентификации утверждается только то, что кроме одной тривиальной информации, все остальные нетривиальны без указания какими именно являются нетривиальные информации. При большом числе сообщений в информационной цепи, когда n → ∞, частоты появления сообщений разных классов можно заменить вероятностями этих сообщений [8]:
После подстановки (2.34) в (2.20) выражение для среднего количества описательных информации примет вид
где j – номер класса сообщения, m – число классов. Выражение (2.32) для среднего количества идентифицирующих информаций после аналогичной подстановки преобразуется к виду
Данное выражение, кроме того, может быть получено логарифмированием по основанию 2 зависимости (2.35) и является идентичным формуле (2.11), предложенной К. Шенноном для измерения количества информации.
|

 .
. сообщений
сообщений 
 сообщений
сообщений 
 сообщений
сообщений 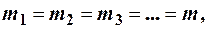
 .
. а число информации, «идентифицирующих» это же сообщение внутри своего класса, состоящего из n a сообщений, составляет
а число информации, «идентифицирующих» это же сообщение внутри своего класса, состоящего из n a сообщений, составляет  Но выделить сообщение a 1 внутри своего класса невозможно, так как сообщения
Но выделить сообщение a 1 внутри своего класса невозможно, так как сообщения  неразличимы из-за того, что они одинаковы. Таким образом, идентификация позволяет только установить принадлежность рассматриваемого сообщения к некоторому классу, без возможности указать какое именно из этих сообщений идентифицируется. Поэтому для идентификации любого сообщения, принадлежащего классу а, потребуется меньше идентифицирующих информации на величину
неразличимы из-за того, что они одинаковы. Таким образом, идентификация позволяет только установить принадлежность рассматриваемого сообщения к некоторому классу, без возможности указать какое именно из этих сообщений идентифицируется. Поэтому для идентификации любого сообщения, принадлежащего классу а, потребуется меньше идентифицирующих информации на величину  , т.е.
, т.е. .
. …,
…, 

 ...,
...,  . (2. 29)
. (2. 29) (2.30)
(2.30) (2.31)
(2.31) (2. 32)
(2. 32) , что совпадает с утверждением теоремы 2.5 и формулой (2.2) для определения количества информации мерой Хартли.
, что совпадает с утверждением теоремы 2.5 и формулой (2.2) для определения количества информации мерой Хартли. (2.33)
(2.33) …,
…,  …,
…,  (2.34)
(2.34) или
или  , (2. 35)
, (2. 35) или
или  . (2. 36)
. (2. 36)


