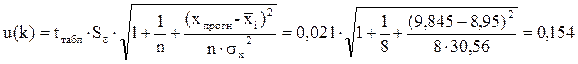Линейная парная регрессия.Наиболее простой с точки зрения понимания, интерпретации и техники расчетов является линейная форма регрессии. Уравнение линейной парной регрессии a0, a1– параметры модели, εi – случайная величина (величина остатка). Параметры модели и их содержание: Ø a0 – свободный коэффициент (член) регрессионного уравнения. Не имеет экономическою смысла и показывает значение результативного признака y, если факторный признак x =0. Ø a1 - коэффициент регрессии показывает, на какую величину в среднем изменится результативный признак y, если переменную х увеличить на единицу измерения. Знак при коэффициенте регрессии показывает направление связи: при a1 > 0 – связь прямая; при a1 < 0 - связь обратная. Ø εi- независимая, нормально распределенная случайная величина, остаток с нулевым математическим ожиданием (Mε=0) и постоянной дисперсией (Dε=σ2). Отражает тот факт, что изменение y будет неточно описываться изменением x, так как присутствуют другие факторы, не учтенные в данной модели. Оценка параметров модели а0 и а, осуществляется методом наименьших квадратов. Сущность метода наименьших квадратов •включается в том, что отыскиваются такие значения параметров модели (a0, a1), при которых сумма квадратов отклонений фактических значений результативного признака
Система нормальных уравнений для нахождения параметра линейной парной регрессии методом наименьших квадратов
Формулы для определения значения параметров a0 и a1
Дисперсия – характеристика случайной величины, определяемая как математическое ожидание квадрата отклонения случайной величины от ее математического ожидания. Математическое ожидание – сумма произведений значений случайной величины на соответствующие вероятности. Параметр a1 нельзя использовать для непосредственной оценки влияния факторного признака на результативный признак из-за различия единиц измерения исследуемых показателей. Для этих целей вычисляют коэффициент эластичности и бета-коэффициент. Формула для определения коэффициента эластичности
Коэффициент эластичности показывает, на сколько процентов изменяется результативный признак у при изменении факторного признака x на один процент. Формулы для определения бета – коэффициента
Бета-коэффициент показывает, на какую часть своего среднего квадратического отклонения изменится в среднем значение результативного признака при изменении факторного признака на величину своего среднего квадратического отклонения. Уравнение регрессии дополняется показателем тесноты связи. В качестве такого показателя выступает линейный коэффициент корреляции
Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции
где
Соответственно величина После того как уравнение регрессии построено, выполняется проверка его адекватности и точности.Эти свойства модели исследуются на основе анализа ряда остатков εi (отклонений расчетных значений от фактических). Уровень ряда остатков Корреляционный и регрессионный анализ проводится для ограниченной по объему совокупности. В связи с этим показатели регрессии, корреляции и детерминации могут быть искажены действием случайных факторов. Чтобы проверить, насколько эти показатели характерны для всей совокупности, не являются ли они результатом стечения случайных обстоятельств, необходимо проверить адекватность построенной модели. Проверка адекватности модели заключается в определении значимости модели и установление наличия или отсутствия систематической ошибки. Значения у1 соответствующие данным х i при теоретических значениях а0 и а1, случайные. Случайными будут и рассчитанные по ним значения коэффициентов а0 и а1. Проверка значимостиотдельных коэффициентов регрессии проводится по t-критерию Стьюдента путем проверки гипотезы равенстве нулю каждого коэффициента регрессии. При этом выясняют, насколько вычисленные параметры характерны для отображения комплекса условий: не являются ли полученные значения параметров результатом действия случайных величин. Для соответствующих коэффициентов регрессии применяют соответствующие формулы. Формулы для определения t- критерия Стьюдента
Sa0,Sa1 - стандартные отклонения свободного члена и коэффициента регрессии. Определяются по формулам
Sε – стандартное отклонение остатков модели (стандартная ошибка оценки), которая определяется по формуле
Расчетные значения t-критерия сравнивают с табличным значением критерия t αγ,.которое определяется при (n — k — 1) степенях свободы и соответствующем уровне значимости α. Если расчетное значение t -критерия превосходит его табличное значение t αγ,то параметр признается значимым. В таком случае практически невероятно, что найденные значения параметров обусловлены только случайными совпадениями. Оценка значимости уравнения регрессии в целом производится на основе Общая сумма квадратов отклонений переменной
, где
Схема дисперсионного анализа имеет вид, представленный в таблице 35 ( Таблица 35 – Схема дисперсионного анализа
Определение дисперсии на одну степень свободы приводит дисперсии к сравнимому виду. Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим величину Для проверки значимости уравнения регрессии в целом используют F-критерий Фишера. В случае парной линейной регрессии значимость модели регрессии определяется по следующей формуле: Если при заданном уровне значимости расчетное значение F -критерия с γ1=k, γ2=(п – k – 1) степенями свободы больше табличного, то модель считается значимой, гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность. Проверка наличия или отсутствия систематической ошибки (выполнения предпосылок метода наименьших квадратов — МНК) осуществляется на основе анализа ряда остатков. Расчет случайных ошибок параметров линейной регрессии и коэффициента корреляции производят по формулам
Для проверки свойства случайности ряда остатков можно использовать критерий поворотных точек (пиков). Точка считается поворотной, если выполняются следующие условия: εi-1 < εi > εi+1 или εi-1 > εi < εi+1 Далее подсчитывается число поворотных точек р. Критерием случайности с 5 % уровнем значимости, т.е. с доверительной вероятностью 95%, является выполнение неравенства: Квадратные скобки означают, что берется целая часть числа, заключенного в скобки. Если неравенство выполняется, то модель считается адекватной. Для проверки равенства математического ожидания остаточной последовательности нулю вычисляется среднее значение ряда остатков:
Если Если
где Sε — стандартное отклонение остатков модели (стандартная ошибка). Значение t -критерий сравнивают с табличным t αγ. Если выполняется неравенство t > t αγ, то модель неадекватна по данному критерию Дисперсия уровней ряда остатков должна быть одинаковой для всех значений х (свойство гомоскедастичности).Если это условие не соблюдается, то имеет место гетероскедастичность. Для оценки гетероскедастичности при малом объеме выборки можно использовать метод Гольдфельда—Квандта, суть которого заключается в том, что необходимо: § расположить значения переменной х в порядке возрастания; § разделить совокупность упорядоченных наблюдений на две группы; § по каждой группе наблюдений построить уравнения регрессии; § определить остаточные суммы квадратов для первой и второй групп по формулам: n1 - число наблюдений в первой группе; n2- число наблюдений во второй группе. § рассчитать критерий
Проверку независимости последовательности остатков (отсутствие автокорреляции)осуществляют с помощью d-критерия Дарбина—Уотсона. Он определяется по формуле:
Расчетное значение критерия сравнивается с нижним d1и верхним d2критическими значениями статистики Дарбина—Уотсона. Возможны следующие случаи: 1) если d < d1, то гипотеза о независимости остатков отвергается и модель признается неадекватной по критерию независимости остатков; 2) если d1 < d < d2(включая сами эти значения), то считается, что нет достаточных оснований сделать тот или иной вывод. Необходимо использовать дополнительный критерий, например первый коэффициент автокорреляции: Если расчетное значение коэффициента по модулю меньше табличного значения г1кр, то гипотеза об отсутствии автокорреляции принимается; в противном случае эта гипотеза отвергается; 3) если d2 < d < 2, то гипотеза о независимости остатков принимается и модель признается адекватной по данному критерию; 4) если d> 2, то это свидетельствует об отрицательной автокорреляции остатков. В этом случае расчетное значение критерия необходимо преобразовать по формуле d′= 4 - dи сравнивать с критическим значением d′, а не d. Проверку соответствия распределения остаточной последовательности нормальному закону распределенияможно осуществить с помощью R/S - критерия, который определяется по формуле: где Sε — стандартное отклонение остатков модели (стандартная ошибка). Расчетное значение R/S - критерия сравнивают с табличными значениями (нижней и верхней границами данного отношения), и если значение не попадает в интервал между критическими границами, то с заданным уровнем значимости гипотеза о нормальности распределения отвергается; в противном случае гипотеза принимается Для оценки качества регрессионных моделей целесообразно также использовать индекс корреляции (коэффициент множественной корреляции). Формула определения индекса корреляции
Уравнение
Индекс корреляции принимает значение от 0 до 1. Чем выше значение индекса, тем ближе расчетные значения результативного признака к фактическим. Индекс корреляции используется при любой форме связи переменных; при парной линейной регрессии он равен парному коэффициенту корреляции. В качестве меры точности модели применяют точностные характеристики: Для определения меры точности модели рассчитывают: Ø максимальная ошибка - соответствует отклонению расчетному отклонению расчетных значений от фактических Ø средняя абсолютная ошибка – ошибка показывает, насколько в среднем отклоняются фактические значения от модели
Ø дисперсия ряда остатков (остаточная дисперсия)
Ø средняя квадратическая ошибка. Представляет собой корень квадратный из дисперсии: Ø средняя относительная ошибка аппроксимации.
Средняя ошибка аппроксимации не должна превышать 8–10%. Если модель регрессии признана адекватной, а параметры модели значимы, то переходят к построению прогноза. Прогнозируемое значение переменной у получается при подстановке в уравнение регрессии ожидаемой величины независимой переменной х прогн.
Данный прогноз называется точечным. Вероятность реализации точечного прогноза практически равна нулю, поэтому рассчитывается доверительный интервал прогноза с большой надежностью. Доверительные интервалы прогноза зависят от стандартной ошибки, удаления х прогн от своего среднего значения
t табл – определяется по таблице распределения Стьюдента для уровня значимости α и числа степеней свободы γ=n-k-1. Пример13. По данным проведенного опроса восьми групп семей известны данные связи расходов населения на продукты питания с уровнем доходов семьи (таблица 36). Таблица 36 – Связи расходов населения на продукты питания с уровнем доходов семьи
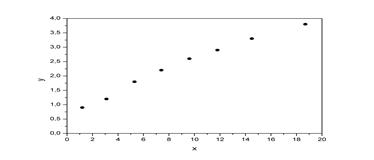
Решение: Предположим, что связь между доходами семьи и расходами на продукты питания линейная. Для подтверждения нашего предположения построим поле корреляции (рисунок 8). По графику видно, что точки выстраиваются в некоторую прямую линию. Для удобства дальнейших вычислений составим таблицу 37. Рассчитаем параметры линейного уравнения парной регрессии
Рисунок 8 – Поле корреляции. Получили уравнение: Т.е. с увеличением дохода семьи на 1000 руб. расходы на питание увеличиваются на 168 руб. Расчет линейного коэффициента корреляции
Близость коэффициента корреляции к 1 указывает на тесную линейную связь между признаками. Таблица 37 – Расчетные показатели.
Расчет коэффициента детерминации Коэффициент детерминации Оценим качество уравнения регрессии в целом с помощью
Табличное значение ( Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитаем
Фактические значения
Табличное значение Рассчитываем среднюю ошибку аппроксимации:
Рассчитываем прогнозное значение результативного фактора
Значит, если доходы семьи составят 9,845 тыс. руб., то расходы на питание будут 2,490 тыс. руб. Рассчитываем доверительный интервал прогноза.
|

 , где
, где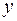 от теоретических
от теоретических  минимальна:
минимальна: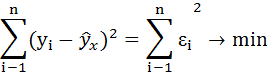


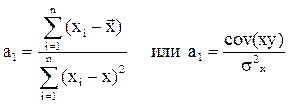 где
где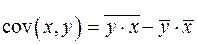 – ковариация признаков
– ковариация признаков 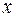 и
и  – дисперсия признака
– дисперсия признака 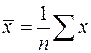 ,
, 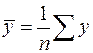 ,
, 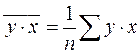 ,
, 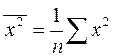 .
.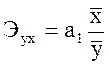
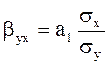 где σx и σy – средние квадратические отклонения случайных величин x и y.
где σx и σy – средние квадратические отклонения случайных величин x и y. , который рассчитывают по формуле:
, который рассчитывают по формуле: или
или  .
.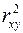 , называемый коэффициентом детерминации. Коэффициент детерминации характеризует долю дисперсии результативного признака
, называемый коэффициентом детерминации. Коэффициент детерминации характеризует долю дисперсии результативного признака 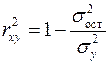 ,
,
 .
. характеризует долю дисперсии
характеризует долю дисперсии 

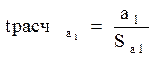 где
где
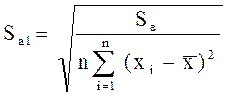 где
где
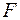 -критерия Фишера, которому предшествует дисперсионный анализ.
-критерия Фишера, которому предшествует дисперсионный анализ.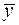 раскладывается на две части – «объясненную» и «необъясненную»:
раскладывается на две части – «объясненную» и «необъясненную»:
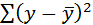 – общая сумма квадратов отклонений;
– общая сумма квадратов отклонений; – сумма квадратов отклонений, объясненная регрессией (или факторная сумма квадратов отклонений);
– сумма квадратов отклонений, объясненная регрессией (или факторная сумма квадратов отклонений);
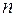 – число наблюдений,
– число наблюдений,  – число параметров при переменной
– число параметров при переменной 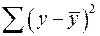

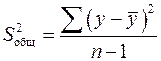
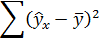
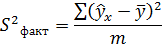

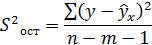
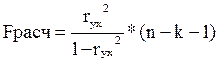 .
.
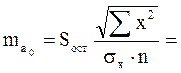 ,
,
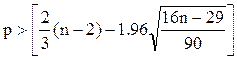

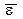 = 0, то считается, что модель не содержит постоянной систематической ошибки и адекватна по критерию нулевого среднего.
= 0, то считается, что модель не содержит постоянной систематической ошибки и адекватна по критерию нулевого среднего.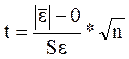
 ;
;  , где
, где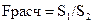 или
или 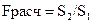 (в числителе должна быть большая сумма квадратов). При выполнении нулевой гипотезы о гомоскедастичности критерий Fрасч будет удовлетворять F-критерию со степенями свободы γ1=n1-m, γ2=n – n1 – m) для каждой остаточной суммы квадратов (где m — число оцениваемых параметров в уравнении регрессии). Чем больше величина Fрасчпревышает табличное значение F- критерия, тем больше нарушена предпосылка о равенстве дисперсий остаточных величин.
(в числителе должна быть большая сумма квадратов). При выполнении нулевой гипотезы о гомоскедастичности критерий Fрасч будет удовлетворять F-критерию со степенями свободы γ1=n1-m, γ2=n – n1 – m) для каждой остаточной суммы квадратов (где m — число оцениваемых параметров в уравнении регрессии). Чем больше величина Fрасчпревышает табличное значение F- критерия, тем больше нарушена предпосылка о равенстве дисперсий остаточных величин.
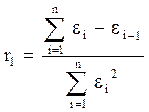
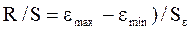
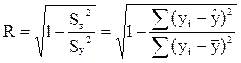 где
где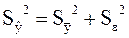
 – общая сумма квадратов отклонений зависимой переменной от ее среднего значения. Определяется по формуле:
– общая сумма квадратов отклонений зависимой переменной от ее среднего значения. Определяется по формуле: 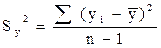
 - сумма квадратов отклонений, объясненная регрессией. Определяется по формуле:
- сумма квадратов отклонений, объясненная регрессией. Определяется по формуле: 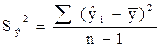
 - остаточная сумма квадратов отклонений. Вычисляется по формуле:
- остаточная сумма квадратов отклонений. Вычисляется по формуле: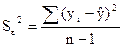
 можно представить следующим образом:
можно представить следующим образом: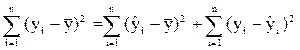

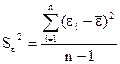 где
где  - среднее значение ряда остатков. Определяется по формуле
- среднее значение ряда остатков. Определяется по формуле 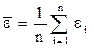
 , чем меньше значение ошибки, тем точнее модель
, чем меньше значение ошибки, тем точнее модель

 , количества наблюдений n и уровня значимости прогноза α. Доверительные интервалы прогноза рассчитывают по формуле:
, количества наблюдений n и уровня значимости прогноза α. Доверительные интервалы прогноза рассчитывают по формуле:  или
или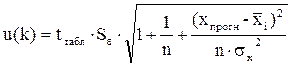 где
где . Для этого воспользуемся формулами:
. Для этого воспользуемся формулами:
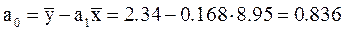

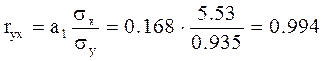









 показывает, что уравнением регрессии объясняется 98,7% дисперсии результативного признака, а на долю прочих факторов приходится лишь 1,3%.
показывает, что уравнением регрессии объясняется 98,7% дисперсии результативного признака, а на долю прочих факторов приходится лишь 1,3%.
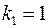 ,
,  ,
,  ):
): 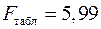 . Т. к.
. Т. к.  , то признается статистическая значимость уравнения в целом.
, то признается статистическая значимость уравнения в целом. -критерий Стьюдента и доверительные интервалы каждого из показателей. Рассчитаем случайные ошибки параметров линейной регрессии и коэффициента корреляции
-критерий Стьюдента и доверительные интервалы каждого из показателей. Рассчитаем случайные ошибки параметров линейной регрессии и коэффициента корреляции
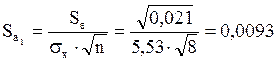
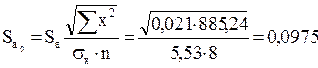
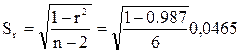


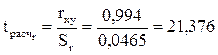
 есть
есть  . Так как
. Так как  , то признаем статистическую значимость параметров регрессии и показателя тесноты связи.
, то признаем статистическую значимость параметров регрессии и показателя тесноты связи.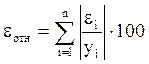 , вычисления заносим в таблицу ст.10
, вычисления заносим в таблицу ст.10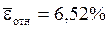 говорит о хорошем качестве уравнения регрессии, т.е. свидетельствует о хорошем подборе модели к исходным данным.
говорит о хорошем качестве уравнения регрессии, т.е. свидетельствует о хорошем подборе модели к исходным данным. при значении признака-фактора, составляющем 110% от среднего уровня
при значении признака-фактора, составляющем 110% от среднего уровня , т.е. найдем расходы на питание, если доходы семьи составят 9,85 тыс. руб.
, т.е. найдем расходы на питание, если доходы семьи составят 9,85 тыс. руб.