Системы линейных алгебраических уравненийОбщий вид системы линейных алгебраических уравнений следующий:
где а ij, i=1,...m; j=1,…n—неизвестные величины, называемые коэффициентами системы уравнений. Первый индекс означает номер уравнения, второй—номер неизвестного, при котором стоит коэффициент; bi, i=1,…m—известные величины, называемые свободными членами, или правыми частями уравнений; xj, j=1,…n—неизвестные переменные величины (или просто неизвестные). Система (2)— система линейных уравнений, т.к. все неизвестные входят во все уравнения только в первой степени. Матрица А, составленная из коэффициентов системы, называется матрицей системы. Матрица системы, дополненная столбцом свободных членов А= Систему (2) можно записать в матричном виде АХ=В, где Х= Набор чисел Решить систему значит найти все её решения или доказать, что не существует ни одного её решения. Если решений бесконечное множество, то указать способ нахождения каждого из них. Система линейных уравнений называется совместной, если она имеет хотя бы одно решение. Система, не имеющая ни одного решения, называется несовместной. Если совместная система имеет единственное решение, то она называется определённой, а если более одного решения, то неопределенной. Две системы алгебраических линейных уравнений называют эквивалентными или равносильными, если они имеют одно и то же множество решений.
|

 (2),
(2), А│В, называется расширенной матрицей системы:
А│В, называется расширенной матрицей системы: , А│В=
, А│В= 
 ; В=
; В=  (3).
(3).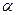 1,
1,  2,…,
2,…, 


