Замена переменных в двойном интегралеЗамена переменных в двойном интеграле часто существенно упрощает его вычисление. I. Пусть D – связный простой компакт, расположенный в плоскости OXY, а функция f(x;y) непрерывна на этом компакте. Пусть, далее, компакт D*, расположенный в плоскости O'UV и отображение F, определяемое парой функций
0 x x 0' u u Рис.1 таковы, что 1) Отображение F компакта D* на D взаимно однозначно; 2) Функции (1) непрерывно – дифференцируемы в D* 3) Якобиан отображение (2) отличен от нуля в D*:
Последнее равенство запишем короче в виде
Такое отображение будем называть регулярным. При регулярном отображении (1) внутренние точки P*(u;v) компакта D * переходят во внутренние точки P (u;v) компакта D, а при обратном отображении F-1
внутренние точки P (x;y) компакта переходят D во внутренние точки P*(u;v) компакта D*. Кроме того
Возьмем в D * прямую
(параметром здесь является v). Аналогично, каждая прямая
компакта D. Линии (4) и(5) называются координатными линиями (на компакте плоскости OXY). Эти линии, вообще говоря, кривые (см.Рис.2).
0’ u0 u 0 x Рис.2 Таким образом, в силу взаимной однозначности отображения (1) через каждую точку (x;y) компакта D проходит единственная линия вида (4) при постоянном значении u и единственная линия вида (5) при постоянном значении v. Эти величины u и v называют криволинейными координатами точки (x;y). Перейдем теперь к преобразованию двойного интеграла
от непрерывной на связном простом компакте D функции f(x;y) с помощью рассмотренного выше регулярного отображения F. Имеем
где s – интегральная сумма для функции f(x;y), соответствующая произвольному разбиению T компакта D на любое конечное число квадрируемых ячеек, при произвольном выборе точек (x;h) в этих ячейках, l(T) - наибольший из диаметров этих ячеек. Возьмем в качестве T разбиения компакта D на криволинейные ячейки, соответствующие разбиениюкомпакта D * на ячейки с помощью прямых, параллельных осям O’U, O’V.
Рис.3 Поскольку площадь границы компакта D равна нулю, то двойной интеграл можно рассматривать как предел суммы только тех слагаемых интегральной суммы s, которые соответствуют внутренним ячейкам разбиения T компакта D. Поэтому
где
Переходя к декартовым координатам вершин этого четырехугольника будем иметь:
где
Введем обозначения
Считая, в целях сокращения выкладок, что функции
Так как остаточные члены
Таким образом, можно считать:
Легко проверить, что
так, что прямолинейная фигура
*) При вычислении предела (7), как показано в [4], можно обойтись и без этого предположения.
равна удвоенной площади треугольника
Имеем
т.е.
Следовательно,
- интегральная сумма для непрерывной в D * функции Предел этой суммы при
Теперь (7) можно переписать в виде
Таким образом, имеет место следующая теорема. Теорема (о замене переменных в двойном интеграла). Если отображение (1) компакта D* на D регулярно, то справедлива формула (8). Пример. Вычислим à Введем новые переменные
Тогда По формулам (9) квадрат преобразуется в квадрат
0 1 3 x Рис.4
Так как
то согласно (8) имеем
Поскольку
¨
|


 (1)
(1)

 y v
y v



 P v
P v

 y DD D D*
y DD D D* C C*
C C*

 . (2)
. (2) .
. (3)
(3) .
.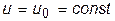 . При отображении (1) ей в D отвечает линия, определяемая параметрическими уравнениями
. При отображении (1) ей в D отвечает линия, определяемая параметрическими уравнениями (4)
(4) компакта D * отображается на линию
компакта D * отображается на линию (5)
(5)




















 v y
v y


 v0 u0
v0 u0  v0
v0

 , (6)
, (6)













 v y
v y



 vi+1
vi+1
 vi
vi  0’ uk u k+1 u 0 x
0’ uk u k+1 u 0 x

 , (7)
, (7) – площадь криволинейного четырехугольника
– площадь криволинейного четырехугольника  , ограниченного линиями
, ограниченного линиями .
. ,
,
 .
. и
и  имеют в D * непрерывные частные производные второго порядка *) и пользуясь формулой Тейлора для функции 2-х переменных, получим:
имеют в D * непрерывные частные производные второго порядка *) и пользуясь формулой Тейлора для функции 2-х переменных, получим: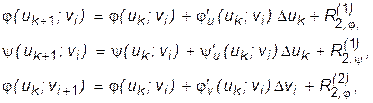

 являются бесконечно малыми величинами высшего порядка малости по сравнению с
являются бесконечно малыми величинами высшего порядка малости по сравнению с  и
и  при
при  , то они не влияют на величину предела интегральной суммы, поэтому при нахождении этого предела их можно отбросить.
, то они не влияют на величину предела интегральной суммы, поэтому при нахождении этого предела их можно отбросить.

 является параллелограммом, площадь которого
является параллелограммом, площадь которого
 , т.е. модулю определителя (см., например, [6], стр.72)
, т.е. модулю определителя (см., например, [6], стр.72) .
.
 .
. -
- .
. существует и равен двойному интегралу
существует и равен двойному интегралу .
.
 , если область D - квадрат, ограниченный прямыми
, если область D - квадрат, ограниченный прямыми  .
. . (9)
. (9) .
. (см.Рис. 4).
(см.Рис. 4).



 1
1



 3 1 3
3 1 3 -1 u
-1 u ,
, .
. , то
, то .
.


