Основные теоремы дифференциального исчисления
Теорема Ролля. Пусть функция у= f(х) удовлетворяет следующим условиям: 1) непрерывная на отрезке 2) дифференцируема в интервале 3) на концах отрезка принимает равные значения, то есть Тогда в середине отрезка существует хотя бы одна такая точка С геометрической точки зрения это означает, что если функция у= f(х) удовлетворяет условиям теоремы Ролля, то в середине отрезка обнаружится хотя бы одна точка, в которой касательная к графику функции будет параллельна оси абсцисс. На рис. 5.6 таких точек две:
Если Все требования теоремы Ролля являются существенными и при невыполнении хотя бы одной из них вывод теоремы может быть неверным, что легко увидеть с помощью геометрической иллюстрации.
Рис. 5.7 На рис. 5.7, а – нарушено условие непрерывности на отрезке на рис. 5.7, бы - нарушено условие дифференцируемости на интервале на рис. 5.7, в - нарушено условие В результате ни в одном случае не существует такой точки Теорема Ролля есть частным случаем теоремы Лагранжа. ТеоремаЛагранжа (о конечном приращении функции). Пусть функция у= f(х) удовлетворяет следующим условиям: 1) непрерывна на отрезке 2) дифференцируема на интервале Тогда в середине отрезка существует хотя бы одна такая точка
Введем новую функцию
Функция
Значит, существует точка Формула (5.25) может быть переписана в виде Выясним содержание теоремы Лагранжа. Приращение Геометрическое содержание вытекает из рис. 5.8.
Если передвигать прямую АВ параллельно начальному положению, то обнаружится хотя бы одна точка а касательной Следствие. Если производная функции Рассмотренные теоремы используются для доказательства многих теоретических положений, результаты которых уже непосредственно используются для решения практических задач. Следующая теорема имеет именно такой характер, она дает практическое правило для раскрытия неопределенностей вида Теорема 5.8 (правило Лопиталя). Пусть
Если отношение Пример 5.1. Вычислить предел Решение. Имеем неопределенность типа
Пример 5.2. Вычислить Решение. Имеем неопределенность типа
5. Применение производной к исследованию функции и построения ее графика
|

 ;
; ;
; .
. , в которой производная функции равна нулю:
, в которой производная функции равна нулю:  .
. и
и  .
.
 , это теорема Ролля утверждает, что между двумя последовательными нулями дифференцируема функции есть хотя бы один нуль производной.
, это теорема Ролля утверждает, что между двумя последовательными нулями дифференцируема функции есть хотя бы один нуль производной.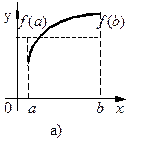


 , в которой
, в которой  , в которой производная равна частному от деления приращения функции на приращение аргумента на этом отрезке, то есть
, в которой производная равна частному от деления приращения функции на приращение аргумента на этом отрезке, то есть (5.25)
(5.25) следующим образом:
следующим образом:


 , или
, или  , ведь
, ведь  откуда
откуда  .
.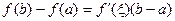 . (5.26)
. (5.26) - это изменение функции на
- это изменение функции на  - это средняя скорость изменения функции на этом отрезке; значения производной в точке - это мгновенная скорость изменения функции. Таким образом, теорема утверждает: существует хотя бы одна точка в середине отрезка такая, что скорость изменения функции в ней равна средней скорости изменения функции на этом отрезке.
- это средняя скорость изменения функции на этом отрезке; значения производной в точке - это мгновенная скорость изменения функции. Таким образом, теорема утверждает: существует хотя бы одна точка в середине отрезка такая, что скорость изменения функции в ней равна средней скорости изменения функции на этом отрезке.
 и хорда АВ, проведенная через концы дуги АВ, параллельны. (Так как угловой коэффициент секущей АВ
и хорда АВ, проведенная через концы дуги АВ, параллельны. (Так как угловой коэффициент секущей АВ  ,
, ).
). или
или  . Сформулируем ее.
. Сформулируем ее.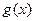 - непрерывны и имеют производные во всех точках
- непрерывны и имеют производные во всех точках 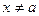 из окрестности точки
из окрестности точки 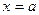 , а в точке
, а в точке  равны нулю или бесконечности. Тогда предел отношения функций равен пределу отношения их производных, если последняя существует, то есть
равны нулю или бесконечности. Тогда предел отношения функций равен пределу отношения их производных, если последняя существует, то есть . (5.27)
. (5.27) снова является неопределенностью вида
снова является неопределенностью вида  и
и  удовлетворяют условиям правила Лопиталя, то для вычисления предела можно применить правило Лопиталя вторично и так далее.
удовлетворяют условиям правила Лопиталя, то для вычисления предела можно применить правило Лопиталя вторично и так далее.


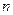 раз, получим
раз, получим



