Прежде чем дать общее определение предела функции, рассмотрим примеры.
Пример 1. Пусть  . Рассмотрим таблицу значений этой функции вблизи точки x = 3.
. Рассмотрим таблицу значений этой функции вблизи точки x = 3.
| x
| 2,94
| 2,96
|
| 3,02
| 3,04
| 3,06
|

|
5,94
|
5,96
| функция не
определена
|
6,02
|
6,04
|
6,06
|
При x = 3функция не определена. Если же значения xвыбрать достаточно близкими к трём, то значения f (x)оказываются, как видно из таблицы, достаточно близкими к 6. Докажем это строго математически, а именно: покажем, что для любого  , как бы мало оно ни было, можно указать такую окрестность точки x = 3, что всюду внутри неё, за исключением самой точки, будет выполняться неравенство
, как бы мало оно ни было, можно указать такую окрестность точки x = 3, что всюду внутри неё, за исключением самой точки, будет выполняться неравенство  .
.
Действительно, если  , то
, то  , поэтому
, поэтому  при
при  . Таким образом, неравенство
. Таким образом, неравенство  выполняется при всех
выполняется при всех 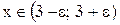 , кроме
, кроме  .
.
 y Если, например, мы хотим, чтобы зна-
y Если, например, мы хотим, чтобы зна-
 чения f(x) отличались от 6 менее чем на
чения f(x) отличались от 6 менее чем на
6+e  , то должны рассматривать
, то должны рассматривать

 . Аналогично при
. Аналогично при 
6-e получим интервал (2,999; 3,001) и т.д.
Интервал  можно построить
можно построить
геометрически (рис. 1).
Итак, если значения аргумента x
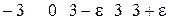 x выбрать достаточно близкими к 3, но
x выбрать достаточно близкими к 3, но
Рис. 1 не равными 3, то значения функции будут сколь угодно мало отличаться от 6. Несмотря на то что рассматриваемая функция не определена при  , естественно считать, что её предел при
, естественно считать, что её предел при  (x cтремящемся к 3) существует и равен 6:
(x cтремящемся к 3) существует и равен 6:
 .
.
Рассмотрим ещё один пример.
Пример 2. Пусть  . Не рассуждая столь подробно, как в примере 1, отметим очевидный факт: чем ближе значения аргумента xк 2, тем ближе значения
. Не рассуждая столь подробно, как в примере 1, отметим очевидный факт: чем ближе значения аргумента xк 2, тем ближе значения  к 4, то есть, тем меньше абсолютная величина разности
к 4, то есть, тем меньше абсолютная величина разности  . Действительно, какое бы малое число y
. Действительно, какое бы малое число y

 мы ни взяли, всегда можно
мы ни взяли, всегда можно 
указать такой интервал, содержащий 
точку  , что для всех для точек из этого интервала будет выполняться 4
, что для всех для точек из этого интервала будет выполняться 4
неравенство  . На рис. 2
. На рис. 2
 при всех
при всех 
 . Так как
. Так как  ,
,
то полагая  , можем
, можем  x
x
утверждать, что если 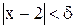 ,
,
то  . Рис. 2
. Рис. 2
Таким образом, так же, как и в
примере 1, если значения x выбрать достаточно близкими к 2, то значения функции 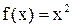 будут как угодно мало отличаться от 4, и число 4естественно назвать пределом функции при x, стремящемся к 2:
будут как угодно мало отличаться от 4, и число 4естественно назвать пределом функции при x, стремящемся к 2:
 .
.
Перейдём к определению предела функции в точке.
Определение 1. Число b называется пределом функции  при
при  , если для любого положительного
, если для любого положительного  можно указать такой интервал, содержащий точку
можно указать такой интервал, содержащий точку  , что всюду внутри него, за исключением, быть может, самой точки
, что всюду внутри него, за исключением, быть может, самой точки  , будет выполняться неравенство
, будет выполняться неравенство  .
.
Другими словами,  , если для любого
, если для любого  найдётся зависящее от
найдётся зависящее от  такое, что для всех x, удовлетворяющих неравенству
такое, что для всех x, удовлетворяющих неравенству  , справедливо следующее:
, справедливо следующее:  .
.
Пример 3. Рассмотрим функцию  , которая определена при всех
, которая определена при всех  . Составим таблицу её значений и построим график.
. Составим таблицу её значений и построим график.
| x
|
|
|
|
|
|
| ...
| -1
| -2
| -3
| -4
| -10
| -100
|
| x-1
x
|
| 1
| 2
| 3
| 9
| 99
|
...
|
| 3
| 4
| 5
| 11
| 101
|
Исследуя таблицу и график (рис. 3), можно предположить, что с
возрастанием  значения
значения  неограниченно приближаются к 1.
неограниченно приближаются к 1.
Чтобы доказать это, вычислим  - расстояние от точки А
- расстояние от точки А  на графике функции до прямой
на графике функции до прямой  :
:  .
.
Очевидно, если значение  достаточно велико, найденное расстояние может быть меньше любого наперёд заданного числа. Действительно,
достаточно велико, найденное расстояние может быть меньше любого наперёд заданного числа. Действительно,  при
при  ,
,  при
при  и т.д.
и т.д.
Вообще, для произвольно заданного 
 , если
, если  (при всех
(при всех  или
или  ).
).
y


1

x
 x
x
Рис. 3
Дадим определение предела функции на бесконечности.
Определение 2. Число b называется пределом функции  при
при  (
( ), если для любого положительного числа
), если для любого положительного числа  найдётся отвечающее ему положительное число Атакое, что для всех
найдётся отвечающее ему положительное число Атакое, что для всех  (или
(или  ) справедливо неравенство
) справедливо неравенство  .
.
В рассмотренном примере 3  и
и  . Кроме того, ясно, что
. Кроме того, ясно, что  .
.
Заметим, что не для всякой функции  существует
существует  или
или  . Например, при
. Например, при  значения функции
значения функции  (рис. 4)
(рис. 4)
 или неограниченно растут при (
или неограниченно растут при ( ), или неограниченно убывают (при
), или неограниченно убывают (при  ).
).
Поэтому нельзя указать никакого числаb, y
к которому стремились бы значения 
этой функции при  .
.
Другой пример. Рассмотрим функцию, 0  x
x
определённую следующим образом:
 Рис. 4
Рис. 4
 График этой функции дан на рис. 5. y
График этой функции дан на рис. 5. y
Когда значения аргумента x стремятся к 0,
оcтаваясь отрицательными, соответствую- 1
щие значения функции  приближа-
приближа-
ются к (-1). Когда же значения аргумен- -1 0 1 x
та xприближаются к 0, оставаясь поло-
жительными, соответствующие значения -1
функции  стремятся к 1. При этом
стремятся к 1. При этом
 . Очевидно, что указать какое- Рис. 5
. Очевидно, что указать какое- Рис. 5
либо число, к которому стремились бы
все значения  при
при  , нельзя. Поэтому для данной функции
, нельзя. Поэтому для данной функции  не существует. Хотя предел этой функции в любой другой точке вычислить можно: к примеру
не существует. Хотя предел этой функции в любой другой точке вычислить можно: к примеру  или
или  .
.
Точно так же нельзя указать такое число b, к которому бы стремились все значения функции  (рис. 6) при неограниченном возрастании
(рис. 6) при неограниченном возрастании  (при
(при  ), так как величина
), так как величина  совершает гармонические колебания с постоянной амплитудой, всё время
совершает гармонические колебания с постоянной амплитудой, всё время 


 изменяясь от (-1) до (+1). Поэтому
изменяясь от (-1) до (+1). Поэтому  не существует.
не существует.
 y
y
-  0
0  x
x
Рис. 6
Пример 4. Исходя из определения предела, доказать, что  .
.
Зададим произвольное  и найдём, при каких значениях xвыполняется
и найдём, при каких значениях xвыполняется
неравенство  .
.
 при всех
при всех  . Таким образом, если
. Таким образом, если
 или
или  , то
, то  , а это означает по определению 1, что
, а это означает по определению 1, что  .
.
Пример 5. Исходя из определения предела, доказать, что  .
.
Зададим произвольное  .
.  . Отсюда следует, что если
. Отсюда следует, что если  или
или  , то
, то  . Таким образом, действительно,
. Таким образом, действительно,  по определению 2.
по определению 2.

 . Рассмотрим таблицу значений этой функции вблизи точки x = 3.
. Рассмотрим таблицу значений этой функции вблизи точки x = 3.
 , как бы мало оно ни было, можно указать такую окрестность точки x = 3, что всюду внутри неё, за исключением самой точки, будет выполняться неравенство
, как бы мало оно ни было, можно указать такую окрестность точки x = 3, что всюду внутри неё, за исключением самой точки, будет выполняться неравенство  .
. , то
, то  , поэтому
, поэтому  при
при  . Таким образом, неравенство
. Таким образом, неравенство 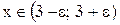 , кроме
, кроме  .
. y Если, например, мы хотим, чтобы зна-
y Если, например, мы хотим, чтобы зна- , то должны рассматривать
, то должны рассматривать
 . Аналогично при
. Аналогично при 
 можно построить
можно построить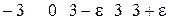 x выбрать достаточно близкими к 3, но
x выбрать достаточно близкими к 3, но (x cтремящемся к 3) существует и равен 6:
(x cтремящемся к 3) существует и равен 6: .
. . Не рассуждая столь подробно, как в примере 1, отметим очевидный факт: чем ближе значения аргумента xк 2, тем ближе значения
. Не рассуждая столь подробно, как в примере 1, отметим очевидный факт: чем ближе значения аргумента xк 2, тем ближе значения  к 4, то есть, тем меньше абсолютная величина разности
к 4, то есть, тем меньше абсолютная величина разности  . Действительно, какое бы малое число y
. Действительно, какое бы малое число y
 мы ни взяли, всегда можно
мы ни взяли, всегда можно 

 , что для всех для точек из этого интервала будет выполняться 4
, что для всех для точек из этого интервала будет выполняться 4 . На рис. 2
. На рис. 2 при всех
при всех 
 . Так как
. Так как  ,
, , можем
, можем  x
x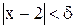 ,
, . Рис. 2
. Рис. 2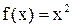 будут как угодно мало отличаться от 4, и число 4естественно назвать пределом функции при x, стремящемся к 2:
будут как угодно мало отличаться от 4, и число 4естественно назвать пределом функции при x, стремящемся к 2: .
. , если для любого положительного
, если для любого положительного  можно указать такой интервал, содержащий точку
можно указать такой интервал, содержащий точку  , что всюду внутри него, за исключением, быть может, самой точки
, что всюду внутри него, за исключением, быть может, самой точки  .
. , если для любого
, если для любого  такое, что для всех x, удовлетворяющих неравенству
такое, что для всех x, удовлетворяющих неравенству  , справедливо следующее:
, справедливо следующее:  , которая определена при всех
, которая определена при всех  . Составим таблицу её значений и построим график.
. Составим таблицу её значений и построим график. значения
значения  - расстояние от точки А
- расстояние от точки А  на графике функции до прямой
на графике функции до прямой  :
:  .
. достаточно велико, найденное расстояние может быть меньше любого наперёд заданного числа. Действительно,
достаточно велико, найденное расстояние может быть меньше любого наперёд заданного числа. Действительно,  при
при  ,
,  при
при  и т.д.
и т.д. , если
, если  (при всех
(при всех  или
или  ).
).


 x
x (
( ), если для любого положительного числа
), если для любого положительного числа  (или
(или  ) справедливо неравенство
) справедливо неравенство  и
и  . Кроме того, ясно, что
. Кроме того, ясно, что  .
. существует
существует  или
или  . Например, при
. Например, при  значения функции
значения функции  (рис. 4)
(рис. 4) или неограниченно растут при (
или неограниченно растут при ( ), или неограниченно убывают (при
), или неограниченно убывают (при  ).
). x
x Рис. 4
Рис. 4 График этой функции дан на рис. 5. y
График этой функции дан на рис. 5. y . Очевидно, что указать какое- Рис. 5
. Очевидно, что указать какое- Рис. 5 , нельзя. Поэтому для данной функции
, нельзя. Поэтому для данной функции  не существует. Хотя предел этой функции в любой другой точке вычислить можно: к примеру
не существует. Хотя предел этой функции в любой другой точке вычислить можно: к примеру  или
или  .
. (рис. 6) при неограниченном возрастании
(рис. 6) при неограниченном возрастании  (при
(при  ), так как величина
), так как величина 


 не существует.
не существует. y
y 0
0  .
. .
. при всех
при всех  . Таким образом, если
. Таким образом, если или
или  , то
, то  , а это означает по определению 1, что
, а это означает по определению 1, что  .
. .
. . Отсюда следует, что если
. Отсюда следует, что если  или
или  , то
, то  . Таким образом, действительно,
. Таким образом, действительно,  по определению 2.
по определению 2.


