ЛАБОРАТОРНАЯ РАБОТА № 10.Производные высших порядков, ряд Тейлора. Если функция f:ХàR,xÎR,дифференцируема в "xÎX,то на множестве X возникает функция f ¢:XàR,значение которой в точке xÎX равно производной f ¢ (x).Если же функция f ¢:XàR имеет производную (f ¢)¢:XàR на множестве x,то (f ¢)¢(x) называется второй производной функции f(x) и обозначается f ²(x) или
Производная n -го порядка является производной от производной (n -1) порядка, т.е. f(n)=(f(n-1))/ (x) Производные, начиная со второй, называются производными высших порядков и обозначаются у//,у///,у(4),…у(n), Производные n-го порядка некоторых элементарных функций: 1. ( 2. (sinx)(n)= 3. (xm)(n)=m(m-1)…(m-n+1)xm-n 4. (ex)(n)=ex 5. (cosx)(n)= 6. (lnx)(n)= Если функции u=j(x) и v=y(x) имеют производные n-го порядка (n- кратно дифференцируемы),
Пример 1: Вычислить n -ю производную (n ³2) функции y=x2cosx. Решение: полагая u=cosx и v=x2, найдем u(n)=cos(x+nп/2), v'=2x, v''=2,v''''=v(4)=…=0. Подставляя в формулу (1), получаем y(n)=c0ncos(x+nп/2)x2+c1ncos(x+(n-1)п/2)2x+c2ncos(x+(n-2)п/2)2 Формула (1) называется формулой Лейбница. Опр. Функция у называется заданной параметрически, если зависимость между у и х задана системой уравнений
Производные этой функции могут быть найдены по формулам:
Пример 2. Найти производные Решение:
Формула Тейлора. Пусть функция f(x) имеет в точке а и некоторой ее окрестности производные порядка n+1. Пусть х-любое значение аргумента из указанной окрестности, х= а. Тогда между точками а и х найдется точка x такая, что справедлива следующая формула:
Пример 3. Разложить в ряд Тейлора функции у=1/х при а =-2. Решение: вычисляем значения данной функции и ее производных при х= а =-2
Подставляя эти значения в формулу Тейлора для произвольной функции, получим
ВАРИАНТЫ. 1. Найти
2. Доказать, что функция у удовлетворяет соотношению: 3. Используя формулу Лейбница, найти:
4. Используя формулу Тейлора, разложить функцию y= f (x) по степеням (х-х
|

 . Если f ²(x) имеет производную (f ²(x))¢,то эта производная называется третьей производной функции f(x) или производной третьего порядка функции f(x) и обозначаются одним из символов f ²¢(x),f(3)(x),
. Если f ²(x) имеет производную (f ²(x))¢,то эта производная называется третьей производной функции f(x) или производной третьего порядка функции f(x) и обозначаются одним из символов f ²¢(x),f(3)(x),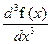

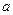 x)(n)=
x)(n)= 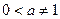 )
)


 (1)
(1)
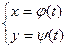 ,tÎT
,tÎT
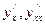 от функции y=y(x), заданной параметрически если x=acost, y=asint
от функции y=y(x), заданной параметрически если x=acost, y=asint
 Частный, простейший вид формулы Тейлора при а =0 принято называть формулой Маклорена:
Частный, простейший вид формулы Тейлора при а =0 принято называть формулой Маклорена: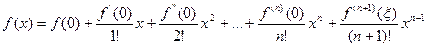
















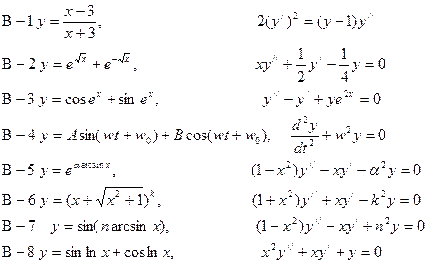








 );
);






