Упражнения к § 2Доказать, что все n-мерные векторы, у которых первая и последняя координаты равны между собой, образуют линейное подпространство. Найти его базис и размерность.
Доказать, что все n-мерные векторы, у которых координаты с четными номерами равны между собой, образуют линейное подпространство. Найти его базис и размерность.
Доказать, что все симметрические матрицы образуют линейное подпространство пространства всех квадратных матриц порядка n. Найти его размерность и базис.
Доказать, что линейное пространство
Доказать, что пространство всех квадратных матриц есть прямая сумма пространств симметрических матриц и кососимметрических матриц.
Доказать, что решения любой системы однородных линейных уравнений с n неизвестными ранга r образуют линейное подпространство n- мерного пространства
§ 3. Определители и линейная независимость векторов
Пусть X – конечномерное линейное пространство и Определение 1. Векторы Число базисных векторов называется рангом системы векторов Для того чтобы векторы Столбцы матрицы A, на которых расположен базисный минор матрицы A, являются базисными векторами для системы векторов Задача 1. Найти базисные векторы в системе векторов Решение. Составим матрицу из координат векторов Найдем какой-либо базисный минор матрицы A. Рассмотрим Следовательно, rang(A)=3. Так как базисный минор расположен на векторах
Упражнения к § 3
1. Найти размерность и базис линейных подпространств, натянутых на следующие системы векторов: 2)
3)
§ 4. Линейные нормированные пространства Определение 1. Линейное пространство над полем K (K =R или K =C) называется нормированным, если задана функция 1) 2) 3) для любых векторов Величина Задача 1. Доказать, что линейное пространство 1. 2. 3. где Решение. Докажем, что для Так как
Таким образом, II. Докажем, что Так как
Таким образом, Аналогично проверяется (доказательство проведите самостоятельно), что
Задача 2. Докажите неравенство Решение. 1) 2) Из пунктов 1) и 2) следует, что
§ 5. Пространства со скалярным произведением. Евклидовы пространства
Определение 1. В n-мерном линейном пространстве H над полем K определена операция скалярного умножения векторов, если задана функция I. II. III. IV. При K=R условие 4) выглядит следующим образом: Конечномерное линейное пространство со скалярным произведением называется евклидовым пространством. Каждое пространство H со скалярным произведением можно сделать нормированным, если положить Задача 1. Доказать, что отображение Решение. Проверим выполнение аксиом скалярного произведения. 1. 2. 3. 4. Таким образом,
Задача 2. Проверить, задает ли отображение Решение. Проверим свойства скалярного произведения. Рассмотрим Рассмотрим Задача 3. Пусть
задает скалярное произведение. Верно ли это утверждение для Решение. Рассмотрим числа
Пусть
Таким образом, при Пусть
Определение 2. Углом между векторами
Задача 4. Определить угол между векторами Решение. В пространстве Тогда
Задача 5. Вычислить угол Решение.
Определение 3. Два вектора Определение 4. Система векторов называется ортогональной, если в ней все векторы попарно ортогональны. Определение 5. Система векторов
Определение 6. Базис Переход от линейно независимых векторов к ортонормированному множеству осуществляется с помощью процесса ортогонализации Грама-Шмидта. Процесс ортогонализации Грама-Шмидта. Пусть
образуют ортонормированное множество в H. В частности, Задача 6. Применить процесс ортогонализации к системе векторов пространства Решение. Применим к линейно независимым векторам
Ортонормированная система векторов: Задача 7. Проверить, что векторы Решение. Проверим, что множество
Векторы
Размерность пространства решений системы равна 1, фундаментальную систему решений и базис в пространстве решений образует вектор Пронормируем f, положив Векторы Задача 8. Найдите какой-нибудь ортонормированный базис в пространстве Решение. Найдем произвольный базис в пространстве M. Размерность пространства M равна 2 (dim M=2) и легко проверить, что векторы
образуют базис, ортогональны и
Векторы
Задача 9. Построить ортонормированный базис подпространства, натянутого на систему векторов Решение. Найдем базис в линейной оболочке векторов Векторы Применим к базисным векторам процесс ортогонализации Грама-Шмидта:
Векторы Определение 7. Пусть M – подпространство из H. Вектор x называется перпендикулярным (ортогональным) подпространству M, если Ортогональным дополнением подпространства M пространства H называется совокупность Для подпространства M евклидова пространства H ортогональное дополнение
Задача 10. Найдите ортонормированный базис в ортогональном дополнении к подпространству M евклидова пространства Решение. Векторы Найдем какой-либо базис в
т.е. a,b – базис в пространстве решений системы однородных уравнений:
Фундаментальной системой решений и базисом в Векторы a,b являются ортогональными, так как
Векторы
Задача 11. Найти ортонормированный базис ортогонального дополнения
Решение. Найдем базис в подпространстве M. Составим матрицу Ранг матрицы A равен 2, базис образуют векторы Так как dim
Общим решением системы является:
Фундаментальная система решений:
Векторы
Векторы Определение 8. Пусть M – подпространство из H. Вектор a называется ортогональной проекцией вектора Теорема. Пусть M – конечномерное подпространство из H и
является единственной ортогональной проекцией вектора x на M.
Задача 12. Найти ортогональную проекцию вектора Решение. Найдем ортонормированный базис в пространстве
Найдем проекцию
Таким образом,
Укажем другой способ решения задачи 12. Решение. Выясним, являются ли векторы
Таким образом, из трех векторов 2) Разложим вектор Так как Так как Из
Таким образом,
Тогда
Задача 13. Найти ортогональную проекцию
Решение. Найдем базис в подпространстве
Составим таблицу значений переменных
Таким образом, фундаментальную систему решений (базис в подпространстве Далее задача решается аналогично задаче 12.
Определение 9. Величина
Задача 14. Найти расстояние от вектора x до подпространства Решение. Найдем
Задача 15. Найти расстояние от точки
Решение. Обозначим через
1. Построим базис линейного подпространства
Таким образом, базис в подпространстве Так как 2. Возьмем произвольную точку 3. Положим Так как Так как Таким образом,
|

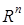 есть прямая сумма двух линейных подпространств:
есть прямая сумма двух линейных подпространств: 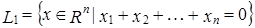 ,
, 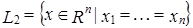 .
. – система векторов из X.
– система векторов из X. ,
,  называются базисными для системы векторов
называются базисными для системы векторов  .
. (
( ) образовывали базис в
) образовывали базис в 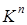 , необходимо и достаточно, чтобы определитель матрицы
, необходимо и достаточно, чтобы определитель матрицы  был отличен от нуля.
был отличен от нуля.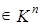 .
. ,
,  ,
, 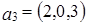 ,
, 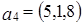 .
.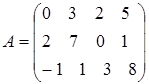 .
. ;
;  .
. , то данные векторы являются базисными векторами системы
, то данные векторы являются базисными векторами системы 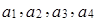 .
. =(1, 0, 0, -1),
=(1, 0, 0, -1), 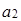 =(2, 1, 1, 0),
=(2, 1, 1, 0), 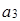 =(1, 1, 1, 1),
=(1, 1, 1, 1), 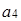 =(1, 2, 3, 4),
=(1, 2, 3, 4), =(0, 1, 2, 3);
=(0, 1, 2, 3);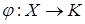 , обозначаемая
, обозначаемая  и удовлетворяющая следующим условиям:
и удовлетворяющая следующим условиям: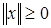 ,
,  ;
; ;
; ;
;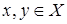 и любого числа
и любого числа  .
.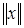 называется нормой вектора x.
называется нормой вектора x. (октаэдрическая норма);
(октаэдрическая норма); (кубическая норма)
(кубическая норма) (евклидова норма),
(евклидова норма),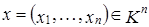 .
. выполняются аксиомы нормы.
выполняются аксиомы нормы. для любого
для любого  , то
, то 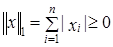 .Условие
.Условие  равносильно
равносильно 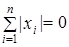 , а так как
, а так как 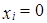 ,
,  , т.е.
, т.е.  .
. .
.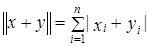 , а так как по свойству модуля
, а так как по свойству модуля 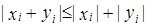 , то
, то 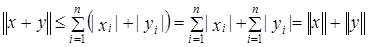 .
. является нормой в
является нормой в 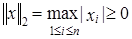 . Условие
. Условие  равносильно
равносильно 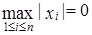
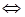
 , а так как, с другой стороны,
, а так как, с другой стороны, 
 , то получаем:
, то получаем: 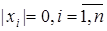 .
. .
. . Так как
. Так как  . Так как
. Так как 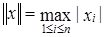 , то
, то  . Аналогично,
. Аналогично, 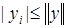 ,
, 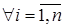 . Следовательно,
. Следовательно,  .
. является также нормой в пространстве
является также нормой в пространстве 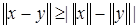 .
.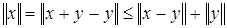 , следовательно,
, следовательно, 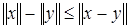 ;
;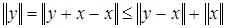 , следовательно,
, следовательно,  , а так как
, а так как 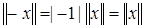 , то последнее неравенство преобразуется к виду:
, то последнее неравенство преобразуется к виду: 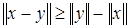 .
. , называемая скалярным произведением, ставящая в соответствие каждой паре векторов
, называемая скалярным произведением, ставящая в соответствие каждой паре векторов 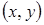 число
число  , причем для любых
, причем для любых 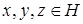 и
и 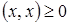 и
и  ;
;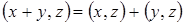 ;
;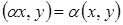 ;
; .
.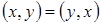 .
. .
.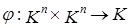
 задает скалярное произведение в
задает скалярное произведение в 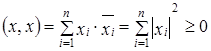 ;
; 
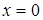 ;
; ;
; ;
; .
. задает скалярное произведение в
задает скалярное произведение в 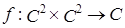 скалярное произведение в
скалярное произведение в 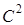 , если
, если 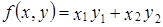 .
.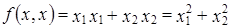 . Проверим выполнение неравенства
. Проверим выполнение неравенства 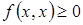 .
. :
: 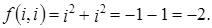 Так как
Так как 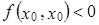 , то функция
, то функция 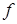 не является скалярным произведением.
не является скалярным произведением. – различные комплексные числа. Докажите, что в линейном пространстве
– различные комплексные числа. Докажите, что в линейном пространстве 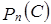 , где
, где  формула
формула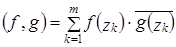 ,
, 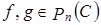 (*)
(*) ?
? :
: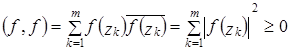 .
. . Тогда
. Тогда 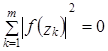 , т.е.
, т.е.  . Так как
. Так как  , а любой многочлен степени n однозначно определяется своими значениями в n+1 точке, то
, а любой многочлен степени n однозначно определяется своими значениями в n+1 точке, то  ;
; ;
;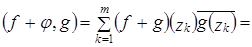
 .
.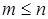 . Рассмотрим многочлен
. Рассмотрим многочлен  степени n, имеющий по основной теореме высшей алгебры n корней. Условие
степени n, имеющий по основной теореме высшей алгебры n корней. Условие  . Для данного многочлена выполнены условия:
. Для данного многочлена выполнены условия:  . Следовательно, при
. Следовательно, при  и
и 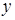 евклидова пространства H называется угол
евклидова пространства H называется угол 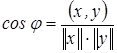 ,
, 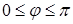 .
. и
и  .
. рассмотрим евклидову норму.
рассмотрим евклидову норму. ,
,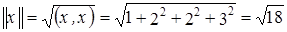 ,
,  . Тогда
. Тогда  , тогда
, тогда  .
.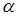 между функциями
между функциями 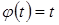 ,
, 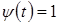 из пространства
из пространства  , если скалярное произведение задается следующей формулой:
, если скалярное произведение задается следующей формулой:  .
.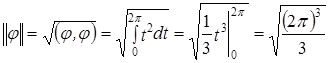 ,
, ,
, ,
,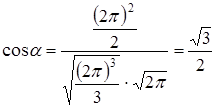

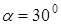 .
. называются ортогональными (перпендикулярными), если их скалярное произведение
называются ортогональными (перпендикулярными), если их скалярное произведение 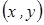 равно 0.
равно 0.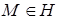 называется ортонормированной, если она ортогональна и в ней все векторы нормированы, т.е. выполняются условия:
называется ортонормированной, если она ортогональна и в ней все векторы нормированы, т.е. выполняются условия: ;
; .
. евклидова пространства H называется ортонормированным, если векторы
евклидова пространства H называется ортонормированным, если векторы  – линейно независимые векторы из H. Тогда векторы
– линейно независимые векторы из H. Тогда векторы 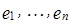 , определенные следующими равенствами:
, определенные следующими равенствами: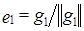 ,
,  ;
;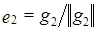 ,
,  ;
;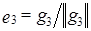 ,
,  ;
;
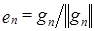 ,
, 
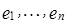 –ортонормированный базис в H, если H – конечномерно и
–ортонормированный базис в H, если H – конечномерно и  ,
, 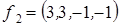 ,
,  .
.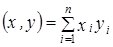 :
: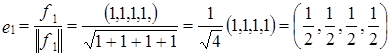 ;
;
 ;
; ;
; ;
; .
. ,
, 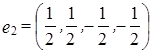 ,
, 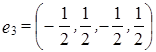 .
.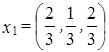 ,
,  образуют ортонормированное множество из
образуют ортонормированное множество из 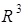 , и дополнить его до ортонормированного базиса.
, и дополнить его до ортонормированного базиса.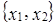 – ортонормированное.
– ортонормированное. ,
, 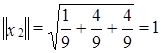 ;
;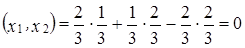 .
. , ортогональный к векторам
, ортогональный к векторам 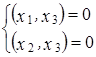

 .
.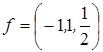 .
. .
. образуют ортонормированный базис в
образуют ортонормированный базис в  евклидова пространства
евклидова пространства 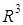 .
. ,
, 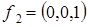
 – нормирован. Остается пронормировать вектор
– нормирован. Остается пронормировать вектор 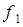 . Положим:
. Положим: ,
,  .
.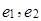 – ортонормированный базис в M.
– ортонормированный базис в M. ;
; 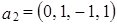 ;
;  .
. .
.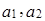 – линейно независимы, вектор
– линейно независимы, вектор 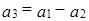 . Следовательно,
. Следовательно,  и
и  .
.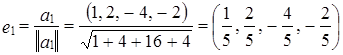 ;
;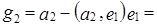
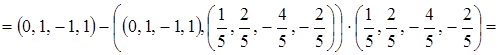
 =
= 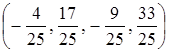 ;
; .
. ,
, 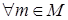 .
. всех векторов из H, каждый из которых ортогонален M.
всех векторов из H, каждый из которых ортогонален M. .
.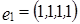 ,
,  .
. линейно независимы и образуют базис в M.
линейно независимы и образуют базис в M. ,
,  ,
, 

 .
.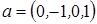 ,
, 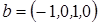 .
. . Поэтому для получения ортонормированного базиса остается только пронормировать a, b:
. Поэтому для получения ортонормированного базиса остается только пронормировать a, b: ,
,  .
. образуют ортонормированный базис в
образуют ортонормированный базис в  ,
,  ,
,  .
. .
. .
.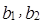 , принадлежащие
, принадлежащие  ,
, 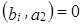 ,
,  . Задача сводится к нахождению фундаментальной системы решений для системы:
. Задача сводится к нахождению фундаментальной системы решений для системы: .
.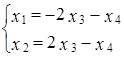 .
.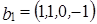 ,
, 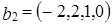 .
. ,
, 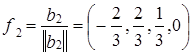 .
. на M, если вектор x-a перпендикулярен M.
на M, если вектор x-a перпендикулярен M. - ортонормированный базис в M. Тогда для любого вектора
- ортонормированный базис в M. Тогда для любого вектора 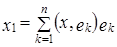
 на линейное подпространство L, натянутое на векторы:
на линейное подпространство L, натянутое на векторы:  ,
,  ,
,  .
. , следовательно,
, следовательно, 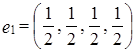 ,
,  .
. вектора x:
вектора x: =
=  .
. .
. ,
, 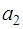 ,
,  линейно независимыми:
линейно независимыми: .
. два, например
два, например  , являются линейно независимыми. Их мы и возьмем в качестве базиса в подпространстве
, являются линейно независимыми. Их мы и возьмем в качестве базиса в подпространстве 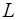 .
.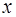 по векторам
по векторам 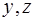 :
:  , где
, где 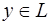 ,
,  .
. , где
, где  и
и  – некоторые константы, которые будут найдены в дальнейшем.
– некоторые константы, которые будут найдены в дальнейшем.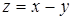 , то
, то  .
.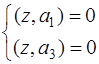 , поэтому
, поэтому

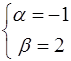 .
.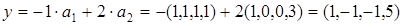 .
.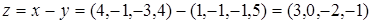 .
. и ортогональную составляющую
и ортогональную составляющую  вектора
вектора 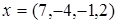 ,
,  .
.

 .
.



 ,
, 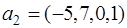 .
. , где a – проекция вектора x на подпространство M, называется расстоянием от вектора x до подпространства M.
, где a – проекция вектора x на подпространство M, называется расстоянием от вектора x до подпространства M.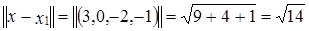 . Следовательно, расстояние от вектора x до подпространства
. Следовательно, расстояние от вектора x до подпространства 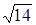 .
.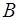 , заданной вектором
, заданной вектором  , до линейного многообразия, заданного системой уравнений:
, до линейного многообразия, заданного системой уравнений: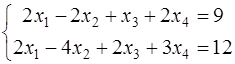 .
. – заданное линейное многообразие,
– заданное линейное многообразие, 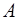 – некоторая точка линейного многообразия,
– некоторая точка линейного многообразия, 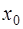 – задающий ее вектор,
– задающий ее вектор, 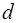 – расстояние от точки
– расстояние от точки  .
.
 . Составим таблицу значений переменных
. Составим таблицу значений переменных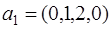 ,
,  .
. (коэффициенты
(коэффициенты  .
.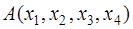 линейного многообразия
линейного многообразия 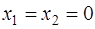 , тогда координаты
, тогда координаты  точки
точки 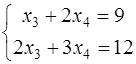 , откуда
, откуда 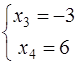 . Таким образом,
. Таким образом, 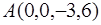 и, следовательно,
и, следовательно,  .
.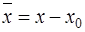 =(4,2,-5,1)-(0,0,-3,6)=(4,2,-2,-5). Пусть
=(4,2,-5,1)-(0,0,-3,6)=(4,2,-2,-5). Пусть  , где
, где 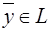 ,
, 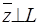 .
.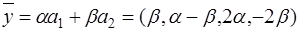 (коэффициенты
(коэффициенты 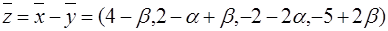 .
. , откуда следует, что
, откуда следует, что 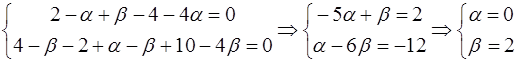 .
.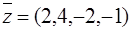 и, следовательно,
и, следовательно,  , то есть расстояние от точки
, то есть расстояние от точки 


