Метод наименьших квадратов для линейно сглаживающей функции.
Пусть измерены значения Yi функции Y(x) при заданных значениях аргумента xi (1< i < k); Y1 (х1), Y2 (х2),..., Yk (хk). Требуется найти функциональную зависимость, описывающую результаты эксперимента. Такая задача возникает в связи с тем, что наличие случайных погрешностей измерений делает бессмысленным подбор формулы, график которой должен обязательно проходить по всем точкам. Искомая функция должна лишь по возможности сгладить случайные погрешности эксперимента. Такая функция называется сглаживающей или выравнивающей. Выравнивание будет тем лучше. чем больше сделано измерений. Так. известно. что для проведения прямой достаточно двух точно известных точек Y1(х1) и Y2(х2), но при наличии погрешностей, для этой цели могут понадобиться десятки точек. Выбор сглаживающей функции делают обычно исходя из теоретических соображений или из упрощенного представления результатов измерений. Если выбранную функцию можно представить в виде Y = f(x, a, b, c,...), (1П)
то задача определения функции Y(х) сводится к определению параметров a,b,c,... Поскольку значения Yi содержит погрешности, то по ним нельзя точно определить параметры a, b, c,... Можно лишь получить достаточно хорошие оценки этих параметров. Наиболее прост для этогй цели метод наименьших квадратов, который заключается в следующем. Предположим, что измерения значений независимы, погрешности подчиняются нормальному закону распределения. Тогда для равноточных измерений оценки параметров a, b, c,... определяют из условия суммы квадратов отклонения измеренных значений от кривой
Для обеспечения минимума функции необходимо, чтобы ее частные производные первого порядка по параметрам a, b, c,... были равны нулю (
Тогда система (3П) будет линейной, т.к. параметры a, b, c,... входят линейно в выражение (1П). Данный случай выражает особый интерес в связи с тем, что на практике во многих случаях сложную функцию можно преобразовать в линейную. Итак, пусть имеется к измеренных значений Y1, Y2,..., Yk при соответственных значениях х1, х2,...,хk. Уравнение прямой представимо в виде Y=ax+b (4П)
Требуется подобрать коэффициенты a и b наилучшим образом. Для этого ищем минимум выражения
Продифференцируем эту формулу по параметрам a и b и приравняем производные к нулю
Следовательно, необходимо решить систему уравнений
Эта система уравнений называется нормальной. Решив ее, получим
По формулам (8П) и (9П) получим коэффициенты прямой линии. которая является лучшим приближением к искомой зависимости величин х и Y. Для удобства вычислений a и b применяется таблица 1П.
ЛИТЕРАТУРА. [1] А.П.Кондрашов, Е.В.Шестопалов. Основы физического эксперимента и математическая обработка результатов измерений. Атомиздат.М.1977 г. [2] Дж. Сквайрс. Практическая физика. М., Мир. 1971г.
ТАБЛИЦА 1П.
ЛАБОРАТОРНАЯ РАБОТА № 2
ОПРЕДЕЛЕНИЕ ВЯЗКОСТИ ВОЗДУХА И СРЕДНЕЙ ДЛИНЫ СВОБОДНОГО ПРОБЕГА МОЛЕКУЛ ВОЗДУХА.
ОБОРУДОВАНИЕ: установка ФПТ1-1, термометр, барометр.
Цель работы: ознакомиться с капиллярным методом определения вязкости, экспериментально определить вязкость воздуха и среднюю длину свободного пробега молекул воздуха, используя установку ФПТ1-1.
ТЕОРИЯ МЕТОДА ИЗМЕРЕНИЙ.
Вывод формулы Пуазейля.
Рассмотрим цилиндрический капилляр радиуса R и длины L, на концах которого поддерживаются давления Р1 и Р2, (Р1 > Р2). Найдем зависимость от времени объема газа, проходящего через капилляр, при условии, что обеспечивается ламинарный характер течения газа. Ось капилляра примем за ось Х, которую направим в сторону течения газа. В результате действия сил внутреннего трения, скорость течения газа в этом случае максимальна на оси цилиндрического капилляра и равна нулю у его стенок (рис.1), т.е. является функцией расстояния r, откладываемого от оси капилляра.
Рис.1.
Рис.2.
где f1 = f + df. Проекция на ось Х результирующей силы вязкого трения, действующей на внутренний слой, равна
При стационарном течении газа эта сила уравновешивается силой dF, направленной вдоль оси и создаваемой разностью давлений,
Таким образом
Данное выражение справедливо при любых значен6иях Х (не зависит от положения выбираемого цилиндрического слоя на оси Х). Это означает, что
Тогда выражение (4) принимает вид
После интегрирования
На оси трубы скорость течения газа максимальна, следовательно, Интегрируя
получаем зависимость
Значение постоянной интегрирования определяется из условия равенства скорости течения нулю на стенках капилляра, т.е. при r =R
Таким образом,
Через кольцевую площадку с внутренним радиусом r и толщиной dr (рис.2) за время t вытекает объем газа
Интегрируя это выражение по r в пределах от 0 до R, получим объем газа V1, протекшего за единицу времени через все сечение капилляра
Зная характеристики капилляра (R и L), разность давлений, поддерживаемую на его концах в ходе опыта и показания реометра (V1)- прибора для измерения объемного расхода газа, можно найти значение вязкости воздуха, при условии, конечно, что был обеспечен ламинарный характер протекания газа через капилляр.
Определение длины свободного пробега молекул воздуха.
Рассмотрим процесс возникновения вязкости (внутреннего трения) с точки зрения молекулярно-кинетической теории. Течение газа считаем ламинарным. В текущем газе на тепловую скорость движения молекул Выделим в газе площадку S, параллельную текущим с различными скоростями слоям (рис.3).
⅔
⅔
1
Рис.3 Слои, имеющие скорость упорядоченного движения u1 и u2, выберем лежащими под и над площадкой S на расстоянии средней длины свободного молекул в данном направлении (составляет ⅔ от
где
Соответственно, импульс, перенесенный из слоя 2
В результате импульс, перенесенный через площадку S за время Δt
Преобразуем разность скоростей слоев к виду
Или, т.к.
Знак «-» соответствует тому, что направление роста скорости u и направление передачи импульса упорядоченного движения противоположны. Сила, действующая со стороны более быстрого слоя на более медленный слой, равна
Сравнение с законом вязкого трения Ньютона (1) позволяет выразить вязкость η в виде
отсюда Так как
где Р - атмосферное давление, Т - абсолютная температура, μ - молекулярная масса газа, R - универсальная газовая постоянная. Зная вязкость, атмосферное давление и температуру газа, можем найти среднюю длину свободного пробега молекул воздуха. Описание установки. Используемая в данной работе установка ФПТ1-1 изображена на рис.4. Микрокомпрессор, установленный в приборном блоке 2, прокачивает воздух через металлический капилляр 4. Расход воздуха измеряется с помощью реометра 5
Установка ФПТ 1-1
1 - блок РЭ-1 2 - блок приборный БП – 1 3 - стойка РМС 4 - металлический капилляр 5 - реометр 6 - манометр
Рис.4.
Порядок выполнения работы.
1. Установить регулятор расхода воздуха «ВОЗДУХ» на минимум (крайнее левое положение) и включить тумблер «СЕТЬ». 2. Включить микрокомпрессор, плавно установить регулятор расхода воздуха в положение, соответствующее первому делению шкалы реометра (0,25*10-5 м3/с), и измерить разность давлений на концах капилляра с помощью манометра. 3. Повторить измерения при показаниях реометра, соответствующих расходу воздуха 0,5*10-5 м3/с (если это удастся). Каждое измерение проводится не менее 6 раз. 4. Вернуть регулятор «ВОЗДУХ» в крайнее левое положение, выключить микрокомпрессор и тумблер «СЕТЬ». 5. Для определения 6. Результаты измерений и обработки, данных эксперимента представить в виде двух таблиц – отдельно для η и отдельно для Вопросы. которые должны быть разобраны при подготовке к сдаче допуска к работе:
1.Объясните механизм возникновения внутреннего трения. 2. Выведите формулу Пуазейля. Каковы границы ее применения? 3. Каков реальный смысл характеристик капилляра R и L, входящих в формулу Пуазейля? 3. Выведите формулу Максвелла для вязкости (формула 10).
Вопросы. которые должны быть разобраны при подготовке к сдаче отчета.
1.Получите выражение (*), позволяющее находить среднюю длину свободного пробега молекул. 2. Выведете общее уравнение переноса и из него получите формулу 10. 3. Как зависит вязкость идеального газа от Р и Т? Литература. 1. Ф.Рейф. Статистическая физика. 1986 г.гл.8с.294-301. 2. Р.В.Телеснин. Молекулярная физика. М. «Высшая школа». 1973 г. 3. Д.В.Сивухин. Общий курс физики.т.1.Механика.1989г.§ 97.518-520 c. 4. А.Н.Матвеев. Молекулярная физика. М,"Высшая школа".1981г.355-361,363-366 с.
ЛАБОРАТОРНАЯ РАБОТА № 3 ОПРЕДЕЛЕНИЕ ПРИРАЩЕНИЯ ЭНТРОПИИ ТИОСУЛЬФАТА НАТРИЯ ПРИ НАГРЕВАНИИ.
ОБОРУДОВАНИЕ И МАТЕРМАЛЫ: пробирка с тиосульфатом натрия, термометр, электронагреватель, секундомер, термопара типа ХК, вольтметр цифровой. ЦЕЛЬ РАБОТЫ: научиться определять температуру плавления кристаллического вещества по графику зависимости температуры от времени нагрева; научиться определять приращение энтропии системы при изменении температуры и фазовых переходах первого рода; наблюдение метастабильного состояния (переохлажденной жидкости).
ТЕОРИЯ МЕТОДА ИЗМЕРЕНИЙ. В данной работе необходимо определить температуру плавления и приращение энтропии тиосульфата натрия (Na2S2O3·5H2O – тиосульфат пентагидрат натрия) при нагревании от комнатной температуры Тк до температуры плавления Тпл и его последующем плавлении до полностью расплавленного состояния. При поглощении системой, находящейся при температуре Т, малого количества теплоты
Приращение энтропии системы в процессе ее перехода из начального состояния О в конечное состояние N независимо от пути перехода можно определить так:
В нашем случае удобно отдельно рассматривать приращение энтропии ΔS, при нагреве системы от Тк до Тпл , и приращение энтропии системы ΔS2 при плавлении:
где с – удельная теплоемкость тиосульфата натрия, λ – удельная теплота плавления тиосульфата натрия, m – масса тиосульфата натрия. Температуру плавления кристаллического вещества можно определить по графику зависимости температуры тела от времени нагрева – пока вещество плавится, его температура не меняется, т.к. все тепло, поступающее от нагревателя, идет на разрушение связей в кристаллической решетке. При охлаждении тиосульфат легко переходит в метастабильное состояние – состояние переохлажденной жидкости (жидкость, имеющая температуру ниже температуры кристаллизации). В ходе эксперимента это состояние можно будет наблюдать достав пробирку из нагревателя после его выключения и проводя измерение температуру тиосульфата в режиме охлаждения вплоть до температур вблизи комнатной.
ИЗМЕРЕНИЯ И ОБРАБОТКА РЕЗУЛЬТАТОВ. Входящие в расчетные формулы константы для тиосульфата имеют значения: с = 360,7 Дж/(моль·К); λ = 23,4 кДж/моль; m= 2,5 г.
В данной работе для измерения температуры тиосульфата натрия используется термопара. Температура рабочего спая термопары фиксируется цифровым вольтметром в мB и затем с помощью таблицы переводится в t0 C. Температура свободных концов термопары фиксируется термометром и равна комнатной температуре. Подробнее о принципе измерения температуры с помощью термопары можно познакомиться в [3, 4] или в Приложении 2. Перед началом измерений определите, какие показания цифрового милливольтметра соответствуют температуре окончания нагрева (600С). Не забудьте при пользовании таблицей из Приложения 1 сделать поправку на то, что спай сравнения термопары находится не при 00С, а при комнатной температуре.
|

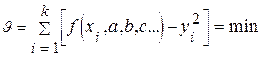 (2П)
(2П)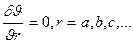 ), а частные производные второго порядка были положительны. При этом остальные параметры r полагаются постоянными. Следовательно, для определения параметров r = a, b, c,..., приводящих функцию к наименьшему значению, нужно решить систему уравнений
), а частные производные второго порядка были положительны. При этом остальные параметры r полагаются постоянными. Следовательно, для определения параметров r = a, b, c,..., приводящих функцию к наименьшему значению, нужно решить систему уравнений (3П) Решение этой системы уравнений покажем на примере функций, выражающей линейную зависимость между Y и х.
(3П) Решение этой системы уравнений покажем на примере функций, выражающей линейную зависимость между Y и х.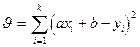 (5П)
(5П)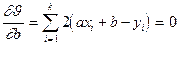 (6П)
(6П) 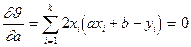
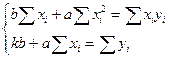 (7П)
(7П)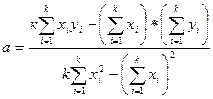 (8П)
(8П)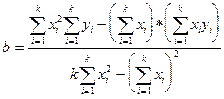 . (9П)
. (9П)
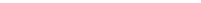
 Выделим в газе тонкий цили
Выделим в газе тонкий цили 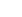 ндрический слой с радиусом внутрен
ндрический слой с радиусом внутрен 
 ней поверхности r, толщиной dr (рис.2)
ней поверхности r, толщиной dr (рис.2) 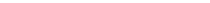 и длиной dL.
и длиной dL. 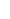 На внутреннюю поверхность слоя действует направленная вдоль оси Х сила
На внутреннюю поверхность слоя действует направленная вдоль оси Х сила  внутреннего трения
внутреннего трения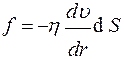 (1)
(1)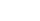

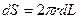 - площадь внутренней поверхности цилиндрического слоя,, h - вязкость газа, знак «-» учитывает, что с ростом r происходит уменьшение
- площадь внутренней поверхности цилиндрического слоя,, h - вязкость газа, знак «-» учитывает, что с ростом r происходит уменьшение 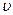 . На внешнюю поверхность действует тормозящая слой сила, модуль которой равен
. На внешнюю поверхность действует тормозящая слой сила, модуль которой равен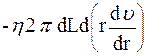 . (2)
. (2)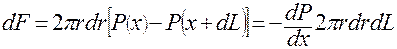 . (3)
. (3)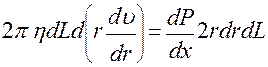
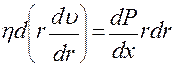 . (4)
. (4)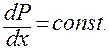 Учитывая, что давления на концах капилляра длиной L равны Р1 и Р2, получаем
Учитывая, что давления на концах капилляра длиной L равны Р1 и Р2, получаем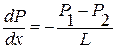 . (5)
. (5)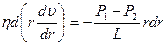 .
.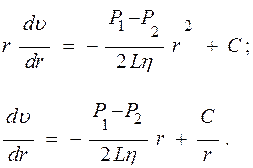
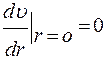 , из чего получаем, что С=0.
, из чего получаем, что С=0.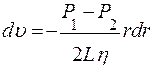 ,
,
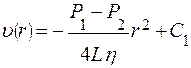
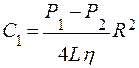 .
.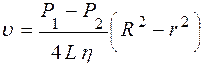 . (6)
. (6)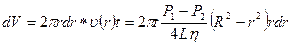 .
. (7) – формула Пуазейля.
(7) – формула Пуазейля.





 z 2
z 2 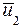

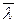



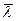 - средней длины свободного пробега). Тогда молекулы, движущиеся со стороны слоев к площадке, будут достигать ее в среднем без столкновений. Число молекул n1, пролетающих через площадку S со стороны слоя 1 за время Δt, равно
- средней длины свободного пробега). Тогда молекулы, движущиеся со стороны слоев к площадке, будут достигать ее в среднем без столкновений. Число молекул n1, пролетающих через площадку S со стороны слоя 1 за время Δt, равно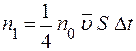 (8)
(8)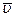 - средняя скорость теплового движения, n0 – концентрация молекул газа. Эти молекулы перенесут импульс упорядоченного движения
- средняя скорость теплового движения, n0 – концентрация молекул газа. Эти молекулы перенесут импульс упорядоченного движения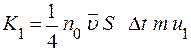 .
.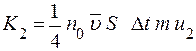 .
.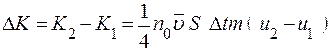 .
.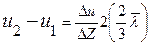 , тогда
, тогда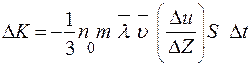 ,
,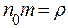 , то
, то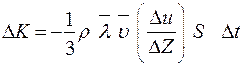 .
.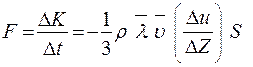 . (9)
. (9)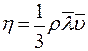 , (10)
, (10)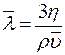 .
.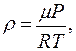
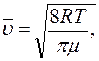
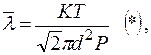 то
то , (11)
, (11)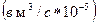 и может изменяться с помощью регулятора «ВОЗДУХ». Разность давлений на концах капилляра измеряется жидкостным манометром 6, колена которого подсоединены к отборным камерам, расположенным с разных концов капилляра. Длина капилляра 0,1 м, его внутренний диаметр 0,6 мм.
и может изменяться с помощью регулятора «ВОЗДУХ». Разность давлений на концах капилляра измеряется жидкостным манометром 6, колена которого подсоединены к отборным камерам, расположенным с разных концов капилляра. Длина капилляра 0,1 м, его внутренний диаметр 0,6 мм.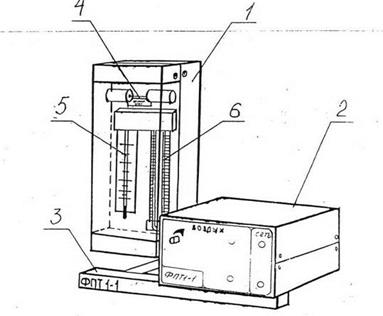
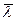 измерить температуру воздуха и атмосферное давление.
измерить температуру воздуха и атмосферное давление.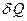 , энтропия системы испытывает приращение
, энтропия системы испытывает приращение (1)
(1)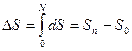 (2)
(2)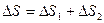 , (3)
, (3)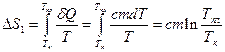 (4)
(4) (5)
(5)


