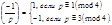35. Теорема о максимальном числе решений сравнения  -й степени по простому модулю. Теорема Вильсона.
-й степени по простому модулю. Теорема Вильсона.
Теорема 5. Сравнение степени  по простому модулю вида (1), где
по простому модулю вида (1), где 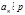 может иметь не более, чем
может иметь не более, чем  решений.
решений.
Доказательство. Пусть сравнение (1) имеет решение 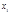 , т.е.
, т.е.  . Тогда по теореме Безу
. Тогда по теореме Безу 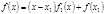 , где
, где  - многочлен с целыми коэффициентами степени
- многочлен с целыми коэффициентами степени  с неизменным старшим коэффициентом
с неизменным старшим коэффициентом 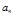 , а
, а  . Тогда получаем сравнение
. Тогда получаем сравнение  . (6)
. (6)
Таким образом, сравнение (1) эквивалентно сравнению 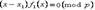 .
.
Аналогично можно получить тождественное сравнение  , если
, если 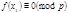 имеет решений
имеет решений 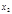 и т.д., пока не получим неразрешимое сравнение
и т.д., пока не получим неразрешимое сравнение
Возможны два случая.
В первом случае получаем тождественное сравнение  ,(7)
,(7)
которое показывает, что все найденные решения  для
для 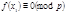 ,
,  , …,
, …,  являются также решениями сравнения Других решений (1) иметь не может, т.к. если
являются также решениями сравнения Других решений (1) иметь не может, т.к. если 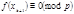 и
и  , то
, то 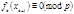 , т.к. остальные множители в (7) не делятся на
, т.к. остальные множители в (7) не делятся на  , что противоречит принятому условию о неразрешимости сравнения
, что противоречит принятому условию о неразрешимости сравнения 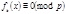 .
.
Во втором случае получаем тождественное сравнение  , которое аналогично не может иметь более
, которое аналогично не может иметь более  решений. Теорема доказана.
решений. Теорема доказана.
Следствие. Если сравнение (1) при отказе от требования 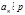 имеет более, чем
имеет более, чем  решений, то все коэффициенты
решений, то все коэффициенты 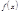 делятся на
делятся на  .
.
Теорема 6. Сравнение 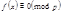 степени
степени 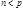 с коэффициентом 1 при старшем члене имеет
с коэффициентом 1 при старшем члене имеет  решений тогда и только тогда, когда все коэффициенты остатка от деления
решений тогда и только тогда, когда все коэффициенты остатка от деления  на
на 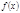 кратны
кратны 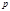 .
.
Доказательство Пусть 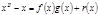 или
или 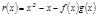 , (8)
, (8)
Причём 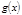
 имеют целые коэффициенты,
имеют целые коэффициенты,  ,
,  .
.
Пусть сравнение  имеет
имеет  решений, тогда
решений, тогда  имеет эти же
имеет эти же 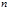 решений, т.к.
решений, т.к.  , но т.к.
, но т.к.  имеет степень
имеет степень 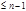 , то по следствию все коэффициенты
, то по следствию все коэффициенты 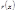 делятся на
делятся на 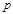 .
.
Обратно, пусть все коэффициенты  делятся на
делятся на 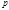 , тогда из (8) следует тождественная справедливость сравнения
, тогда из (8) следует тождественная справедливость сравнения 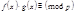 , т.е. оно имеет
, т.е. оно имеет 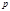 решений. Но любое решение этого сравнения удовлетворяет по крайней мере одному из сравнений
решений. Но любое решение этого сравнения удовлетворяет по крайней мере одному из сравнений  ,
,  имеет
имеет  решений, а сравнение
решений, а сравнение  имеет
имеет  решений. Тогда общее число решений этих сравнений
решений. Тогда общее число решений этих сравнений 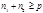 . Т.к.
. Т.к.  , то
, то 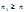 .
.
С другой стороны 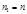 , т.е. сравнение
, т.е. сравнение 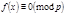 имеет ровно
имеет ровно  значений. Теорема доказана.
значений. Теорема доказана.
Теореме7 (Вильсона) Если 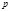 - простое число, то
- простое число, то 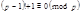 . (9)
. (9)
Доказательство. Сравнение  имеет
имеет  , т.е максимальное число решений. Эти решения
, т.е максимальное число решений. Эти решения 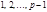 . Следовательно,
. Следовательно,  .
.
Подставим  :
:
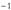
 или
или  .
.
Если 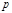 - нечётное, то
- нечётное, то  .
.
Если  , то
, то 
 - верно.
- верно.
Теорема доказана.
Замечание1. Для составного числа теорема Вильсона не верна.
Замечание2. Справедлива обратная теорема: Если для целого
положительного числа  имеет место соотношение (9), то
имеет место соотношение (9), то  - простое число. Однако этот критерий не имеет непосредственного применение на практике, т.к. для небольших
- простое число. Однако этот критерий не имеет непосредственного применение на практике, т.к. для небольших  число
число  очень большое.
очень большое.
36. Приведение сравнения n-й степени по составному модулю к системе сравнений. Приведение сравнения по составному
Теорема 8. Пусть 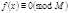 (10) и
(10) и 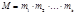 , где
, где  для
для  . Тогда сравнение (10) равносильно системе:
. Тогда сравнение (10) равносильно системе:
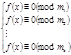 (11)
(11)
Доказательство.
1. Если сравнение имеет место по некоторому модулю  , то оно имеет место по любому модулю, являющимся делителем
, то оно имеет место по любому модулю, являющимся делителем  , т.е. если
, т.е. если  удовлетворяет (10), то удовлетворяет каждому сравнению (11).
удовлетворяет (10), то удовлетворяет каждому сравнению (11).
2. Если сравнение справедливо по модулям 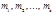 , то оно справедливо и по модулю равному
, то оно справедливо и по модулю равному  , т.к.
, т.к.  для
для  .
.
Замечание Если сравнение (10) имеет  решений, а отдельные сравнения системы (11) имеют
решений, а отдельные сравнения системы (11) имеют  , то
, то 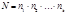 .
.
Рассмотрим Сравнение  (11)
(11)
Решать (11) методом подбора неудобно.
Сведём решение этого сравнения к сравнению по модулю р виде (1).. Действительно, всякое  , удовлетворяющее (11) удовлетворяет и (1), т.к. если
, удовлетворяющее (11) удовлетворяет и (1), т.к. если  , то
, то  .
.
Поэтому решение сравнения (11) надо искать среди решений сравнения (1). Сделаем это постепенно переходя от сравнения (1) к сравнению по модулю  . Пусть
. Пусть  или
или  . Где
. Где 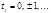 .
.
Выберем из (12) такие целые значения  .
.
Для вычисления левой части удобно заменить многочлен 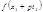 его разложением по формуле Тейлора
его разложением по формуле Тейлора 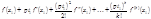 .
.





 За исключением первых двух слагаемых, все остальные содержат
За исключением первых двух слагаемых, все остальные содержат 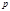 в степени
в степени 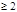 , следовательно
, следовательно  . Т.к.
. Т.к. 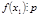 , то
, то 
 илb
илb  . (12)
. (12)
1 случай. Если  , то из (13)
, то из (13)  или
или 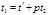 , где
, где 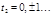 . Подставляя найденные
. Подставляя найденные  в (11) получаем
в (11) получаем 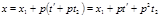 .(13)
.(13)
При 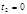 формула (13) даёт одно из решений сравнения
формула (13) даёт одно из решений сравнения  . Обозначим его через
. Обозначим его через 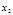 , тогда
, тогда  , где
, где  Или
Или 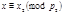 Переходя к решению сравнения
Переходя к решению сравнения 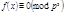 , (14) на
, (14) на  накладываем требование
накладываем требование  .
.
Далее применяем формулу Тейлора и процесс повторяем пока не придём к решению сравнения  . Итак, в случае
. Итак, в случае 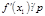 каждое решения сравнения (1) приводит к одному решению сравнения (11).
каждое решения сравнения (1) приводит к одному решению сравнения (11).
2 случай. Если 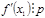 , а правая часть (12) на
, а правая часть (12) на  не делится, то сравнение (12), а значит и (11) не разрешимы.
не делится, то сравнение (12), а значит и (11) не разрешимы.
3 случай. Если 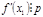 и правая часть (12) делится на
и правая часть (12) делится на 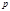 , то сравнение (12) тождественное и ему удовлетворяют все целые числа
, то сравнение (12) тождественное и ему удовлетворяют все целые числа  , тогда сравнение
, тогда сравнение  будет иметь
будет иметь 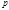 решений. Из этих решений будем далее общим приёмом выделять те числа, которые удовлетворяют сравнению по
решений. Из этих решений будем далее общим приёмом выделять те числа, которые удовлетворяют сравнению по 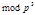 и т.д.
и т.д.
37 Сравнения второй степени, их связь с неопределёнными уравнениями второй степени с двумя неизвестными. Приведение Сравнений второй степени к двучленным сравнениям.
Определение. Сравнением второй степени называется сравнение вида 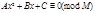 (1).
(1).
Сравнение второй степени (1) равносильно неопределённому уравнению второй степени вида 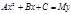
Определение. Двучленным сравнением второй степени называется сравнение вида 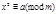 (3).
(3).
Сравнение второй степени (1) можно привести к двучленному сравнению (3).
Умножим обе части и модуль сравнения на  :
: 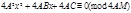 Дополним до полного квадрата:
Дополним до полного квадрата:  ,
, 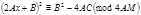 .
.
Обозначим  , тогда получаем двучленное сравнение
, тогда получаем двучленное сравнение 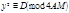 , (4)
, (4)
Каждое число, удовлетворяющее (1), будет также удовлетворять (4), поэтому из неразрешимости (4) следует неразрешимость (1). Однако, из разрешимости (4) относительно 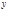 ещё не следует разрешимость (1) относительно
ещё не следует разрешимость (1) относительно 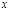 .
.
Действительно, каждое решение (4) 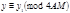 приводит к сравнению относительно
приводит к сравнению относительно 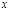
 или
или  т.к.
т.к.  , то если
, то если  , то сравнение (5),а следовательно и (1) не имеют решение. Если
, то сравнение (5),а следовательно и (1) не имеют решение. Если  , то сокращая обе части сравнения и модуль на
, то сокращая обе части сравнения и модуль на  , а для сравнения (1) необходимо указать решение по модулю
, а для сравнения (1) необходимо указать решение по модулю  , количество классов решений может уменьшиться.
, количество классов решений может уменьшиться.
38 Приведение Сравнений второй степени к двучленным сравнениям.
Определение. Сравнением второй степени называется сравнение вида 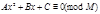 (1).
(1).
Сравнение второй степени (1) равносильно неопределённому уравнению второй степени вида 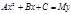
Определение. Двучленным сравнением второй степени называется сравнение вида 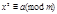 (3).
(3).
Сравнение второй степени (1) можно привести к двучленному сравнению (3).Умножим обе части и модуль сравнения на  :
: 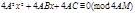 Дополним до полного квадрата:
Дополним до полного квадрата:  ,
, 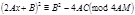 .Обозначим
.Обозначим 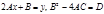 , тогда получаем двучленное сравнение
, тогда получаем двучленное сравнение 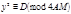 ,(4)
,(4)
Каждое число, удовлетворяющее (1), будет также удовлетворять (4), поэтому из неразрешимости (4) следует неразрешимость (1). Однако, из разрешимости (4) относительно  ещё не следует разрешимость (1) относительно
ещё не следует разрешимость (1) относительно 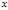 .Действительно, каждое решение (4)
.Действительно, каждое решение (4)  приводит к сравнению относительно
приводит к сравнению относительно 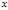
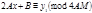 или
или  (5)
(5)
т.к.  , то если
, то если 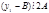 , то сравнение (5),а следовательно и (1) не имеют решение. Если
, то сравнение (5),а следовательно и (1) не имеют решение. Если  , то сокращая обе части сравнения и модуль на
, то сокращая обе части сравнения и модуль на 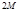 , а для сравнения (1) необходимо указать решение по модулю
, а для сравнения (1) необходимо указать решение по модулю 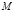 , количество классов решений может уменьшиться.
, количество классов решений может уменьшиться.
39 Двучленные сравнения по простому модулю: квадратные вычеты и невычеты, критерий Эйлера.
Пусть дано двучленное сравнение (3):  и
и  .
.
Определение. Если сравнение (3) разрешимо, то  называется квадратичным вычетом по модулю
называется квадратичным вычетом по модулю 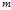 . Если сравнение (3) неразрешимо, то
. Если сравнение (3) неразрешимо, то 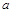 называется квадратичным невычетом по модулю
называется квадратичным невычетом по модулю 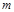 .
.
Рассмотрим двучленное сравнение по нечётному простому модулю.
Пусть дано сравнение:  ,
,
где 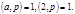 Тогда решение этого сравнения следует искать среди чисел приведённой системы вычетов по модулю
Тогда решение этого сравнения следует искать среди чисел приведённой системы вычетов по модулю  .
.
Если сравнение (6) имеет решения  , то оно должно также иметь решения
, то оно должно также иметь решения 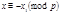 .
.
Причём сравнение второй степени по простому модулю не может иметь более 2-ч решений. Для отыскания решений будем испытывать приведённую систему абсолютно наименьших вычетов 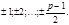 Для отыскания решений достаточно подставлять в (6) только положительные значения
Для отыскания решений достаточно подставлять в (6) только положительные значения 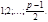 При этом в левой части получаются числа
При этом в левой части получаются числа 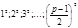 (7)
(7)
Разрешимыми будут только такие сравнения (6), в которых число  сравнимо с одним из чисел ряда (7). Таким образом, ряд (7) состоит из квадратичных вычетов по
сравнимо с одним из чисел ряда (7). Таким образом, ряд (7) состоит из квадратичных вычетов по 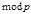 . Таким образом, количество квадратичных вычетов из разных классов по модулю
. Таким образом, количество квадратичных вычетов из разных классов по модулю 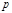 равно
равно  Очевидно, число квадратичных невычетов тоже равно
Очевидно, число квадратичных невычетов тоже равно 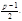
Теорема (критерий Эйлера) Число  , которое не делится на нечётное простое число
, которое не делится на нечётное простое число 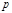 , является квадратичным вычетом по модулю
, является квадратичным вычетом по модулю 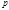 тогда и только тогда, когда
тогда и только тогда, когда 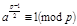 , (8)
, (8)
и квадратичным невычетом тогда и только тогда, когда  . (9)
. (9)
Доказательство По теореме Ферма, т.к.  , то
, то  , т.к.
, т.к.  , то
, то  , следовательно
, следовательно 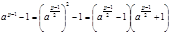 . Тогда
. Тогда  .Отсюда, по крайне мере, одна из скобок делится на
.Отсюда, по крайне мере, одна из скобок делится на 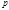 . Однако обе скобки делится на
. Однако обе скобки делится на  не могут, т.к. в этом случае разность
не могут, т.к. в этом случае разность  должна делится на
должна делится на  , но
, но 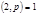 по условию. Если
по условию. Если  - квадратичный невычет, то
- квадратичный невычет, то 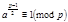 . Действительно в этом случае существует такое значение
. Действительно в этом случае существует такое значение 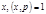 , что
, что  , откуда
, откуда 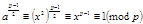 . Так как сравнение (8) не может иметь более
. Так как сравнение (8) не может иметь более 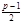 решений, то оно выполняется только для всех квадратичных вычетов. Но тогда для остальных
решений, то оно выполняется только для всех квадратичных вычетов. Но тогда для остальных  ,
,  , т.е. для квадратичных невычетов
, т.е. для квадратичных невычетов  , т.е. выполнено условие (9):
, т.е. выполнено условие (9):  .
.
40 Символ Лежандра и его свойства. Закон взаимности квадратичных вычетов.
Определение Пусть 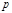 - нечётное простое число и
- нечётное простое число и  не делится на
не делится на  . Символ Лежандра называется символ вида
. Символ Лежандра называется символ вида  Читается
Читается 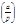 - «символ Лежандра
- «символ Лежандра  по отношению к
по отношению к  »,
»,  - числитель,
- числитель, 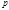 - знаменатель символа.
- знаменатель символа.
Свойства символа Лежандра:
10. Если 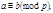 то
то  .
.
20. 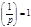 , т.е. 1 – квадратичный вычет для любого нечётного простого
, т.е. 1 – квадратичный вычет для любого нечётного простого 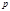 , т.к. сравнение
, т.к. сравнение 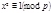 всегда разрешимо.
всегда разрешимо.
30. 
Следствие. 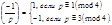

 -й степени по простому модулю. Теорема Вильсона.
-й степени по простому модулю. Теорема Вильсона. 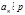 может иметь не более, чем
может иметь не более, чем  решений.
решений. 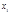 , т.е.
, т.е.  . Тогда по теореме Безу
. Тогда по теореме Безу 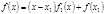 , где
, где  - многочлен с целыми коэффициентами степени
- многочлен с целыми коэффициентами степени  с неизменным старшим коэффициентом
с неизменным старшим коэффициентом 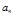 , а
, а  . Тогда получаем сравнение
. Тогда получаем сравнение  . (6)
. (6)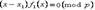 .
. , если
, если 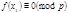 имеет решений
имеет решений 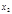 и т.д., пока не получим неразрешимое сравнение
и т.д., пока не получим неразрешимое сравнение ,(7)
,(7) для
для 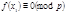 ,
,  , …,
, …,  являются также решениями сравнения Других решений (1) иметь не может, т.к. если
являются также решениями сравнения Других решений (1) иметь не может, т.к. если 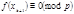 и
и  , то
, то 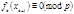 , т.к. остальные множители в (7) не делятся на
, т.к. остальные множители в (7) не делятся на  , что противоречит принятому условию о неразрешимости сравнения
, что противоречит принятому условию о неразрешимости сравнения 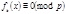 .
. , которое аналогично не может иметь более
, которое аналогично не может иметь более  решений, то все коэффициенты
решений, то все коэффициенты 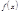 делятся на
делятся на  .
.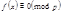 степени
степени 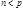 с коэффициентом 1 при старшем члене имеет
с коэффициентом 1 при старшем члене имеет  решений тогда и только тогда, когда все коэффициенты остатка от деления
решений тогда и только тогда, когда все коэффициенты остатка от деления  на
на 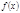 кратны
кратны 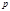 .
.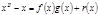 или
или 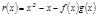 , (8)
, (8)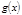
 имеют целые коэффициенты,
имеют целые коэффициенты,  ,
,  .
. имеет
имеет  решений, тогда
решений, тогда  имеет эти же
имеет эти же 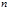 решений, т.к.
решений, т.к.  , но т.к.
, но т.к.  имеет степень
имеет степень 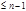 , то по следствию все коэффициенты
, то по следствию все коэффициенты 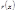 делятся на
делятся на 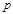 .
.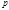 , тогда из (8) следует тождественная справедливость сравнения
, тогда из (8) следует тождественная справедливость сравнения 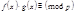 , т.е. оно имеет
, т.е. оно имеет  ,
,  имеет
имеет  решений, а сравнение
решений, а сравнение  имеет
имеет  решений. Тогда общее число решений этих сравнений
решений. Тогда общее число решений этих сравнений 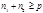 . Т.к.
. Т.к.  , то
, то 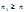 .
.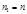 , т.е. сравнение
, т.е. сравнение 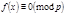 имеет ровно
имеет ровно 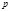 - простое число, то
- простое число, то 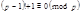 . (9)
. (9) имеет
имеет  , т.е максимальное число решений. Эти решения
, т.е максимальное число решений. Эти решения 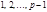 . Следовательно,
. Следовательно,  .
. :
: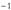
 или
или  .
.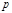 - нечётное, то
- нечётное, то  .
. , то
, то 
 - верно.
- верно. - простое число. Однако этот критерий не имеет непосредственного применение на практике, т.к. для небольших
- простое число. Однако этот критерий не имеет непосредственного применение на практике, т.к. для небольших  очень большое.
очень большое.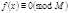 (10) и
(10) и 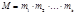 , где
, где  для
для  . Тогда сравнение (10) равносильно системе:
. Тогда сравнение (10) равносильно системе: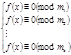 (11)
(11) , то оно имеет место по любому модулю, являющимся делителем
, то оно имеет место по любому модулю, являющимся делителем  , т.е. если
, т.е. если  удовлетворяет (10), то удовлетворяет каждому сравнению (11).
удовлетворяет (10), то удовлетворяет каждому сравнению (11).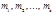 , то оно справедливо и по модулю равному
, то оно справедливо и по модулю равному  , т.к.
, т.к.  для
для  .
. решений, а отдельные сравнения системы (11) имеют
решений, а отдельные сравнения системы (11) имеют  , то
, то 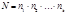 .
. (11)
(11) , удовлетворяющее (11) удовлетворяет и (1), т.к. если
, удовлетворяющее (11) удовлетворяет и (1), т.к. если  , то
, то  .
. . Пусть
. Пусть  или
или  . Где
. Где 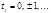 .
. .
.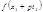 его разложением по формуле Тейлора
его разложением по формуле Тейлора 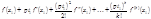 .
.

 За исключением первых двух слагаемых, все остальные содержат
За исключением первых двух слагаемых, все остальные содержат 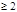 , следовательно
, следовательно  . Т.к.
. Т.к. 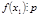 , то
, то 
 илb
илb  . (12)
. (12) , то из (13)
, то из (13)  или
или 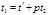 , где
, где 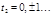 . Подставляя найденные
. Подставляя найденные  в (11) получаем
в (11) получаем 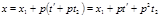 .(13)
.(13)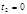 формула (13) даёт одно из решений сравнения
формула (13) даёт одно из решений сравнения  . Обозначим его через
. Обозначим его через 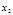 , тогда
, тогда  , где
, где  Или
Или 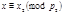 Переходя к решению сравнения
Переходя к решению сравнения 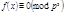 , (14) на
, (14) на  накладываем требование
накладываем требование  .
. . Итак, в случае
. Итак, в случае 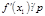 каждое решения сравнения (1) приводит к одному решению сравнения (11).
каждое решения сравнения (1) приводит к одному решению сравнения (11).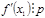 , а правая часть (12) на
, а правая часть (12) на  не делится, то сравнение (12), а значит и (11) не разрешимы.
не делится, то сравнение (12), а значит и (11) не разрешимы.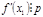 и правая часть (12) делится на
и правая часть (12) делится на  , тогда сравнение
, тогда сравнение  будет иметь
будет иметь 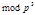 и т.д.
и т.д.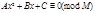 (1).
(1).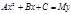
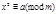 (3).
(3). :
: 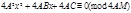 Дополним до полного квадрата:
Дополним до полного квадрата:  ,
, 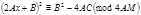 .
. , тогда получаем двучленное сравнение
, тогда получаем двучленное сравнение 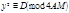 , (4)
, (4)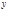 ещё не следует разрешимость (1) относительно
ещё не следует разрешимость (1) относительно 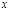 .
.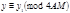 приводит к сравнению относительно
приводит к сравнению относительно  или
или  т.к.
т.к.  , то если
, то если  , то сравнение (5),а следовательно и (1) не имеют решение. Если
, то сравнение (5),а следовательно и (1) не имеют решение. Если  , то сокращая обе части сравнения и модуль на
, то сокращая обе части сравнения и модуль на  , а для сравнения (1) необходимо указать решение по модулю
, а для сравнения (1) необходимо указать решение по модулю  , количество классов решений может уменьшиться.
, количество классов решений может уменьшиться.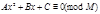 (1).
(1).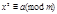 (3).
(3). :
: 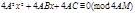 Дополним до полного квадрата:
Дополним до полного квадрата:  ,
, 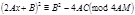 .Обозначим
.Обозначим 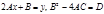 , тогда получаем двучленное сравнение
, тогда получаем двучленное сравнение 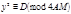 ,(4)
,(4) ещё не следует разрешимость (1) относительно
ещё не следует разрешимость (1) относительно 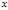 .Действительно, каждое решение (4)
.Действительно, каждое решение (4)  приводит к сравнению относительно
приводит к сравнению относительно 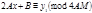 или
или  (5)
(5)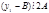 , то сравнение (5),а следовательно и (1) не имеют решение. Если
, то сравнение (5),а следовательно и (1) не имеют решение. Если  , то сокращая обе части сравнения и модуль на
, то сокращая обе части сравнения и модуль на 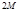 , а для сравнения (1) необходимо указать решение по модулю
, а для сравнения (1) необходимо указать решение по модулю 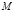 , количество классов решений может уменьшиться.
, количество классов решений может уменьшиться. и
и  .
. называется квадратичным вычетом по модулю
называется квадратичным вычетом по модулю 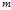 . Если сравнение (3) неразрешимо, то
. Если сравнение (3) неразрешимо, то 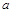 называется квадратичным невычетом по модулю
называется квадратичным невычетом по модулю 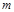 .
.  ,
, 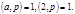 Тогда решение этого сравнения следует искать среди чисел приведённой системы вычетов по модулю
Тогда решение этого сравнения следует искать среди чисел приведённой системы вычетов по модулю  , то оно должно также иметь решения
, то оно должно также иметь решения 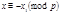 .
.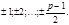 Для отыскания решений достаточно подставлять в (6) только положительные значения
Для отыскания решений достаточно подставлять в (6) только положительные значения 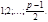 При этом в левой части получаются числа
При этом в левой части получаются числа 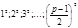 (7)
(7) сравнимо с одним из чисел ряда (7). Таким образом, ряд (7) состоит из квадратичных вычетов по
сравнимо с одним из чисел ряда (7). Таким образом, ряд (7) состоит из квадратичных вычетов по 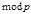 . Таким образом, количество квадратичных вычетов из разных классов по модулю
. Таким образом, количество квадратичных вычетов из разных классов по модулю  Очевидно, число квадратичных невычетов тоже равно
Очевидно, число квадратичных невычетов тоже равно 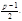
 , которое не делится на нечётное простое число
, которое не делится на нечётное простое число 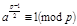 , (8)
, (8)  . (9)
. (9) , то
, то  , т.к.
, т.к.  , то
, то  , следовательно
, следовательно 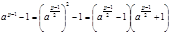 . Тогда
. Тогда  .Отсюда, по крайне мере, одна из скобок делится на
.Отсюда, по крайне мере, одна из скобок делится на  должна делится на
должна делится на  , но
, но 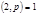 по условию. Если
по условию. Если 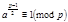 . Действительно в этом случае существует такое значение
. Действительно в этом случае существует такое значение 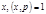 , что
, что  , откуда
, откуда 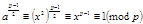 . Так как сравнение (8) не может иметь более
. Так как сравнение (8) не может иметь более 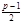 решений, то оно выполняется только для всех квадратичных вычетов. Но тогда для остальных
решений, то оно выполняется только для всех квадратичных вычетов. Но тогда для остальных  ,
,  , т.е. для квадратичных невычетов
, т.е. для квадратичных невычетов  , т.е. выполнено условие (9):
, т.е. выполнено условие (9):  .
. не делится на
не делится на  Читается
Читается 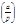 - «символ Лежандра
- «символ Лежандра  »,
», 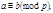 то
то  .
.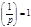 , т.е. 1 – квадратичный вычет для любого нечётного простого
, т.е. 1 – квадратичный вычет для любого нечётного простого 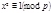 всегда разрешимо.
всегда разрешимо.