Рівняння Лагранжа. Функція Лагранжа.У цьому параграфі ми викладемо такий спосіб розв’язку основної динамічної задачі для механічних систем з в’язями, який не містить недоліків способу викладеного в § 12. Основна ідея полягає в тому, щоб загальну динамічну задачу про відшукання закону руху системи і сил реакції в'язів Для виключення сил реакцій в'язів, помножимо скалярно кожне з рівнянь руху (12,11) на віртуальне переміщення
В силу умови ідеальності в'язів (12,10) остання сума в (13,1) обертається в нуль, тому перепишемо (13,1) у вигляді:
Рівняння (13,2) являє собою математичне формулювання одного з найважливіших диференціальних варіаційних принципів механіки – принципу Д’Аламбера – Лагранжа, що стверджує: якщо на механічну систему накладені утримуючі, голономні й ідеальні в'язі, то в кожен момент часу сума віртуальних робіт всіх активних сил Рівняння (13,2) містять варіації Узагальненими (або незалежними) координатами механічної системи називають будь-які 3n-k величин 1) Декартові координати точок повинні бути однозначними функціями узагальнених координат вигляду:
якщо на систему накладені нестаціонарні в'язі, або в'язі вигляду:
якщо на систему накладені стаціонарні в'язі. 2) Узагальнені координати необхідно вибирати в повній відповідності з накладеними на систему в'язями. Це означає, що рівняння в'язів (12,2) повинні обертатися в тотожність при підстановці в них функцій (13,3) або (13,4). Пояснимо сказане на прикладі сферичного маятника, розглянутого в § 12. Для цієї системи n=1, k=1, тому s=3n–k=2, тобто положення маятника можна задати за допомогою двох узагальнених координат, у якості яких можна вибрати сферичні координати θ і φ. При цьому декартові координати однозначно виражаються через θ і φ:
а рівняння в'язів (12,17) обертається в тотожність при підстановці в нього функції (13,5), що легко перевірити. Зауваження. В §6 ми бачили, що станвільної системи в будь-який момент часу визначається одночасним заданням її декартових координат Випишемо тут ряд формул, якими ми надалі скористаємося, описуючи перехід від декартових координат до узагальнених. Для віртуальних переміщень із (13,3) маємо:
де
Так як згідно (13,6) швидкості
Далі, з огляду на те, що
таким чином остаточно маємо тотожності:
Перейдемо тепер у рівнянні (13,2) до узагальнених координат. Підставляючи в (13,2) вираження (13,5) і змінюючи порядок виконання операцій підсумовуванням по індексах i та α;, одержуємо:
Уведемо позначення:
і назвемо скалярну величину
Це і є, по суті справи, шукані рівняння руху в узагальнених координатах, де
звідки з урахуванням тотожностей (13,7) - (13,8) одержуємо:
і, отже,
де З врахуванням (13.12) перепишемо рівняння (13.11) в остаточному вигляді:
Ці рівняння називаються рівняннями Лагранжа другого роду або просто рівняннями Лагранжа. Вони справедливі для будь-якої механічної системи з ідеальними голономними й утримуючими в'язями. Невідомими в цих рівняннях є функції Методика застосування рівнянь Лагранжа до розв’язку конкретних задач складається з наступних кроків: 1) вибираються узагальнені координати системи 2) знаходиться явний вираз для 3) складаються рівняння (13.13) у явному вигляді (після підстановки 4) інтегруючи ці рівняння й визначаючи сталі інтегрування по початковим або крайовим умовам, знаходять залежності Зауваження 1. Рівняння Лагранжа (13.13) мають велике значення також і для динаміки вільних механічних систем, стосовно яких вони збігаються з рівняннями руху Ньютона, записаними в довільній (залежної від вибору узагальнених координат) системі криволінійних координат (доведення цього твердження ми опускаємо). Зауваження 2. Варто мати на увазі, що вибір узагальнених координат системи неоднозначний: якщо q й
Перетворення (13.14) від одного набору узагальнених координат q до іншого набору
Ясно, що якщо тепер переходити в рівнянні (13.12) до узагальнених координат за допомогою (13.15), то одержимо рівняння Лагранжа тієї ж форми, що й (13.13), але тільки в штрихованих координатах. Таким чином, рівняння Лагранжа інваріантні відносно точкових перетворень (13.14). Дослідимо тепер більш докладно структуру рівнянь Лагранжа (13.13) для різних класів (див. § 7) механічних систем. Ця структура визначається конкретним виглядом узагальнених сил Нехай всі активні сили
де
З урахуванням (13.16) і (13.17) рівняння Лагранжа (13.13) можна представити у вигляді:
або
де функція узагальнених координат
називається функцією Лагранжа механічної системи. Хоча тут функцію Лагранжа (13.19) ми ввели формальним чином з метою запису рівнянь Лагранжа (13.13) для механічних систем з потенціальними активними силами у формі (13.18), однак в § 14 ми покажемо, що
Зауваження 1. Легко переконатися, що до вигляду (13.18) рівняння Лагранжа (13.13) приводяться також і для класу механічних систем з узагальнено-потенціальними силами, тобто для таких систем, узагальнені сили
де
Найважливішим прикладом системи з узагальнено-потенційними силами є система заряджених часток, що рухаються в зовнішньому електромагнітному полі. Наприклад, у вигляді (13.20) можна представити силу Лоренца (див. частина II цього курсу). Зауваження 2. Якщо на механічну систему поряд з потенційними (або узагальнено-потенційними) активними силами діють і дисипативні сили (тобто сили системи, що приводять до розсіювання механічної енергії,), то при записі рівнянь Лагранжа (13.13) діють таким чином. Кожну узагальнену силу
де - узагальнені сили, обумовлені дією на систему тільки потенціальних (або узагальнено-потенціальних) сил, і:
- узагальнені сили, що виникають у результаті дії на систему не потенціальних дисипативних сил в’язкого тертя. Легко бачити, що рівняння Лагранжа (13.13) у цьому випадку можна представити у вигляді:
де
Розглянемо тепер структуру кінетичної енергії Дійсно, підставляючи (13.6) у визначення
де
Таким чином, з (13.25) – (13.28) видно, що не стаціонарність в'язів, що накладаються на механічну систему, приводить до двох ефектів: 1) У випадку, коли на систему накладені тільки стаціонарні в'язі, а всі активні сили, що діють на неї, є потенційними, то
Так як математичне зауваження. Якщо
Дійсно, функція
Диференціюючи (13.31) по
Полягаючи тут, що На підставі теореми Ейлера (13.30) для кінетичної енергії
якою ми надалі скористаємося. Зауваження. Найважливіше значення рівнянь Лагранжа у формі (13.18) полягає в тому, що при відповідному узагальненні понять їх можна використовувати не тільки в механіці, але й в інших розділах фізики, наприклад для вивчення руху класичних фізичних полів, тобто систем з нескінченним числом ступенів свободи.
|

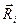 розбити (розчленувати) на дві задачі: 1) знайти спочатку закон руху системи (цю задачу надалі ми й будемо називати основною); для цього необхідно одержати замкнуту систему рівнянь для S =3n-k незалежних координат системи (за допомогою яких можна задати стан системи з в’язями в будь-який момент часу); 2) потім за допомогою рівнянь (12,11) визначити й невідомі
розбити (розчленувати) на дві задачі: 1) знайти спочатку закон руху системи (цю задачу надалі ми й будемо називати основною); для цього необхідно одержати замкнуту систему рівнянь для S =3n-k незалежних координат системи (за допомогою яких можна задати стан системи з в’язями в будь-який момент часу); 2) потім за допомогою рівнянь (12,11) визначити й невідомі  відповідної точки й складемо почленно результати множення. Одержуємо рівняння:
відповідної точки й складемо почленно результати множення. Одержуємо рівняння: (13,1)
(13,1) (13,2)
(13,2) і так званих “ сил інерції ” Д’Аламбера
і так званих “ сил інерції ” Д’Аламбера  дорівнює нулю для будь-якого віртуального переміщення системи. Рівняння (13,2) називають також загальним рівнянням динаміки голономних систем, тому що його можна прийняти в якості основної і єдиної аксіоми для побудови теорії руху таких систем (з нього можна одержати будь-які інші рівняння руху, тобто такі, як рівняння Ньютона, так і рівняння Лагранжа).
дорівнює нулю для будь-якого віртуального переміщення системи. Рівняння (13,2) називають також загальним рівнянням динаміки голономних систем, тому що його можна прийняти в якості основної і єдиної аксіоми для побудови теорії руху таких систем (з нього можна одержати будь-які інші рівняння руху, тобто такі, як рівняння Ньютона, так і рівняння Лагранжа). (число яких збігається із числом ступенів свободи системи s=3n-k), що однозначно визначають положення системи в просторі в будь-який момент часу. Із цього визначення випливає, що узагальнені координати повинні задовольняти наступним двом вимогам:
(число яких збігається із числом ступенів свободи системи s=3n-k), що однозначно визначають положення системи в просторі в будь-який момент часу. Із цього визначення випливає, що узагальнені координати повинні задовольняти наступним двом вимогам: , (13,3)
, (13,3) , (13,4)
, (13,4) , (13,5)
, (13,5)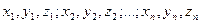 і декартових компонент швидкостей точок
і декартових компонент швидкостей точок 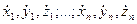 . Аналогічно, стан системи з в’язями в будь-який момент часу повністю визначається одночасним завданням її узагальнених координат
. Аналогічно, стан системи з в’язями в будь-який момент часу повністю визначається одночасним завданням її узагальнених координат  . Ясно, що фізично таке визначення стану системи засновано на допущенні про можливості одночасного точного виміру в макроскопічних тілах будь-яких фізичних величин (див. §6).
. Ясно, що фізично таке визначення стану системи засновано на допущенні про можливості одночасного точного виміру в макроскопічних тілах будь-яких фізичних величин (див. §6). , (13,5)
, (13,5)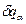 - варіації узагальнених (незалежних) координат. Зв'язок між швидкостями точок
- варіації узагальнених (незалежних) координат. Зв'язок між швидкостями точок 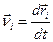 й їхніми узагальненими швидкостями
й їхніми узагальненими швидкостями 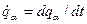 одержуємо, диференціюючи (13,3) за часом:
одержуємо, диференціюючи (13,3) за часом: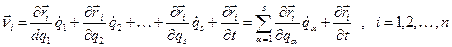 . (13,6)
. (13,6) є лінійні функції узагальнених швидкостей
є лінійні функції узагальнених швидкостей  , то беручи часткові похідні по
, то беручи часткові похідні по  . (13.7)
. (13.7) є функції узагальнених координат
є функції узагальнених координат  і часу t, та використовуючи (13,6) одержуємо:
і часу t, та використовуючи (13,6) одержуємо:
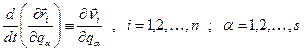 . (13,8)
. (13,8)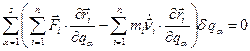 (13,9)
(13,9) (13,10)
(13,10)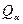 узагальненою силою, що відповідає незалежній координаті
узагальненою силою, що відповідає незалежній координаті 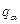 . Так як віртуальні переміщення
. Так як віртуальні переміщення  незалежні, то всі коефіцієнти при всіх переміщеннях у лівій частині рівності (13,9) повинні обертатися в нуль, тобто з врахуванням (13,10) маємо рівняння:
незалежні, то всі коефіцієнти при всіх переміщеннях у лівій частині рівності (13,9) повинні обертатися в нуль, тобто з врахуванням (13,10) маємо рівняння: (13,11)
(13,11) й
й  згідно (13,3) і (13,6) варто розглядати як функції узагальнених координат і швидкостей:
згідно (13,3) і (13,6) варто розглядати як функції узагальнених координат і швидкостей: 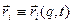 ,
,  . Тут і надалі ми скористаємося скороченими позначеннями:
. Тут і надалі ми скористаємося скороченими позначеннями: 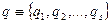 і
і  . Для кращого розуміння фізичного змісту величини, що є в лівій частині (13,11), проробимо з нею ряд тотожних перетворень. Насамперед помітимо, що:
. Для кращого розуміння фізичного змісту величини, що є в лівій частині (13,11), проробимо з нею ряд тотожних перетворень. Насамперед помітимо, що: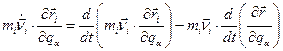

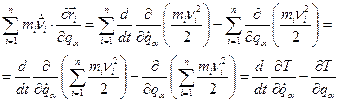 (13.12)
(13.12) - кінетична енергія системи, представлена як функція узагальнених координат
- кінетична енергія системи, представлена як функція узагальнених координат 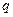 , узагальнених швидкостей
, узагальнених швидкостей 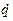 і часу
і часу 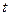 .
.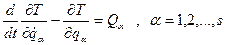 . (13.13)
. (13.13)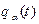 , які однозначно визначають положення системи в просторі (причому число невідомих дорівнює числу рівнянь). Велика перевага рівнянь Лагранжа полягає в тому, що їхнє число дорівнює числу ступенів свободи системи й не залежить від кількості вхідних у систему точок і тіл. Наприклад, машини й механізми складаються з багатьох тіл (деталей), а мають звичайно одну-дві ступені свободи; отже, вивчення їхнього руху потребує складання лише одного-двох рівнянь Лагранжа (тому вони широко використовуються в динаміці машин і механізмів, у теорії коливань, теорії гіроскопа і т.д.).
, які однозначно визначають положення системи в просторі (причому число невідомих дорівнює числу рівнянь). Велика перевага рівнянь Лагранжа полягає в тому, що їхнє число дорівнює числу ступенів свободи системи й не залежить від кількості вхідних у систему точок і тіл. Наприклад, машини й механізми складаються з багатьох тіл (деталей), а мають звичайно одну-дві ступені свободи; отже, вивчення їхнього руху потребує складання лише одного-двох рівнянь Лагранжа (тому вони широко використовуються в динаміці машин і механізмів, у теорії коливань, теорії гіроскопа і т.д.).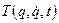 й за допомогою (13.10) по заданим силам
й за допомогою (13.10) по заданим силам 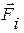 визначаються узагальнені сили
визначаються узагальнені сили  , т. ч. будуть звичайними диференціальними рівняннями другого порядку відносно невідомих
, т. ч. будуть звичайними диференціальними рівняннями другого порядку відносно невідомих 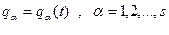 , тобто закон руху системи в узагальнених координатах (при необхідності за допомогою (13.13) знаходять потім координатну форму закону руху системи
, тобто закон руху системи в узагальнених координатах (при необхідності за допомогою (13.13) знаходять потім координатну форму закону руху системи  ).
). - два набори узагальнених координат однієї й тієї ж системи, то ці набори є однозначні функції один одного вигляду:
- два набори узагальнених координат однієї й тієї ж системи, то ці набори є однозначні функції один одного вигляду: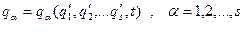 (13.14)
(13.14)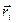 через
через  :
:
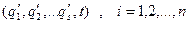 (13.15)
(13.15)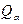 і кінетичною енергією Т. Розглянемо спочатку залежність форми (13.13) від вигляду функцій
і кінетичною енергією Т. Розглянемо спочатку залежність форми (13.13) від вигляду функцій  .
.
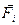 (як внутрішні так і зовнішні) є потенціальними, тобто
(як внутрішні так і зовнішні) є потенціальними, тобто 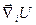 , де
, де  - повна потенціальна енергія системи (див. § 7). Підставляючи сюди (13.3), тобто розглядаючи U як неявну функцію узагальненої сили (13.10), маємо:
- повна потенціальна енергія системи (див. § 7). Підставляючи сюди (13.3), тобто розглядаючи U як неявну функцію узагальненої сили (13.10), маємо: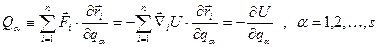 , (13.16)
, (13.16)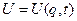 , а залежність
, а залежність 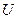 від
від 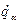 , тобто
, тобто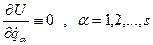 . (13.17)
. (13.17)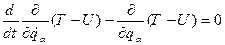 ,
,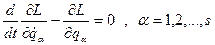 , (13.18)
, (13.18) (13.19)
(13.19)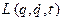 є найважливішою функцією стану механічної системи.
є найважливішою функцією стану механічної системи.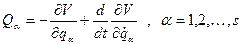 , (13.20)
, (13.20)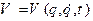 - так званий узагальнений потенціал, або потенціал, що залежить від швидкості. Функція Лагранжа для зазначених систем визначається як різниця кінетичної енергії системи і її узагальненого потенціалу, тобто:
- так званий узагальнений потенціал, або потенціал, що залежить від швидкості. Функція Лагранжа для зазначених систем визначається як різниця кінетичної енергії системи і її узагальненого потенціалу, тобто: . (13.21)
. (13.21) , (13.22)
, (13.22) (або
(або  )
) , (13.23)
, (13.23)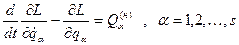 , (13.24)
, (13.24) (або
(або  ).
). невільної системи і її вплив на вигляд
невільної системи і її вплив на вигляд 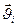 матеріальних точок системи. Однак кінетична енергія невільної системи в загальному випадку виявляється неоднорідною квадратичною формою відносно узагальнених швидкостей
матеріальних точок системи. Однак кінетична енергія невільної системи в загальному випадку виявляється неоднорідною квадратичною формою відносно узагальнених швидкостей  кінетичної енергії, одержуємо:
кінетичної енергії, одержуємо: , (13.25)
, (13.25) ,
, 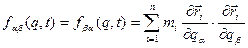 , (13.26)
, (13.26) ,
, 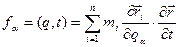 , (13.27)
, (13.27)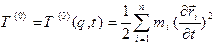 . (13.28)
. (13.28) виявляється неоднорідною квадратичною формою
виявляється неоднорідною квадратичною формою  ; 2) як
; 2) як 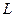 системи стають явно залежними від часу.
системи стають явно залежними від часу.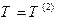 ,
,  і функцію Лагранжа системи можна представити у вигляді (див. (13.19) і (13.26)):
і функцію Лагранжа системи можна представити у вигляді (див. (13.19) і (13.26)): . (13.29)
. (13.29) - однорідна функція порядку n, то має місце рівність (теорема Ейлера)
- однорідна функція порядку n, то має місце рівність (теорема Ейлера) . (13.30)
. (13.30)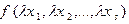 =
= 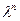
 , маємо:
, маємо: .
. маємо наступну рівність:
маємо наступну рівність: , (13.32)
, (13.32)


