Алгоритм вычисления собственных векторов линейного оператора1) Зафиксировать произвольный базис 2) Составить и решить (в множестве действительных или комплексных чисел) характеристическое уравнение (5.5). Его корни 3) При каждом найденном собственном значении Пример 5.2. Задана матрица
некоторого линейного оператора в базисе Решение. Матрица линейного оператора в базисе
Его корни (собственные значения линейного оператора):
Алгебраическая кратность
Соответствующая однородная система (5.4) имеет вид
Полагая в системе (5.7)
общее решение которой имеет вид
Найдем соответствующую фундаментальную систему решений
Вектор-столбцы Аналогично положив в системе (5.7)
|

 линейного пространства и найти матрицу
линейного пространства и найти матрицу 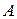 линейного оператора в этом базисе;
линейного оператора в этом базисе;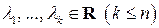 и есть собственные значения линейного оператора;
и есть собственные значения линейного оператора;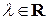 однородная система (5.4) будет иметь ненулевые решения. Выделив фундаментальную систему линейно независимых решений, получим либо единственный собственный вектор
однородная система (5.4) будет иметь ненулевые решения. Выделив фундаментальную систему линейно независимых решений, получим либо единственный собственный вектор 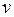 , либо систему r линейно независимых собственных векторов
, либо систему r линейно независимых собственных векторов 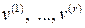 линейного оператора, соответствующих собственному значению
линейного оператора, соответствующих собственному значению 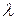 .
.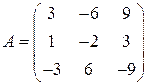
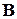 пространства
пространства  . Найти собственные значения и соответствующие собственные векторы линейного оператора.
. Найти собственные значения и соответствующие собственные векторы линейного оператора.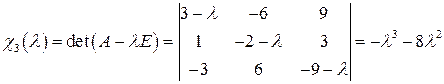 .
.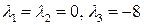 , записанные с учетом алгебраических кратностей. Алгебраическая кратность
, записанные с учетом алгебраических кратностей. Алгебраическая кратность 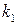 собственного числа
собственного числа  равна двум, так как
равна двум, так как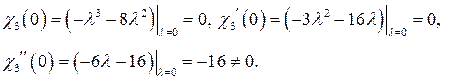
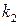 собственного числа
собственного числа  равна единице, так как
равна единице, так как .
. (5.7)
(5.7)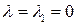 , получим однородную систему
, получим однородную систему

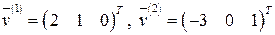 .
.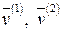 есть координатные вектор-столбцы собственных векторов
есть координатные вектор-столбцы собственных векторов  , отвечающих собственному числу
, отвечающих собственному числу  собственного вектора
собственного вектора 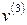 .
.


