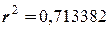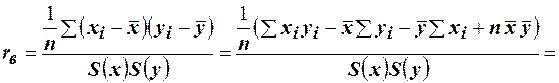
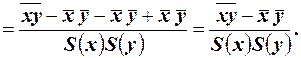
Пример 50. Вычислить выборочный коэффициент корреляции по следующим данным:
Решение. Вычислим 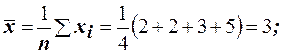
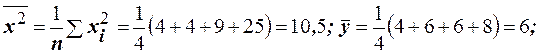
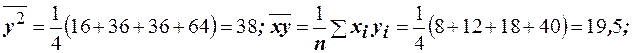
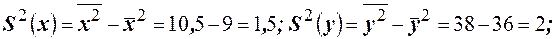
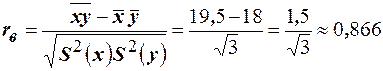 .
.
56. Метод вычисления выборочного коэффициента
корреляции для вариационных рядов
Для вычисления выборочного коэффициента корреляции строят корреляционную таблицу. Для этого разбиваем каждый вариационный ряд на интервальный. Затем находятся входящие в формулу для вычисления выборочного коэффициента корреляции параметры.
Пример 51. По данным наблюдений над случайными величинами X и Y получена выборка, приведённая в таблице
| №
| X
| Y
| №
| X
| Y
| №
| X
| Y
| №
| X
| Y
|
|
| 7,1
| 10,0
|
| 14,8
| 35,3
|
| 10,9
| 18,2
|
| 16,1
| 30,1
|
|
| 9,5
| 6,7
|
| 17,2
| 36,3
|
| 11,4
| 18,7
|
| 18,2
| 27,2
|
|
| 11,0
| 14,0
|
| 19,2
| 37,4
|
| 12,3
| 17,6
|
| 19,1
| 30,9
|
|
| 12,3
| 15,1
|
| 22,3
| 38,0
|
| 13,2
| 18,1
|
| 17,9
| 35,1
|
|
| 11,8
| 24,2
|
| 17,2
| 40,2
|
| 13,1
| 24,1
|
| 18,7
| 36,1
|
|
| 14,1
| 19,9
|
| 19,9
| 42,4
|
| 13,6
| 21,3
|
| 12,4
| 17,6
|
|
| 15,1
| 24,3
|
| 20,1
| 44,5
|
| 13,7
| 19,8
|
| 12,5
| 18,6
|
|
| 14,7
| 22,2
|
| 21,7
| 42,4
|
| 14,6
| 24,1
|
| 12,7
| 19,2
|
|
| 16,1
| 21,0
|
| 8,5
| 12,2
|
| 14,2
| 21,3
|
| 14,1
| 26,2
|
|
| 13,1
| 30,1
|
| 9,7
| 12,4
|
| 15,2
| 25,2
|
| 14,6
| 27,4
|
|
| 13,8
| 28,1
|
| 10,2
| 12,5
|
| 16,1
| 21,1
|
| 14,9
| 30,1
|
|
| 16,9
| 30,3
|
| 11,1
| 12,9
|
| 17,2
| 24,6
|
|
|
|
|
| 19,1
| 27,3
|
| 11,3
| 16,1
|
| 18,0
| 23,3
|
|
|
|
Найдём оптимальные длины интервалов и количество интервалов, используя формулу Стэрджеса. Для переменной Х наименьшее значение - 7,1 наибольшее - 22,3, тогда оптимальное число интервалов равно 7 с шагом, равным 2,2, при этом получаем такие интервалы: 
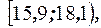
 . Для переменной У минимальное значение - 6,7 наибольшее - 44,5, тогда оптимальное число интервалов 6 с шагом, равным 6,3. Получаем интервалы
. Для переменной У минимальное значение - 6,7 наибольшее - 44,5, тогда оптимальное число интервалов 6 с шагом, равным 6,3. Получаем интервалы 
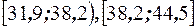 . Распределим наблюдения по полученным интервалам получим корреляционную таблицу. В таблицу вместо интервалов запишем их середины
. Распределим наблюдения по полученным интервалам получим корреляционную таблицу. В таблицу вместо интервалов запишем их середины
| У
| Х
| 
|
| 8,2
| 10,4
| 12,6
| 14,8
| 17,0
| 19,2
| 21,4
|
| 9,85
|
|
|
|
|
|
|
|
|
| 16,15
|
|
|
|
|
|
|
|
|
| 22,45
|
|
|
|
|
|
|
|
|
| 28,75
|
|
|
|
|
|
|
|
|
| 35,05
|
|
|
|
|
|
|
|
|
| 41,35
|
|
|
|
|
|
|
|
|
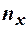
|
|
|
|
|
|
|
|
|
Для упрощения расчётов перейдём к условным вариантам 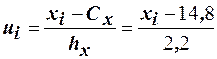 и
и 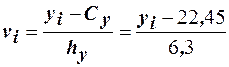 . Составим расчётную таблицу.
. Составим расчётную таблицу.
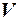
| 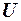
| 
| 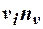
| 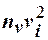
|
| -3
| -2
| -1
|
|
|
|
|
| -2
|
|
|
|
|
|
|
|
| -12
|
|
| -1
|
|
|
|
|
|
|
|
| -10
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
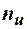
|
|
|
|
|
|
|
|
|
|
|
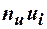
| -6
| -16
| -10
|
|
|
|
| -2
|

|
|
|
|
|
|
|
|
|
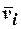
| -2
| -1,5
| -0,5
| 0,5
|
| 
| 
|
|
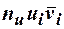
|
|
|
|
|
|
|
|
|
Для вычисления выборочного коэффициента корреляции используем формулу 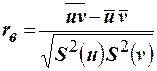 , где
, где 



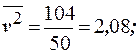
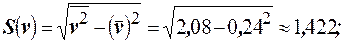

 .
.
57. Проверка гипотезы о значимости
коэффициента корреляции
На практике коэффициент корреляции r обычно неизвестен. По результатам выборки может быть найдена его точечная оценка – выборочный коэффициент корреляции  . Равенство нулю выборочного коэффициента корреляции ещё не свидетельствует о равенстве нулю самого коэффициента корреляции, а следовательно, о некоррелированности случайных величин Х и У. Чтобы выяснить, находятся ли случайные величины в корреляционной зависимости, нужно проверить значимость выборочного коэффициента корреляции
. Равенство нулю выборочного коэффициента корреляции ещё не свидетельствует о равенстве нулю самого коэффициента корреляции, а следовательно, о некоррелированности случайных величин Х и У. Чтобы выяснить, находятся ли случайные величины в корреляционной зависимости, нужно проверить значимость выборочного коэффициента корреляции  , то есть установить, достаточна ли его величина для обоснованного вывода о наличии корреляционной связи. Для этого проверяют нулевую гипотезу
, то есть установить, достаточна ли его величина для обоснованного вывода о наличии корреляционной связи. Для этого проверяют нулевую гипотезу 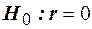 . Предполагается наличие двухмерного нормального распределения случайных переменных; объём выборки может быть любым. Вычисляют статистику
. Предполагается наличие двухмерного нормального распределения случайных переменных; объём выборки может быть любым. Вычисляют статистику  , которая имеет распределение Стьюдента с
, которая имеет распределение Стьюдента с  степенями свободы. Для проверки нулевой гипотезы по уровню значимости
степенями свободы. Для проверки нулевой гипотезы по уровню значимости 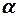 и числу степеней свободы
и числу степеней свободы 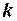 находят по таблице распределения Стьюдента критическое значение
находят по таблице распределения Стьюдента критическое значение 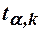 . Если
. Если  , то нулевую гипотезу об отсутствии корреляционной связи между переменными Х и У следует отвергнуть. Переменные считают зависимыми. При
, то нулевую гипотезу об отсутствии корреляционной связи между переменными Х и У следует отвергнуть. Переменные считают зависимыми. При 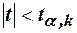 , нет оснований отвергнуть нулевую гипотезу.
, нет оснований отвергнуть нулевую гипотезу.
В случае значимого выборочного коэффициента корреляции есть смысл построить доверительный интервал для коэффициента корреляции 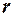 . Однако для этого нужно знать закон распределения выборочного коэффициента корреляции
. Однако для этого нужно знать закон распределения выборочного коэффициента корреляции  . Плотность вероятности выборочного коэффициента корреляции имеет сложный вид, поэтому прибегают к специально подобранным функциям от выборочного коэффициента корреляции, которые сводятся к хорошо изученным распределениям, например к нормальному или Стьюдента. Чаще всего для подбора функции применяют преобразование Фишера. Вычисляют статистику
. Плотность вероятности выборочного коэффициента корреляции имеет сложный вид, поэтому прибегают к специально подобранным функциям от выборочного коэффициента корреляции, которые сводятся к хорошо изученным распределениям, например к нормальному или Стьюдента. Чаще всего для подбора функции применяют преобразование Фишера. Вычисляют статистику 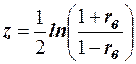 , где
, где  - гиперболический тангенс от
- гиперболический тангенс от  . Распределение статистики
. Распределение статистики  хорошо аппроксимируется нормальным распределением с параметрами
хорошо аппроксимируется нормальным распределением с параметрами  . В этом случае доверительный интервал для
. В этом случае доверительный интервал для 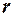 имеет вид
имеет вид  . Величины
. Величины 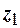 и
и 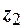 находятся по формулам
находятся по формулам 
 , где
, где  .
.
Пример 52. Проверить значимость выборочного коэффициента корреляции из примера 51 и найти доверительный интервал с надёжностью 0,95 для него.
Решение. Для проверки значимости найдём статистику 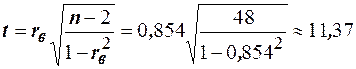 . По уровню значимости
. По уровню значимости 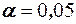 и числу степеней свободы
и числу степеней свободы  найдём
найдём  (см. приложение табл.3). Так как
(см. приложение табл.3). Так как  , то нулевую гипотезу об отсутствии корреляционной связи между переменными Х и У следует отвергнуть. Следовательно, выборочный коэффициент корреляции значим. Найдём доверительный интервал для выборочного коэффициента корреляции, вычислим
, то нулевую гипотезу об отсутствии корреляционной связи между переменными Х и У следует отвергнуть. Следовательно, выборочный коэффициент корреляции значим. Найдём доверительный интервал для выборочного коэффициента корреляции, вычислим  ,
,  , тогда
, тогда 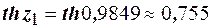 и
и  . Следовательно, доверительный интервал для выборочного коэффициента корреляции имеет вид
. Следовательно, доверительный интервал для выборочного коэффициента корреляции имеет вид 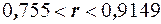 .
.
58. Эмпирическая и теоретическая
линии регрессии
Определить форму связи – значит выявить механизм получения зависимой случайной величины.
Кривой регрессии У по Х (или Х по У) называют условное среднее значение случайной величины У, рассматриваемое как функция определённого класса, параметры которой находятся методом наименьших квадратов по наблюдённым значениям двухмерной случайной величины. То есть уравнение линейной регрессии имеет вид 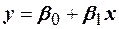 . Оценке в этом случае подлежат параметры
. Оценке в этом случае подлежат параметры 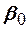 и
и 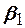 , называемые коэффициентами регрессии, а также
, называемые коэффициентами регрессии, а также  - остаточная дисперсия. Остаточной дисперсией называется та часть рассеивания результативного признака, которую нельзя объяснить действием наблюдаемого признака.
- остаточная дисперсия. Остаточной дисперсией называется та часть рассеивания результативного признака, которую нельзя объяснить действием наблюдаемого признака.
Пример 53. Построить эмпирическую и теоретическую линии регрессии по данным примера 51.
Решение. Уравнение теоретической линии регрессии имеет вид 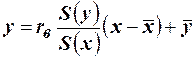 ,
,
где: 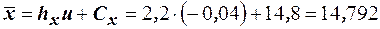 ,
,
 ,
,  ,
,  . Тогда уравнение регрессии имеет вид
. Тогда уравнение регрессии имеет вид 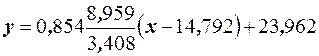 или
или 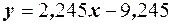 . Для построения возьмём точки
. Для построения возьмём точки 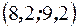 и
и 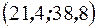 . При построении эмпирической линии регрессии используем точки вида
. При построении эмпирической линии регрессии используем точки вида  , где значения
, где значения  находятся по формуле
находятся по формуле 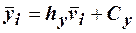 . Получаем
. Получаем  ,
,
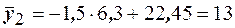 ,
, 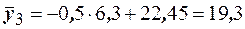 ,
,
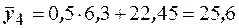 ,
, 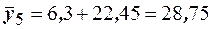 ,
,
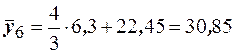 ,
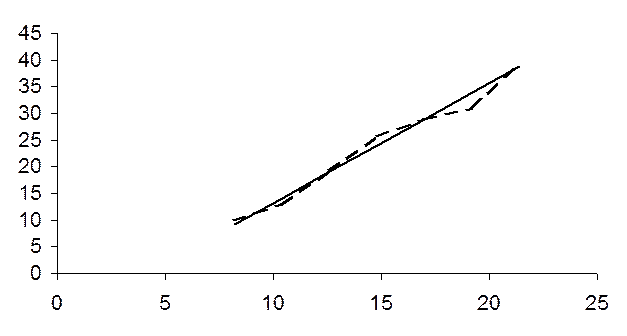
,  . Построим на плоскости точки с координатами
. Построим на плоскости точки с координатами 
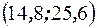 ,
, 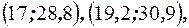
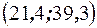 и, соединив их в порядке возрастания х, получим эмпирическую линию регрессии.
и, соединив их в порядке возрастания х, получим эмпирическую линию регрессии.
 Значимость коэффициентов регрессии
Значимость коэффициентов регрессии
Проверить значимость оценок коэффициентов регрессии – значит установить, достаточна ли величина оценки для статистически обоснованного вывода о том, что коэффициенты регрессии отличны от нуля. Для этого проверяют гипотезу о равенстве нулю коэффициентов регрессии, соблюдая предпосылки нормальной регрессии.
Для заданной выборки методом наименьших квадратов находим уравнение линии регрессии
Вычисляем статистику 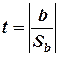 , которая имеет
, которая имеет  степеней свободы, b – оценка коэффициента регрессии,
степеней свободы, b – оценка коэффициента регрессии,  - оценка среднего квадратического отклонения коэффициента, иначе стандартная ошибка оценки. По уровню значимости и числу степеней свободы по таблице находят
- оценка среднего квадратического отклонения коэффициента, иначе стандартная ошибка оценки. По уровню значимости и числу степеней свободы по таблице находят  . Если
. Если  , то гипотезу о равенстве нулю коэффициента регрессии отвергают, следовательно, при заданном уровне значимости коэффициент регрессии значим. Оценки среднего квадратического отклонения находятся по формулам
, то гипотезу о равенстве нулю коэффициента регрессии отвергают, следовательно, при заданном уровне значимости коэффициент регрессии значим. Оценки среднего квадратического отклонения находятся по формулам  ,
, 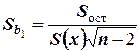 , где
, где  и
и 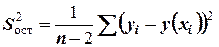 .
.
Доверительные интервалы для коэффициентов регрессии находятся по формулам  .
.
Пример 54. Проверить значимость коэффициентов регрессии и найти доверительные интервалы для них при уровне значимости 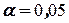 по данным предыдущей задачи.
по данным предыдущей задачи.
Решение. Уравнение регрессии имеет вид  . Найдём остаточную дисперсию
. Найдём остаточную дисперсию 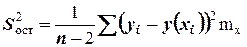 , для этого составим таблицу:
, для этого составим таблицу:

| 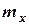
| 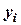
| 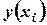
| 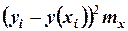
|
| 8,2
|
| 9,85
| 9,164
| 0,941192
|
| 10,4
|
|
| 14,1
| 9,732872
|
| 12,6
|
| 19,3
| 19,04
| 0,66564
|
| 14,8
|
| 25,6
| 23,98
| 31,453932
|
| 17,0
|
| 28,8
| 28,92
| 0,1296
|
| 19,2
|
| 30,9
| 33,86
| 52,534086
|
| 21,4
|
| 39,3
| 38,8
| 0,756012
|
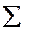
|
|
|
| 96,213334
|
Следовательно, остаточная дисперсия равна 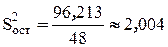 тогда
тогда  ,
,  ,
,  ,
, 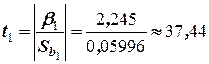 . По таблице (см. приложение табл. 5) находим
. По таблице (см. приложение табл. 5) находим  . Так как
. Так как  и
и  , то оба коэффициента значимы. Доверительный интервал для
, то оба коэффициента значимы. Доверительный интервал для 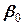 имеет вид
имеет вид
 или
или  . Доверительный интервал для
. Доверительный интервал для  имеет вид
имеет вид  или
или 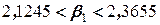 .
.
Пример 55. Найти коэффициенты уравнения  регрессии, проверить их значимость и построить доверительные интервалы при уровне значимости
регрессии, проверить их значимость и построить доверительные интервалы при уровне значимости 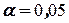 по данной выборке
по данной выборке
Решение. Найдём коэффициенты регрессии по формулам 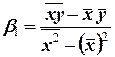 и
и  . Вычислим значения входящих в формулы величин:
. Вычислим значения входящих в формулы величин:
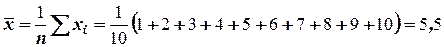 ,
,
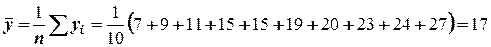 ,
, 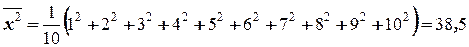 ,
,
 ,
,
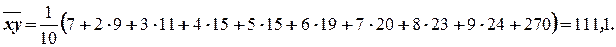
Тогда  и
и  , следовательно, уравнение регрессии имеет вид
, следовательно, уравнение регрессии имеет вид  . Проверим значимость коэффициентов регрессии. Для этого вычислим
. Проверим значимость коэффициентов регрессии. Для этого вычислим 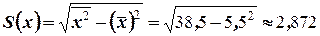 . Найдём
. Найдём 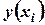 , используя уравнение регрессии
, используя уравнение регрессии
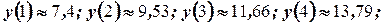
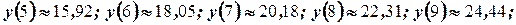
 . Найдём остаточную дисперсию по формуле
. Найдём остаточную дисперсию по формуле 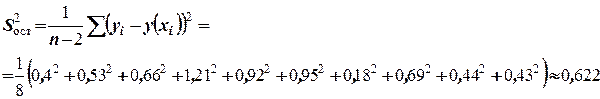
Вычислим 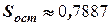 , тогда
, тогда  и
и 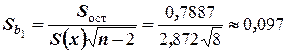 . Статистики равны
. Статистики равны  и
и 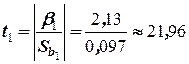 . По таблице (см. приложение табл. 5) находим
. По таблице (см. приложение табл. 5) находим  . Так как
. Так как  и
и  , то оба коэффициента значимы. Доверительный интервал для
, то оба коэффициента значимы. Доверительный интервал для 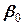 имеет вид
имеет вид
 или
или  . Доверительный интервал для
. Доверительный интервал для  имеет вид
имеет вид  или
или  .
.
60. Корреляционное отношение
На практике часто предпосылки корреляционного анализа нарушаются: один из признаков оказывается неслучайным, или признаки не имеют нормального распределения. Для изучения связи между ними в этом случае существует показатель зависимости признаков, основанный на показателе изменчивости общей (или полной) дисперсии.
Полной называется дисперсия признака относительно его математического ожидания. Так для признака У это  . Дисперсию
. Дисперсию 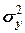 можно разложить на две составляющие, одна из которых характеризует влияние фактора Х на У, другая - влияние прочих факторов. Очевидно, чем меньше влияние прочих факторов, тем теснее связь, тем более приближается она к функциональной.
можно разложить на две составляющие, одна из которых характеризует влияние фактора Х на У, другая - влияние прочих факторов. Очевидно, чем меньше влияние прочих факторов, тем теснее связь, тем более приближается она к функциональной.
По выборочным данным рассчитываем выборочное корреляционное отношение  , где
, где  и
и 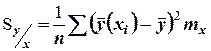 . Значения
. Значения 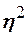 лежащие в интервале
лежащие в интервале  , являются показателями тесноты группировки точек около кривой регрессии независимо от её вида (формы связи). Если зависимость является линейной то корреляционное отношение совпадает с коэффициентом корреляции:
, являются показателями тесноты группировки точек около кривой регрессии независимо от её вида (формы связи). Если зависимость является линейной то корреляционное отношение совпадает с коэффициентом корреляции:  .
.
Если зависимость является нелинейной то  .
.
Пример 56. Вычислить корреляционное отношение по выборке
Предполагая что, зависимость между переменными имеет вид: 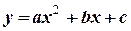 .
.
Решение. Согласно методу наименьших квадратов для определения коэффициентов имеем систему уравнений
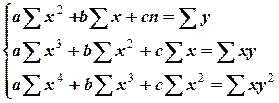
Составим расчетную таблицу для расчётов параметров зависимости
Получаем систему уравнений
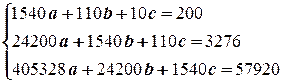
Следовательно, зависимость имеет вид 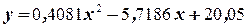 . Найдём значение корреляционного отношения, для этого составим таблицу
. Найдём значение корреляционного отношения, для этого составим таблицу
| №
| 
| 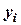
| 
| 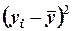
| 
|
|
|
|
| 10,24546
|
| 95,15113
|
|
|
|
| 3,706064
|
| 265,4924
|
|
|
|
| 0,431824
|
| 382,9135
|
|
|
|
| 0,422736
|
| 383,2693
|
|
|
|
| 3,6788
|
| 266,3816
|
|
|
|
| 10,20002
|
| 96,03969
|
|
|
|
| 19,98638
|
| 0,000185
|
|
|
|
| 33,0379
|
| 169,9869
|
|
|
|
| 49,35458
|
| 861,6911
|
|
|
|
| 68,9364
|
| 2394,771
|
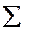
|
|
| 200,0002
|
| 4915,697
|
Тогда корреляционное отношение равно  .
.
Коэффициент корреляции равен  и
и 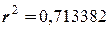

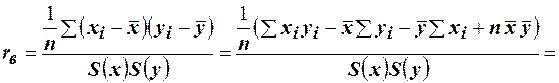
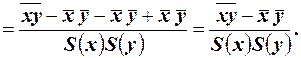
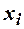
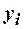
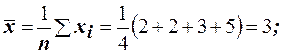
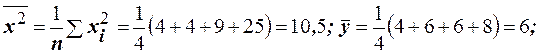
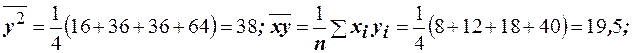
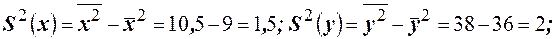
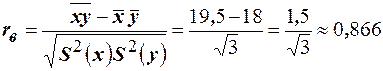 .
.
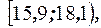
 . Для переменной У минимальное значение - 6,7 наибольшее - 44,5, тогда оптимальное число интервалов 6 с шагом, равным 6,3. Получаем интервалы
. Для переменной У минимальное значение - 6,7 наибольшее - 44,5, тогда оптимальное число интервалов 6 с шагом, равным 6,3. Получаем интервалы 
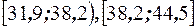 . Распределим наблюдения по полученным интервалам получим корреляционную таблицу. В таблицу вместо интервалов запишем их середины
. Распределим наблюдения по полученным интервалам получим корреляционную таблицу. В таблицу вместо интервалов запишем их середины
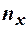
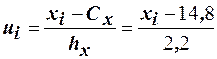 и
и 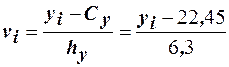 . Составим расчётную таблицу.
. Составим расчётную таблицу.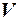
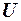

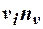
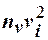
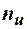
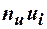

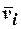


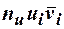
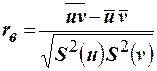 , где
, где 



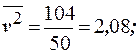
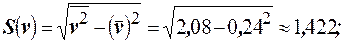

 .
. . Равенство нулю выборочного коэффициента корреляции ещё не свидетельствует о равенстве нулю самого коэффициента корреляции, а следовательно, о некоррелированности случайных величин Х и У. Чтобы выяснить, находятся ли случайные величины в корреляционной зависимости, нужно проверить значимость выборочного коэффициента корреляции
. Равенство нулю выборочного коэффициента корреляции ещё не свидетельствует о равенстве нулю самого коэффициента корреляции, а следовательно, о некоррелированности случайных величин Х и У. Чтобы выяснить, находятся ли случайные величины в корреляционной зависимости, нужно проверить значимость выборочного коэффициента корреляции 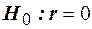 . Предполагается наличие двухмерного нормального распределения случайных переменных; объём выборки может быть любым. Вычисляют статистику
. Предполагается наличие двухмерного нормального распределения случайных переменных; объём выборки может быть любым. Вычисляют статистику  , которая имеет распределение Стьюдента с
, которая имеет распределение Стьюдента с  степенями свободы. Для проверки нулевой гипотезы по уровню значимости
степенями свободы. Для проверки нулевой гипотезы по уровню значимости 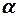 и числу степеней свободы
и числу степеней свободы 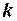 находят по таблице распределения Стьюдента критическое значение
находят по таблице распределения Стьюдента критическое значение 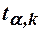 . Если
. Если  , то нулевую гипотезу об отсутствии корреляционной связи между переменными Х и У следует отвергнуть. Переменные считают зависимыми. При
, то нулевую гипотезу об отсутствии корреляционной связи между переменными Х и У следует отвергнуть. Переменные считают зависимыми. При 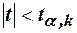 , нет оснований отвергнуть нулевую гипотезу.
, нет оснований отвергнуть нулевую гипотезу.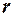 . Однако для этого нужно знать закон распределения выборочного коэффициента корреляции
. Однако для этого нужно знать закон распределения выборочного коэффициента корреляции 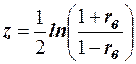 , где
, где  - гиперболический тангенс от
- гиперболический тангенс от  . Распределение статистики
. Распределение статистики  . В этом случае доверительный интервал для
. В этом случае доверительный интервал для  . Величины
. Величины 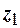 и
и 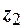 находятся по формулам
находятся по формулам 
 , где
, где  .
.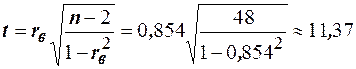 . По уровню значимости
. По уровню значимости 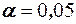 и числу степеней свободы
и числу степеней свободы  найдём
найдём  (см. приложение табл.3). Так как
(см. приложение табл.3). Так как  ,
,  , тогда
, тогда 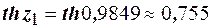 и
и  . Следовательно, доверительный интервал для выборочного коэффициента корреляции имеет вид
. Следовательно, доверительный интервал для выборочного коэффициента корреляции имеет вид 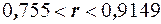 .
.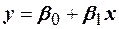 . Оценке в этом случае подлежат параметры
. Оценке в этом случае подлежат параметры 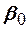 и
и 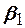 , называемые коэффициентами регрессии, а также
, называемые коэффициентами регрессии, а также  - остаточная дисперсия. Остаточной дисперсией называется та часть рассеивания результативного признака, которую нельзя объяснить действием наблюдаемого признака.
- остаточная дисперсия. Остаточной дисперсией называется та часть рассеивания результативного признака, которую нельзя объяснить действием наблюдаемого признака.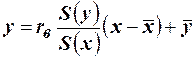 ,
,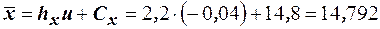 ,
, ,
,  ,
,  . Тогда уравнение регрессии имеет вид
. Тогда уравнение регрессии имеет вид 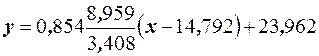 или
или 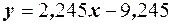 . Для построения возьмём точки
. Для построения возьмём точки 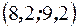 и
и 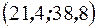 . При построении эмпирической линии регрессии используем точки вида
. При построении эмпирической линии регрессии используем точки вида  , где значения
, где значения  находятся по формуле
находятся по формуле 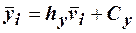 . Получаем
. Получаем  ,
,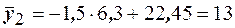 ,
, 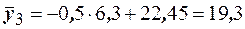 ,
,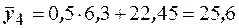 ,
, 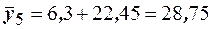 ,
,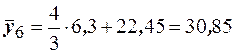 ,
,  . Построим на плоскости точки с координатами
. Построим на плоскости точки с координатами 
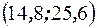 ,
, 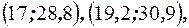
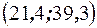 и, соединив их в порядке возрастания х, получим эмпирическую линию регрессии.
и, соединив их в порядке возрастания х, получим эмпирическую линию регрессии. Значимость коэффициентов регрессии
Значимость коэффициентов регрессии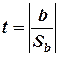 , которая имеет
, которая имеет  степеней свободы, b – оценка коэффициента регрессии,
степеней свободы, b – оценка коэффициента регрессии,  - оценка среднего квадратического отклонения коэффициента, иначе стандартная ошибка оценки. По уровню значимости и числу степеней свободы по таблице находят
- оценка среднего квадратического отклонения коэффициента, иначе стандартная ошибка оценки. По уровню значимости и числу степеней свободы по таблице находят  . Если
. Если  , то гипотезу о равенстве нулю коэффициента регрессии отвергают, следовательно, при заданном уровне значимости коэффициент регрессии значим. Оценки среднего квадратического отклонения находятся по формулам
, то гипотезу о равенстве нулю коэффициента регрессии отвергают, следовательно, при заданном уровне значимости коэффициент регрессии значим. Оценки среднего квадратического отклонения находятся по формулам  ,
, 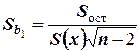 , где
, где  и
и 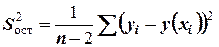 .
. .
.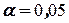 по данным предыдущей задачи.
по данным предыдущей задачи. . Найдём остаточную дисперсию
. Найдём остаточную дисперсию 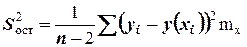 , для этого составим таблицу:
, для этого составим таблицу:
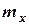
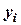
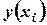
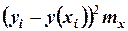
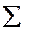
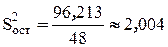 тогда
тогда  ,
,  ,
,  ,
, 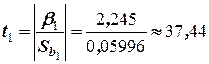 . По таблице (см. приложение табл. 5) находим
. По таблице (см. приложение табл. 5) находим  . Так как
. Так как  и
и  , то оба коэффициента значимы. Доверительный интервал для
, то оба коэффициента значимы. Доверительный интервал для 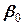 имеет вид
имеет вид или
или  . Доверительный интервал для
. Доверительный интервал для  имеет вид
имеет вид  или
или 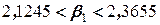 .
. регрессии, проверить их значимость и построить доверительные интервалы при уровне значимости
регрессии, проверить их значимость и построить доверительные интервалы при уровне значимости 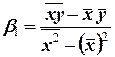 и
и  . Вычислим значения входящих в формулы величин:
. Вычислим значения входящих в формулы величин: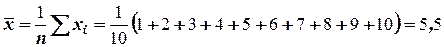 ,
,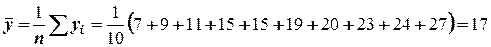 ,
, 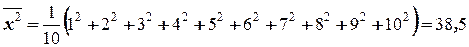 ,
, ,
,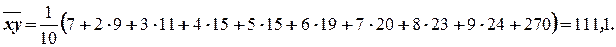
 и
и  , следовательно, уравнение регрессии имеет вид
, следовательно, уравнение регрессии имеет вид  . Проверим значимость коэффициентов регрессии. Для этого вычислим
. Проверим значимость коэффициентов регрессии. Для этого вычислим 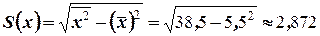 . Найдём
. Найдём 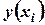 , используя уравнение регрессии
, используя уравнение регрессии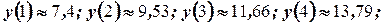
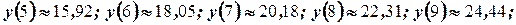
 . Найдём остаточную дисперсию по формуле
. Найдём остаточную дисперсию по формуле 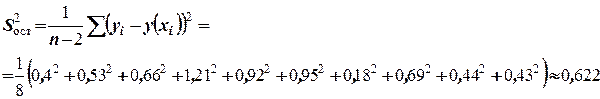
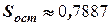 , тогда
, тогда  и
и 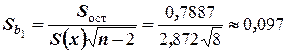 . Статистики равны
. Статистики равны  и
и 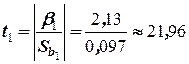 . По таблице (см. приложение табл. 5) находим
. По таблице (см. приложение табл. 5) находим  . Так как
. Так как  или
или  . Доверительный интервал для
. Доверительный интервал для  или
или  .
. . Дисперсию
. Дисперсию 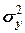 можно разложить на две составляющие, одна из которых характеризует влияние фактора Х на У, другая - влияние прочих факторов. Очевидно, чем меньше влияние прочих факторов, тем теснее связь, тем более приближается она к функциональной.
можно разложить на две составляющие, одна из которых характеризует влияние фактора Х на У, другая - влияние прочих факторов. Очевидно, чем меньше влияние прочих факторов, тем теснее связь, тем более приближается она к функциональной. , где
, где  и
и 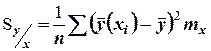 . Значения
. Значения 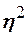 лежащие в интервале
лежащие в интервале  , являются показателями тесноты группировки точек около кривой регрессии независимо от её вида (формы связи). Если зависимость является линейной то корреляционное отношение совпадает с коэффициентом корреляции:
, являются показателями тесноты группировки точек около кривой регрессии независимо от её вида (формы связи). Если зависимость является линейной то корреляционное отношение совпадает с коэффициентом корреляции:  .
. .
.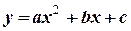 .
.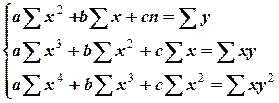


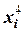


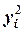
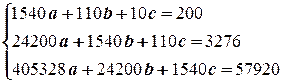
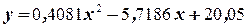 . Найдём значение корреляционного отношения, для этого составим таблицу
. Найдём значение корреляционного отношения, для этого составим таблицу
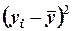

 .
. и
и