3 страница. ☺ Формула следует непосредственно из формулы
☺ Формула следует непосредственно из формулы 17. Непрерывная случайная величина (НОВ). Вероятность отдельно взятого значения НСВ. Математическое ожидание и дисперсия нсв.
Теорема. Вероятность любого отдельно взятого значения непрерывной случайной величины равна нулю. ☺ Покажем, что для любого значения Применяя свойство
Из приведенной выше теоремы следует, что нулевой вероятностью могут обладать и возможные события, так как событие, состоящее в том, что случайная величина Х приняла конкретное значение Следствие. Если Х - непрерывная случайная величина, то вероятность попадания случайной величины в интервал
Математическим ожиданием непрерывной случайной величины Х, возможные значения которой принадлежат отрезку [a,b], называется определенный интеграл Дисперсией непрерывной случайной величины называется математическое ожидание квадрата ее отклонения. По аналогии с дисперсией дискретной случайной величины, для практического вычисления дисперсии используется формула: 18. Плотность вероятности непрерывной случайной величины, ее определение, свойства и график.
Про случайную величину Х говорят, что она имеет распределение (распределена) с плотностью Свойства плотности вероятности непрерывной случайной величины. 1. Плотность вероятности - неотрицательная функция, т.е. ☺ 2. Вероятность попадания непрерывной случайной величины в интервал [а,b] равна определенному интегралу от ее плотности вероятности в пределах от а до b, т.е.
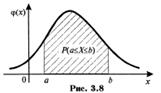
Геометрически полученная вероятность равна площади фигуры, ограниченной сверху кривой распределения и опирающейся на отрезок [а,b] (рис. 3.8).
3. Функция распределения непрерывной случайной величины может быть выражена через плотность вероятности по формуле:
Геометрически функция распределения равна площади фигуры, ограниченной сверху кривой распределения и лежащей левее точки х (рис. 3.9). 4. Несобственный интеграл в бесконечных пределах от плотности вероятности непрерывной случайной величины равен единице: Геометрически свойства 1 и 4 плотности вероятности означают, что ее график - кривая распределения - лежит не ниже оси абсцисс, и полная площадь фигуры, ограниченной кривой распределения и осью абсцисс, равна единице. 19. Случайная величина, распределенная по биномиальному закону, ее математическое ожидание и дисперсия. Закон распределения Пуассона. Определение. Дискретная случайная величина Х имеет биномиальный закон распределения с параметрами npq, если она принимает значения 0, 1, 2,..., m,...,n с вероятностями
где 0<р<l, q=1-p. Как видим, вероятности Р(Х=m) находятся по формуле Бернулли, следовательно, биномиальный закон распределения представляет собой закон распределения числа Х=m наступлений события А в n независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью р. Ряд распределения биномиального закона имеет вид:
Очевидно, что определение биномиального закона корректно, т.к. основное свойство ряда распределения Математическое ожидание случайной величины Х, распределенной по биноминальному закону,
Определение. Дискретная случайная величина Х имеет закон распределения Пуассона с параметром λ > 0, если она принимает значения 0, 1, 2,..., m,... (бесконечное, но счетное множество значений) с вероятностями Ряд распределения закона Пуассона имеет вид:
Очевидно, что определение закона Пуассона корректно, так как основное свойство ряда распределения На рис. 4.1 показан многоугольник (полигон) распределения случайной величины, распределенной по закону Пуассона Р(Х=m)=Рm(λ) с параметрами λ = 0,5, λ = 1, λ = 2, λ = 3,5. Теорема. Математическое oжидaниe и дисперсия случайной величины, распределенной по закону Пуассона, совпадают и равны параметру λ этого закона, т.е.
20. Математическое ожидание и дисперсия числа и частости наступлений события в п повторных независимых испытаниях (с выводом). Математическое ожидание частости
□ Частость события
21. Определение нормального закона распределения. Теоретико-вероятностный смысл его параметров. Нормальная кривая и зависимость ее положения и формы от параметров. Определение. Непрерывная случайная величина Х имеет нормальный закон распределения (закон Гаусса) с параметрами а и
Термин «нормальный» не совсем удачный. Многие признаки подчиняются нормальному закону, например, рост человека, дальность полета снаряда и т.п. Но если какой-либо признак подчиняется другому, отличному от нормального, закону распределения, то это вовсе не говорит о «ненормальности» явления, связанного с этим признаком. Кривую нормального закона распределения называют нормальной или гауссовой кривой. На рис. 4.5 а, б приведены нормальная кривая Обратим внимание на то, что нормальная кривая симметрична относительно прямой х=а, имеет максимум в точке х=а, равный Можно заметить, что в выражении плотности нормального закона параметры обозначены буквами а и Теорема. Математическое ожидание случайной величины Х, распределенной по нормальному закону, равно параметру а этого закона, т.е. □ Математическое ожидание случайной величины Х:
(первый интеграл равен нулю как интеграл от нечетной функции по симметричному относительно начала координат промежутку, а второй интеграл Дисперсия случайной величины Х:
Сделаем ту же замену переменной
Применяя метод интегрирования по частям, получим:
Выясним, как будет меняться нормальная кривая при изменении параметров а и
Нормальный закон распределения случайной величины с параметрами а=0, 22. Функция распределения нормально распределенной случайной величины и ее выражение через функцию Лапласа. Сложность непосредственного нахождения функции распределения случайной величины, распределенной по нормальному закону, и вероятности ее попадания на некоторый промежуток связана с тем, что интеграл является «неберущимся». В элементарных функциях. Поэтому их выражают через функцию:
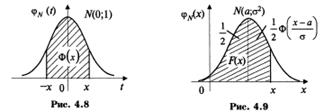
- функцию (интеграл вероятностей) Лапласа, для которой составлены таблицы. Геометрически функция Лапласа представляет собой площадь под стандартной нормальной кривой на отрезке [-х; х] (рис. 4.8).
Теорема. Функция распределения случайной величины Х, распределенной по нормальному закону, выражается через функцию Лапласа Ф(х) по формуле:
□ По формуле Сделаем замену переменной, полагая
Первый интеграл
(В силу четности подынтегральной функции и того, что интеграл Эйлера-Пуассона равен Второй интеграл с учетом Итак, 23. Формулы для определения вероятности: а) попадания нормально распределенной случайной величины в заданный интервал; б) ее отклонения от математического ожидания. Правило «трехсигм». Свойства случайной величины, распределенной по нормальному закону: 1. Вероятность попадания случайной величины Х, распределенной по нормальному закону, в интервал Где □ Учитывая, что вероятность
Вероятность того, что отклонение случайной величины Х, распределенной по нормальному закону, от математического ожидания а не превысит величину (по абсолютной величине), равна, где. □
«правило трех сигм»: Если случайная величина Х имеет нормальный закон распределения с параметрами а и Нарушение «правила трех сигм», т.е. отклонение нормально распределенной случайной величины Х больше, чем на
24. Понятие двумерной (/7-мерной) случайной величины. Примеры. Таблица ее распределения. Одномерные распределения ее составляющих. Условные распределения и их нахождение по таблице распределения. Очень часто результат испытания характеризуется не одной СВ, а некоторой системой случайных величин 1. Успеваемость выпускника вуза характеризуется системой n случайных величин 2. Погода в данном месте в определенное время суток может быть охарактеризована системой случайных величин: Любая СВ т.е. каждому элементарному событию ω ставится в соответствие несколько действительных чисел Случайные величины
Так как события Распределение одномерной случайной величины Х можно получить, вычислив вероятность события
Аналогично Т.о., чтобы по таблице распределения (табл. 5.1) найти вероятность того, что одномерная случайная величина примет определенное значение, надо просуммировать вероятности Если зафиксировать значение одного из аргументов, например, положить
Аналогично условное распределение СВ У при условии 25. Ковариация и коэффициент корреляции случайных величин. Связь между екоррелированностью и независимостью случайных величин. Пусть имеется двумерная СВ (Х,Y), распределение которой известно, т.е. известна табл. 5.1 или совместная плотность вероятности Определение. Ковариацией (или корреляционным моментом) Кху случайных величин Х и Y называется математическое ожидание произведения отклонений этих величин от своих математических ожиданий, т.е.
|

 .
. . ☻
. ☻ На рис. 3.7 показана Функция распределения непрерывной случайной величины Х, дифференцируемая во всех точках, кроме трех точек излома.
На рис. 3.7 показана Функция распределения непрерывной случайной величины Х, дифференцируемая во всех точках, кроме трех точек излома.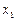 случайной величины Х вероятность
случайной величины Х вероятность  . Представим
. Представим  в виде
в виде  .
. . ☻
. ☻ не зависит от того, является этот интервал открытым или закрытым, т.е.
не зависит от того, является этот интервал открытым или закрытым, т.е.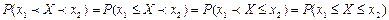 .
.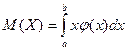 . Если возможные значения случайной величины рассматриваются на всей числовой оси, то математическое ожидание находится по формуле:
. Если возможные значения случайной величины рассматриваются на всей числовой оси, то математическое ожидание находится по формуле:  . При этом предполагается, что интеграл абсолютно сходится.
. При этом предполагается, что интеграл абсолютно сходится. .
. .
. непрерывной случайной величины Х называется производная ее функции распределения
непрерывной случайной величины Х называется производная ее функции распределения
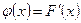
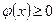 .
.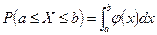 .
. ☺ Согласно свойству 4 функции распределения
☺ Согласно свойству 4 функции распределения 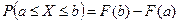 . Так как F(x) - первообразная для плотности вероятности
. Так как F(x) - первообразная для плотности вероятности 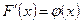 , то по формуле Ньютона-Лейбница приращение первообразной на отрезке [а,b] – определенный интеграл
, то по формуле Ньютона-Лейбница приращение первообразной на отрезке [а,b] – определенный интеграл  . ☻
. ☻
 .
.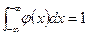 .
.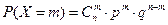 ,
,
 выполнено, ибо
выполнено, ибо 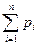 есть не что иное, как сумма всех членов разложения бинома Ньютона:
есть не что иное, как сумма всех членов разложения бинома Ньютона: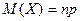 а ее дисперсия
а ее дисперсия 

 ,
,
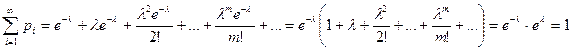 .
. и
и 
 события в n независимых испытаниях, в каждом из которых оно может наступить с одной и той же вероятностью р, равно р, т.е.
события в n независимых испытаниях, в каждом из которых оно может наступить с одной и той же вероятностью р, равно р, т.е. 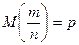 а ее дисперсия
а ее дисперсия  .
.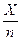 , т.е.
, т.е. 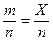 , где Х - случайная величина, распределенная по биномиальному закону. Поэтому
, где Х - случайная величина, распределенная по биномиальному закону. Поэтому .
. 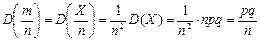 ■
■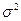 , если ее плотность вероятности имеет вид:
, если ее плотность вероятности имеет вид: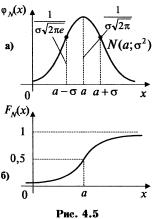

 с параметрами а и
с параметрами а и 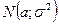 , и график функции распределения случайной величины Х, имеющей нормальный закон.
, и график функции распределения случайной величины Х, имеющей нормальный закон. , т.е.
, т.е.  , и две точки перегиба
, и две точки перегиба 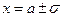 с ординатой
с ординатой  .
.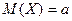 , а ее дисперсия - параметру
, а ее дисперсия - параметру 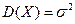 .
.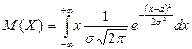 . Произведем замену переменной, положив
. Произведем замену переменной, положив 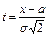 . Тогда
. Тогда 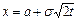 и
и 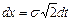 , пределы интегрирования не меняются и, следовательно,
, пределы интегрирования не меняются и, следовательно, 
 .
. - интеграл ЭйлераПуассона).
- интеграл ЭйлераПуассона).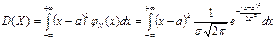 .
. , как и при вычислении предыдущего интеграла. Тогда
, как и при вычислении предыдущего интеграла. Тогда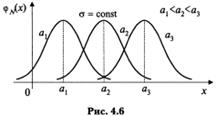
 .
. .■
.■ ). Если
). Если 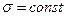 , и меняется параметр а (
, и меняется параметр а (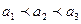 ), т.е. центр симметрии распределения, то нормальная кривая будет смещаться вдоль оси абсцисс, не меняя формы (рис. 4.6).
), т.е. центр симметрии распределения, то нормальная кривая будет смещаться вдоль оси абсцисс, не меняя формы (рис. 4.6).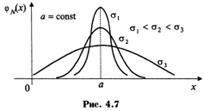 Если a=const и меняется параметр
Если a=const и меняется параметр  . При увеличении
. При увеличении 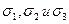 , где
, где  . Т.о., параметр а (он же математическое ожидание) характеризует положение Центра, а параметр
. Т.о., параметр а (он же математическое ожидание) характеризует положение Центра, а параметр  (он же дисперсия) - форму нормальной кривой.
(он же дисперсия) - форму нормальной кривой. .
.
 .
.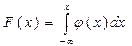 функция распределения:
функция распределения: 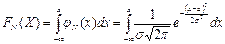 .
.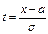 ,
,  ,
, 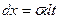 при
при  ,
,  , поэтому
, поэтому .
. .
. ).
).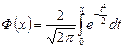 составляет
составляет 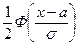 .
. . ■
. ■ , равна
, равна 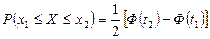 ,
, ,
, 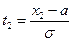 .
.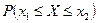 есть приращение функции распределения на отрезке
есть приращение функции распределения на отрезке  получим:
получим: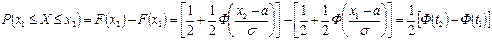 . ■
. ■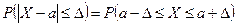 . Учитывая свойство 1, а также свойство нечетности функции Лапласа, получим
. Учитывая свойство 1, а также свойство нечетности функции Лапласа, получим . ■
. ■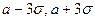 ).
).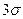 (по абсолютной величине), является событием практически невозможным, так как его вероятность весьма мала:
(по абсолютной величине), является событием практически невозможным, так как его вероятность весьма мала: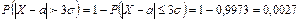 .
. , которую называют также многомерной (n-мерной) случайной величиной или случайным вектором Х = (
, которую называют также многомерной (n-мерной) случайной величиной или случайным вектором Х = ( - оценками по различным дисциплинам, проставленными в приложении к диплому.
- оценками по различным дисциплинам, проставленными в приложении к диплому. - температура;
- температура;  - влажность;
- влажность;  - давление;
- давление;  - скорость ветра и т.п.
- скорость ветра и т.п.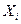 (i = 1,2,...,n) есть функция элементарных событий ω, входящих в пространство элементарных событий Ω (
(i = 1,2,...,n) есть функция элементарных событий ω, входящих в пространство элементарных событий Ω ( ). Поэтому и многомерная случайная величина есть функция элементарных событий ω:
). Поэтому и многомерная случайная величина есть функция элементарных событий ω: 
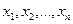 , которые приняли случайные величины
, которые приняли случайные величины  Наиболее полным описанием многомерной СВ является закон ее распределения. При конечном множестве возможных значений многомерной СВ такой закон может быть задан в форме таблицы (матрицы), содержащей всевозможные сочетания значений каждой из одномерных случайных величин, входящих в систему, и соответствующие им вероятности. Так, если рассматривается двумерная дискретная случайная величина (X,Y), то ее двумерное распределение можно представить в виде таблицы (матрицы) распределения (табл. 5.1), в каждой клетке (i,j) которой располагаются вероятности произведения событий
Наиболее полным описанием многомерной СВ является закон ее распределения. При конечном множестве возможных значений многомерной СВ такой закон может быть задан в форме таблицы (матрицы), содержащей всевозможные сочетания значений каждой из одномерных случайных величин, входящих в систему, и соответствующие им вероятности. Так, если рассматривается двумерная дискретная случайная величина (X,Y), то ее двумерное распределение можно представить в виде таблицы (матрицы) распределения (табл. 5.1), в каждой клетке (i,j) которой располагаются вероятности произведения событий  .
. (i = 1,2,...,n; j = 1,2,...,m), состоящие в том, что СВ Х примет значение
(i = 1,2,...,n; j = 1,2,...,m), состоящие в том, что СВ Х примет значение 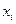 , а СВ Y - значение
, а СВ Y - значение 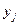 , несовместны и единственно возможны, т.е. образуют полную группу, то сумма их вероятностей равна единице, т.е.:
, несовместны и единственно возможны, т.е. образуют полную группу, то сумма их вероятностей равна единице, т.е.: 
 (i = 1,2,...,n) как сумму вероятностей несовместных событий:
(i = 1,2,...,n) как сумму вероятностей несовместных событий: .
. .
.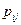 из соответствующей этому значению строки (столбца) данной таблицы.
из соответствующей этому значению строки (столбца) данной таблицы.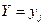 , то полученное распределение случайной СВ Х называется условным распределением Х при условии
, то полученное распределение случайной СВ Х называется условным распределением Х при условии  этого распределения будут условными вероятностями события
этого распределения будут условными вероятностями события 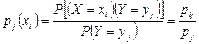 .
. .
.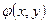 . Тогда можно найти математические ожидания М(Х) = ах, М(Y) = ау и дисперсии
. Тогда можно найти математические ожидания М(Х) = ах, М(Y) = ау и дисперсии  и
и 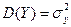 одномерных составляющих Х и Y. Однако математические ожидания и дисперсии случайных величин Х и Y недостаточно полно характеризуют двумерную случайную величину (Х,Y), т.к. не выражают степени зависимости ее составляющих Х и Y эту роль выполняют ковариация и коэффициент корреляции.
одномерных составляющих Х и Y. Однако математические ожидания и дисперсии случайных величин Х и Y недостаточно полно характеризуют двумерную случайную величину (Х,Y), т.к. не выражают степени зависимости ее составляющих Х и Y эту роль выполняют ковариация и коэффициент корреляции.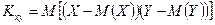 , Или
, Или  ,
,


