Закон распределения вероятностей случайной величины непрерывного типа равномерный, показательный(вид, параметры, свойства, типовые схемы практического приложения)Плотности распределений непрерывных случайных величин называют также законами распределений. Распределение вероятностей называют равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение.
Нормальный закон распределения. Функция плотности нормального распределения, параметры, приведение к стандартному виду, свойства. Функция нормального распределения, интеграл вероятности. Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью
Мы видим, что нормальное распределение определяется двумя параметрами: а иs. Достаточно знать эти параметры, чтобы задать нормальное распределение. Покажем, что вероятностный смысл этих параметров таков: а есть математическое ожидание, s—среднее квадратическое отклонение нормального распределения. а) По определению математического ожидания непрерывной случайной величины, M (X) = Введем новую переменную z = (x — а) / s. Отсюда x= s z+a, dx= s dz. Приняв во внимание, что новые пределы интегрирования равны старым, получим M (X) = Первое из слагаемых равно нулю (под знаком интеграла нечетная функция; пределы интегрирования симметричны относительно начала координат). Второе из слагаемых равно a (интеграл Пуассона Итак, М(Х) = а, т. е. математическое ожидание нормального распределения равно параметру а. б) По определению дисперсии непрерывной случайной величины, учитывая, что М (Х) = а, имеем D (X) = Введем новую переменную z = (x — а) / s. Отсюда х — a = s z, dx = s0 dz. Приняв во внимание, что новые пределы интегрирования равны старым, получим D (X) = Интегрируя по частям, положив u = z, dv= D (X) = s2. Следовательно, s(X) = Итак, среднее квадратическое отклонение нормального распределения равно параметру s.
13. До сих пор рассматривались случайные величины, возможные значения которых определялись одним числом. Такие величины называют одномерными. Например, число очков, которое может выпасть при бросании игральной кости,- дискретная одномерная величина; расстояние от орудия до места падения снаряда - непрерывная одномерная случайная величина. Кроме одномерных случайных величин изучают величины, возможные значения которых определяются двумя, тремя, …, п числами. Такие величины называются соответственно двумерными, трехмерными,..., n-мерными. Будем обозначать через (X, Y)двумерную случайную величину. Каждую из величин X и Y называют составляющей (компонентой); обе величины X и Y, рассматриваемые одновременно, образуют систему двух случайных величин. Аналогично n-мерную величину можно рассматривать как систему п случайных величин. Например, трехмерная величина (X, Y, Z)определяет систему трех случайных величин X, Y и Z. Законом распределения дискретной двумерной случайной величины называют перечень возможных значений этой величины, т. е. пар чисел (xi,yj)и их вероятностей p (xi,yj)(i= 1, 2 ,....,n; j = 1, 2 ,....,n). Обычно закон распределения задают в виде таблицы с двойным входом. Первая строка таблицы содержит все возможные значения составляющей X,а первый столбец — все возможные значения составляющей Y. В клетке, стоящей на пересечении «столбца хi»и «строки уj»,указана вероятность p (xi,yj)того, что двумерная случайная величина примет значение (xi,yj). Так как события (Х=xi, Y=yj)(i= 1, 2 ,....,n; j = 1, 2 ,....,n)образуют полную группу то сумма вероятностей, помещенных во все клетки таблицы, равна еденицы.
Таблица 2
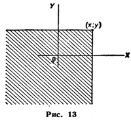
Зная закон распределения двумерной дискретной случайной величины, можно найти законы распределения каждой из составляющих. Действительно, например, события (Х=х 1, Y=у 1), (Х=х 1, Y=у 2),.... (Х = x 1, Y=ут)несовместны, поэтому вероятность Р (х 1) того, что X примет значение х 1, по теореме сложения такова: Р (х 1) = р (х 1, у 1) + р (х 1, у 2) +...+р (х 1, ут). Таким образом, вероятность того, что X примет значение х 1 равна сумме вероятностей «столбца х 1». В общем случае, для того чтобы найти вероятность Р (X =xi), надо просуммировать вероятности столбца xi. Аналогично сложив вероятности «строки yj», получим вероятность P (Y=yi). Рассмотрим прямоугольник ABCD со сторонами, параллельными координатным осям (рис. 15). Пусть уравнения сторон таковы: Х = х 1, Х = x 2, Y = у 1и Y= у 2. Найдем вероятность попадания случайной точки (Х; Y) в этот прямоугольник. Искомую вероятность можно найти, например, так: из вероятности попадания случайной точки в полуполосу АВ с вертикальной штриховкой (эта вероятность равна F (x 2 ,y 2) - F (x 2 ,y 1)) вычесть вероятность попадания точки в полуполосу СD с горизонтальной штриховкой (эта вероятность равна F (х 2, y 1) - F (х 1, y 1)): Р (х 1 ≤ X < х 2, у 1 ≤ Y < у 2) = [F (x 2, у 2) - - F (x 1, у 2) ] - [F (x 2, у 1) - F (x 1, у 1) ] (*) 14. Законом распределения дискретной двумерной случайной величины называют перечень возможных значений этой величины, т. е. пар чисел (xi,yj)и их вероятностей p (xi,yj)(i= 1, 2 ,....,n; j = 1, 2 ,....,n). Обычно закон распределения задают в виде таблицы с двойным входом.ервая строка таблицы содержит все возможные значения составляющей X,а первый столбец — все возможные значения составляющей Y. В клетке, стоящей на пересечении «столбца хi»и «строки уj»,указана вероятность p (xi,yj)того, что двумерная случайная величина примет значение (xi,yj). Так как события (Х=xi, Y=yj)(i= 1, 2 ,....,n; j = 1, 2 ,....,n)образуют полную группу то сумма вероятностей, помещенных во все клетки таблицы, равна еденицы.
Таблица 2
Зная закон распределения двумерной дискретной случайной величины, можно найти законы распределения каждой из составляющих. Действительно, например, события (Х=х 1, Y=у 1), (Х=х 1, Y=у 2),.... (Х = x 1, Y=ут)несовместны, поэтому вероятность Р (х 1) того, что X примет значение х 1, по теореме сложения такова: Р (х 1) = р (х 1, у 1) + р (х 1, у 2) +...+р (х 1, ут). Таким образом, вероятность того, что X примет значение х 1 равна сумме вероятностей «столбца х 1». В общем случае, для того чтобы найти вероятность Р (X =xi), надо просуммировать вероятности столбца xi. Аналогично сложив вероятности «строки yj», получим вероятность P (Y=yi).
Функцией распределения двумерной случайной величины (X, Y)называют функцию F (x, у), определяющую для каждой пары чисел x, у вероятность того, что X примет значение, меньшее x, и при этом Y примет значение, меньшее у:F (x, у) = Р (Х<x, Y<у). Геометрически это равенство можно истолковать так: F (x, у)есть вероятность того, что случайная точка (X, Y)попадет в бесконечный квадрант с вершиной (x, у), расположенный левее и ниже этой вершины. СВ-ВА Ф-ЙИИ РАСПРЕД.ДВУМЕР.СВ. 1. Значения функции распределения удовлетворяют двойному неравенству 0 ≤F (x,y,) ≤;1; 2. F (х, у) есть неубывающая функция по каждому аргументу, т.е. F (x 2 ,y,) ≥ F (x 1 ,y,)если х 2 > х 1; F (x,y 2) ≥ F (x,y 1), если у 2 > у 1. 1) X примет значение, меньшее х 1, и при этом Y < у с вероятностью Р (X < х 1, Y < у); 2) X примет значение, удовлетворяющее неравенству х 1 ≤Х <х 2, и при этом Y < у с вероятностью Р (х 1 ≤Х <х 2, Y <у). 3. Имеют место предельные соотношения: 1) F (-∞, y) = 0,2) F (x, -∞;) = 0, 3) F (-∞, -∞;) = 0, 4) F (∞, ∞;) = 1. Зная плотность совместного распределения f (x,у), можно найти функцию распределения F (x,у)по формуле:
15. Двумерная случайная величина задавалась с помощью функции распределения. Непрерывную двумерную величину можно также задать, пользуясь плотностью распределения. Здесь и далее будем предполагать, что функция распределения F (x,у)всюду непрерывна и имеет всюду (за исключением, быть может, конечного числа кривых) непрерывную частную производную второго порядка. Плотностью совместного распределения вероятностей f (x,у) двумерной непрерывной случайной величины (X,Y) называют вторую смешанную частную производную от функции распределения: Зная плотность совместного распределения f (x,у), можно найти функцию распределения F (x,у)по формуле: Известно, что если события А и В зависимы, то условная вероятность события В отличается от его безусловной вероятности. В этом случае (см. гл. III, § 2)
Аналогичное положение имеет место и для случайных величин. Для того чтобы охарактеризовать зависимость между составляющими двумерной случайной величины, введем понятие условного распределения. Рассмотрим дискретную двумерную случайную величину (X,Y). Пусть возможные значения составляющих таковы: х 1 х 2,.... хп; у 1, у 2..., ут. Допустим, что в результате испытания величина Y приняла значение Y= у 1; при этом X примет одно из своих возможных значений: х 1, или х 2,..., или хn. Обозначим условную вероятность того, что X примет, например, значение х 1при условии, что Y=у 1, через р (х 1 |у 1). Эта вероятность, вообще говоря, не будет равна безусловной вероятности р (х 1). В общем случае условные вероятности составляющей будем обозначать так: p (xi|yj)(i= 1, 2, …, n; j= 1, 2, …, m). Условным распределением составляющей X при Y=у 1называют совокупность условных вероятностей p (x 1 |yj), p (x 2 |yj), …, p (xn|yj)вычисленных в предположении, что событие Y=уj (j имеет одно и то же значение при всех значениях X)уже наступило. Аналогично определяется условное распределение составляющей Y.. Отыскание плотностей вероятности составляющих двумерной случайной величины. Пусть известна плотность совместного распределения вероятностей системы двух случайных величин. Найдем плотности распределения каждой из составляющих. Найдем сначала плотность распределения составляющей X. Обозначим через F 1(x)функцию распределения, составляющей X. По определению плотности распределения одномерной случайной величины, Приняв во внимание соотношения Аналогично находим плотность распределения составляющей Y: Итак, плотность распределения одной из составляющих равна несобственному интегралу с бесконечными пределами от плотности совместного распределения системы, причем переменная интегрирования соответствует другой составляющей. Зная закон распределения двумер ной дискретной случайной величины, можно, пользуясь формулой (*), вычислить условные законы распределения составляющих. Например, условный закон распределения X в предположении, что событие Y=у 1уже произошло, может быть найден по формуле
Аналогично находят условные законы распределения составляющей Y:
Условные законы распределения составляющих системы непрерывных случайных величин.Пусть (X, Y)- непрерывная двумерная случайная величина. Условной плотностью
Запишем формулы (*) и (**) в виде Отсюда заключаем: умножая закон распределения одной из составляющих на условный закон распределения другой составляющей, найдем закон распределения системы случайных величин. Как и любая плотность распределения, условные плотности обладают следующими свойствами:
16. Теорема 1. Корреляционный момент двух независимых случайных величин X и Y равен нулю. μху= М {[Х - М (X) ][Y - M (Y) ]} = М [Х-М (X) ]M[Y - M (Y) ]= 0. Из определения корреляционного момента следует, что он имеет размерность, равную произведению размерностей величин X и Y. Другими словами, величина корреляционного момента зависит от единиц измерения случайных величин. По этой причине для одних и тех же двух величин величина корреляционного момента имеет различные значения в зависимости от того, в каких единицах были измерены величины. Две случайные величины X и Y называют коррелированными, если их корреляционный момент (или, что то же, коэффициент корреляции) отличен от нуля; X и Y называют некоррелированными величинами, если их корреляционный момент равен нулю. Две коррелированные величины также и зависимы. Действительно, допустив противное, мы должны заключить, что μху =0, а это противоречит условию, так как для коррелированных величин μху ≠0. Обратное предположение не всегда имеет место, т. е. если две величины зависимы, то они могут быть как коррелированными, так и некоррелированными. Другими словами, корреляционный момент двух зависимых величин может быть не равен нулю, но может и равняться нулю. На практике часто встречаются двумерные случайные величины, распределение которых нормально. Нормальным законом распределения на плоскости называют распределение вероятностей двумерной случайной величины (X, Y), если
Мы видим, что нормальный закон на плоскости определяется пятью параметрами: а 1, а 2, σх, σу и rху. Можно доказать, что эти параметры имеют следующий вероятностный смысл: а 1, а 2- математические ожидания, σх, σу - средние квадратические отклонения, rху - коэффициент корреляции величин X и Y. Убедимся в том, что если составляющие двумерной нормально распределенной случайной величины некоррелированны, то они и независимы. Действительно, пусть X и Y некоррелированны. Тогда, полагая в формуле (*) rxy= 0, получим
Таким образом, если составляющие нормально распределенной случайной величины некоррелированны, то плотность совместного распределения системы равна произведению плотностей распределения составляющих, а отсюда и следует независимость составляющих (см. § 16). Справедливо и обратное утверждение (см. § 18). Итак, для нормально распределенных составляющих двумерной случайной величины понятия независимости и некоррелированности равносильны. Рассмотрим прямоугольник ABCD со сторонами, параллельными координатным осям (рис. 15). Пусть уравнения сторон таковы: Х = х 1, Х = x 2, Y = у 1и Y= у 2. Найдем вероятность попадания случайной точки (Х; Y) в этот прямоугольник. Искомую вероятность можно найти, например, так: из вероятности попадания случайной точки в полуполосу АВ с вертикальной штриховкой (эта вероятность равна F (x 2 ,y 2) - F (x 2 ,y 1)) вычесть вероятность попадания точки в полуполосу СD с горизонтальной штриховкой (эта вероятность равна F (х 2, y 1) - F (х 1, y 1)): Р (х 1 ≤ X < х 2, у 1 ≤ Y < у 2) = [F (x 2, у 2) - - F (x 1, у 2) ] - [F (x 2, у 1) - F (x 1, у 1) ] (*)
18. Во многих задачах требуется установить и оценить зависимость изучаемой случайной величины Y от одной или нескольких других величин. Рассмотрим сначала зависимость Y от одной случайной (или неслучайной) величины X, а затем от нескольких величин (см. § 15). Две случайные величины могут быть связаны либо функциональной зависимостью (см. гл. XII, § 10), либо зависимостью другого рода, называемой статистической, либо быть независимыми. Строгая функциональная зависимость реализуется редко, так как обе величины или одна из них подвержены еще действию случайных факторов, причем среди них могут быть и общие для обеих величин (под «общими» здесь подразумеваются такие факторы, которые воздействуют и на Y и на X). В этом случае возникает статистическая зависимость. Например, если Y зависит от случайных факторов Z1, Z2, V1, V2, а X зависит от случайных факторов Z1, Z2, U1, то между Y и Х имеется статистическая зависимость, так как среди случайных факторов есть общие, а именно: Z1, Z2. Статистической называют зависимость, при которой изменение одной из величин влечет изменение распределения другой. В частности, статистическая зависимость проявляется в том, что при изменении одной из величин изменяется среднее значение другой; в этом случае статистическую зависимость называют корреляционной. Приведем пример случайной величины Y, которая не связана с величиной Х функционально, а связана корреляционно. Пусть Y—урожай зерна, X— количество удобрений. С одинаковых по площади участков земли при равных количествах внесенных удобрений снимают различный урожай, т. е. Y не является функцией от X. Это объясняется влиянием случайных факторов (осадки, температура воздуха и др.). Вместе с тем, как показывает опыт, средний урожай является функцией от количества удобрений, т. е. Y связан с Х корреляционной зависимостью.
18. Для описания системы двух случайных величин кроме математических ожиданий и дисперсий составляющих используют и другие характеристики; к их числу относятся корреляционный момент и коэффициент корреляции. Корреляционным моментом μху случайных величин X и Y называют математическое ожидание произведения отклонений этих величин: μху={M[X-M (X) ][Y-M (Y) ]},Для вычисления корреляционного момента дискретных величин используют формулу
а для непрерывных величин - формулу Корреляционный момент служит для характеристики связи между величинами X и Y. Как будет показано ниже, корреляционный момент равен нулю, если X и Y независимы; следовательно, если корреляционный момент не равен нулю, то X и Y - зависимые случайные величины. Замечание 1. Учитывая, что отклонения есть центрированные случайные величины, корреляционный момент можно определить как математическое ожидание произведения центрированных случайных величин: μху=M[ Теорема 1. Корреляционный момент двух независимых случайных величин X и Y равен нулю. Доказательство. Так как X и Y - независимые случайные величины, то их отклонения X - М (X)и Y - М (Y)также независимы. Пользуясь свойствами математического ожидания (математическое ожидание произведения независимых случайных величин равно произведению математических ожиданий сомножителей) и отклонения (математическое ожидание отклонения равно нулю), получим μху= М {[Х - М (X) ][Y - M (Y) ]} = М [Х-М (X) ]M[Y - M (Y) ]= 0. Из определения корреляционного момента следует, что он имеет размерность, равную произведению размерностей величин X и Y. Другими словами, величина корреляционного момента зависит от единиц измерения случайных величин. По этой причине для одних и тех же двух величин величина корреляционного момента имеет различные значения в зависимости от того, в каких единицах были измерены величины. Пусть, например, X и Y были измерены в сантиметрах и μху = 2 см2; если измерить X и Y в миллиметрах, то μху = 200мм. Такая особенность корреляционного момента является недостатком этой числовой характеристики, поскольку сравнение корреляционных моментов различных систем случайных величин становится затруднительным. Для того чтобы устранить этот недостаток, вводят новую числовую характеристику - коэффициент корреляции. Коэффициентом корреляции rху случайных величин X и Y называют отношение корреляционного момента к произведению средних квадратических отклонений этих величин: rху= μху/ (σx σy). (*) Так как размерность μху равна произведению размерностей величин X и Y, σх имеет размерность величины X, σy имеет размерность величины Y (см. гл. VIII, § 7), то rху - безразмерная величина. Таким образом, величина коэффициента корреляции не зависит от выбора единиц измерения случайных величин. В этом состоит преимущество коэффициента корреляции перед корреляционным моментом. Очевидно, коэффициент корреляции независимых случайных величин равен нулю (так как μху = 0). Замечание 3. Во многих вопросах теории вероятностей целесообразно вместо случайной величины X рассматривать нормированную случайную величину X’, которую определяют как отношение отклонения к среднему квадратическому отклонению: X’= (X-M (X)) / σx. Нормированная величина имеет математическое ожидание, равное нулю, и дисперсию, равную единице. Действительно, используя свойства математического ожидания и дисперсии, имеем:
Легко убедиться, что коэффициент корреляции rху равен корреляционному моменту нормированных величин X’ и Y’:
Теорема 2. Абсолютная величина корреляционного момента двух случайных величин X и Y не превышает среднего геометрического их дисперсий: Доказательство. Введем в рассмотрение случайную величину Z 1 =σyX—σxY и найдем ее дисперсию D (Z 1) = M[Z 1 —mz] 2. Выполнив выкладки, получим D (Z 1) = 2 μху ≤ σx σy. (**) Введя случайную величину Z 1 =σvX +σxY, аналогично найдем μху≥ - σx σy. (***) Объединим (**) и (***): - σx σy≤ μху ≤ σx σy, (****) или
Итак,
Теорема 3. Абсолютная величина коэффициента корреляции не превышает единицы: rху ≤1. Доказательство: Разделим обе части двойного неравенства (****) на произведение положительных чисел σx σy, - 1 ≤ rху ≤;1. Итак, rху≤;1. Статистической называют зависимость, при которой изменение одной из величин влечет изменение распределения другой. В частности, статистическая зависимость проявляется в том, что при изменении одной из величин изменяется среднее значение другой; в этом случае статистическую зависимость называют корреляционной. Приведем пример случайной величины Y, которая не связана с величиной Х функционально, а связана корреляционно. Пусть Y—урожай зерна, X— количество удобрений. С одинаковых по площади участков земли при равных количествах внесенных удобрений снимают различный урожай, т. е. Y не является функцией от X. Это объясняется влиянием случайных факторов (осадки, температура воздуха и др.). Вместе с тем, как показывает опыт, средний урожай является функцией от количества удобрений, т. е. Y связан с Х корреляционной зависимостью. 19. Рассмотрим двумерную случайную величину (X,Y), где X и Y - зависимые случайные величины. Представим одну из величин как функцию другой. Ограничимся приближенным представлением (точное приближение, вообще говоря, невозможно) величины Y в виде линейной функции величины X:
где Функцию
Учитывая, что М (X—тх) =М (Y— my)= 0, M[ (X—mx) * (Y-my) ]= μху=r σxσy, и выполнив выкладки, получим
Исследуем функцию
Отсюда
Легко убедиться, что при этих значениях Итак, линейная средняя квадратическая регрессия Y и X имеет вид
или
Коэффициент
называют прямой среднеквадратической регрессии Y на X. Подставив найденные значения Итак, если коэффициент корреляции r = ± 1, то Y и X связаны линейной функциональной зависимостью.
Аналогично можно получить прямую среднеквадратической регрессии X на Y:
( Если r = ±1, то обе прямые регрессии, как видно из (**) и (***), совпадают. Из уравнений (**) и (***) следует, что обе прямые регрессии проходят через точку (тх, m у), которую называют центром совместного распределения величин X и Y. В гл. XIV, § 15 были введены уравнения регрессии Y на Х и Х на Y: М(У|х)=f(х), М(Х|у)=φ(у). Условное математическое ожидание М (Y | х) является функцией от х, следовательно, его оценка, т. е. условное среднее Для описания системы двух случайных величин кроме математических ожиданий и дисперсий составляющих используют и другие характеристики; к их числу относятся корреляционный момент и коэффициент корреляции. Корреляционным моментом μху случайных величин X и Y называют математическое ожидание произведения отклонений этих величин: μху={M[X-M (X) ][Y-M (Y) ]},Для вычисления корреляционного момента дискретных величин используют формулу
Корреляционный момент служит для характеристики связи между величинами X и Y. Как будет показано ниже, корреляционный момент равен нулю, если X и Y независимы; следовательно, если корреляционный момент не равен нулю, то X и Y - зависимые случайные величины. Замечание 1.
Дата добавления: 2015-08-12; просмотров: 1019. Нарушение авторских прав; Мы поможем в написании вашей работы! Шрифт зодчего Шрифт зодчего состоит из прописных (заглавных), строчных букв и цифр... Картограммы и картодиаграммы Картограммы и картодиаграммы применяются для изображения географической характеристики изучаемых явлений... Практические расчеты на срез и смятие При изучении темы обратите внимание на основные расчетные предпосылки и условности расчета... Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...
Предпосылки, условия и движущие силы психического развития Предпосылки –это факторы. Факторы психического развития –это ведущие детерминанты развития чел. К ним относят: среду...
Броматометрия и бромометрия Броматометрический метод основан на окислении восстановителей броматом калия в кислой среде...
|
).
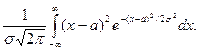
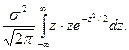
, найдем
.
Рассмотрим двумерную случайную величину ( X, Y ) (безразлично, дискретную или непрерывную).Пусть x, у -пара действительных чисел. Вероятность события, состоящего в том, что X примет значение, меньшее x, и при этом Y примет значение, меньшее у, обозначим через F (x, у). Если x и у будут изменяться, то, вообще говоря, будет изменяться и F (х, у), т.е. F (x, у)-есть функция от x и у.
.. что непосредственно следует из определения плотности распределения двумерной непрерывной случайной величины (X, У).
Геометрически эту функцию можно истолковать как поверхность, которую называют поверхностью распределения.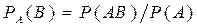
. (*)
.
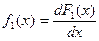, найдем 
. Продифференцировав обе части этого равенства по x, получим 
, или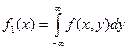 
. (*)
. (**)
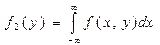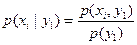(i= 1, 2, …, n).В общем случае условные законы распределения составляющей X определяются соотношением
(**)
. (***)
(x|у)распределения составляющих X при данном значении Y = у называют отношение плотности совместного распределения f (x,у)системы (X,Y)к плотности распределения f 2(y) составляющей Y: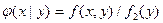 
. (*)Подчеркнем, что отличие условной плотности φ(x|у)от безусловной плотности f 1 (x)состоит в том, что функция φ(x|у) дает распределение X при условии, что составляющая Y приняла значение Y = у; функция же f 1 (x)дает распределение X независимо от того, какие из возможных значений приняла составляющая Y. Аналогично определяется условная плотность составляющей Y при данном значении Х = x: 
. (**) Если известна плотность совместного распределения f (х, у), то условные плотности составляющих могут быть найдены в силу (*) и (**) (см. § 12) по формулам:
, (***)
. (****)
, 
.
; 
.
(*)
.
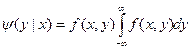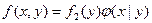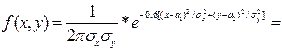
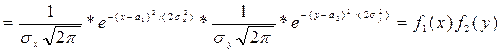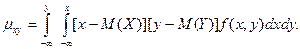
]. 3амечание 2. Легко убедиться, что корреляционный момент можно записать в виде μху=M (XY) -M (X) M (Y).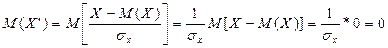
;
.
.
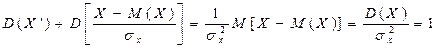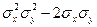μху. Любая дисперсия неотрицательна, поэтому 2 
.
.
,
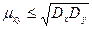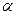и 
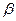- параметры, подлежащие определению. Это можно сделать различными способами: наиболее употребительный из них - метод наименьших квадратов.
называют «наилучшим приближением» Y в смысле метода наименьших квадратов, если математическое ожидание М [Y — g (X) ] 2принимает наименьшее возможное значение; функцию g (x)называют среднеквадратической регрессией Y на X. Теорема. Линейная средняя квадратическая регрессия Y на X имеет вид 
, где тх=M (X), тy=M (Y),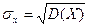 
, 
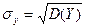, r = μху /(σxσy) - коэффициент корреляции величин X и Y. Доказательство. Введем в рассмотрение функцию двух независимых аргументов 
.
.
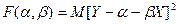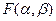на экстремум, для чего приравняем нулю частные производные:
, 
.
,
.
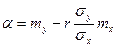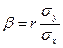называют коэффициентом регрессии Y на X, а прямую
(**)
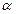и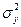 
(1 - r 2). Величину 
(***)
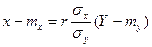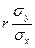- коэффициент регрессии X на Y) и остаточную дисперсию 
(1 - r 2)величины X относительно Y.
, также функция от х; обозначив эту функцию через f* (х), получим уравнение 
= φ*(y) называют выборочным уравнением регрессии Х на Y; функцию φ*(y) называют выборочной регрессией Х на Y, а ее график—выборочной линией регрессии Х на Y. Как найти по данным наблюдений параметры функций f*(х) и φ*(y), если вид их известен? Как оценить силу (тесноту) связи между величинами Х и Y и установить, коррелированы ли эти величины? Ответы на эти вопросы изложены ниже
