Числа зубьев зацепляющихся колес, нарезанных долбяком
Примечание: z 1, z 2 – число зубьев меньшего колеса и большего колеса соответственно.
Условие соосности. Сущность условия соосности заключается в том, что оси центральных колес 1, 3 и водила Н должны лежать на одной прямой, т.е. колеса 1, 3 и водило Н должны быть соосными. Условие соосности выражается через радиусы начальных окружностей (рис.4.13) для схем: · 1 – r 1+ r 2 = r 3- r 2; · 2 – r 1+ r 2 = r 3- r 2'; · 3 – r 1+ r 2 = r 3+ r 2'; · 4 – r 1- r 2 = r 3- r 2'. Для нулевых зубчатых колес радиусы начальных окружностей вычисляются по формуле Обозначим m 1 – модуль зубчатых колес 1 и 2; m 2 – модуль зубчатых колес 2 ' и 3. Тогда для нулевых зубчатых колес условие соосности выражается через числа зубьев колес для схем: · 1 – z 1+ z 2 = z 3- z 2; · 2 – (z 1+ z 2) m 1 = (z 3- z 2') m 2; · 3 – (z 1+ z 2) m 1 = (z 3+ z 2') m 2; · 4 – (z 1- z 2) m 1 = (z 3- z 2') m 2. В случае, если m 1 = m 2: · 1 – z 3 = z 1 +2 z 2; · 2 – z 1+ z 2 = z 3- z 2'; · 3 – z 1+ z 2 = z 3+ z 2'; · 4 – z 1- z 2= z 3- z 2'. Условие соседства. Выигрыш в размерах у планетарного редуктора по сравнению с простой многоступенчатой передачей происходит также при применении нескольких сателлитов. В силовых редукторах располагают возможно большее число сателлитов, чтобы уменьшить нагрузку на каждую пару зубьев. Для несиловых передач увеличение числа сателлитов приводит к повышению плавности передачи. Максимальное число сателлитов, которые могут быть установлены, ограничивается условием отсутствия касания окружностей головок двух соседних сателлитов, т.е. условием соседства. В дифференциальных и планетарных механизмах сателлиты располагаются по окружности симметрично в одной плоскости так, чтобы соседние сателлиты не накладывались друг на друга или не задевали вершинами зубьев. Для условия соседства можно получить математическое выражение. На рис. 4.14 показаны два соседних сателлита в предельном положении, когда окружности их вершин не касаются друг друга. Соединив центры вращения колес, получим равнобедренный треугольник OO1O1', у которого Поскольку R = r 1+ r 2, а радиусы начальных окружностей равны Предельный случай (4.14), недопустим, так как при малейших неточностях сборки вершины зубьев начнут задевать друг друга. Поэтому между окружностями вершин сателлитов должен быть зазор, т.е. Для нулевых зубчатых колес
Рис. 4.14. К определению условия соседства
Число сателлитов или блоков сателлитов вычисляется в соответствии с выражением
Эта формула получена для внешнего зацепления. В случае внутреннего зацепления (рис. 4.15) аналогичным путем выводится неравенство при рассмотрении двух соседних сателлитов z 2 и центрального колеса z 3.
Рис. 4.15. К определению условия сборки Для двухрядных планетарных механизмов (см. рис. 4.13, схемы 2, 3, 4), у которых блок сателлитов состоит из двух колес 2 и 2 ', проверка условия соседства производится по сателлиту, имеющему больший радиус начальной окружности, и соединенному с ним центральному колесу. Определенное по неравенствам и округленное всегда в меньшую сторону число блоков сателлитов является максимально возможным для данного механизма при размещении сателлитов в одной плоскости. Таким образом, условие соседства выражается для схем:
· 1 –
· 2 –
· 3 –
· 4 – обычно у этих редукторов один блок сателлитов. Задача. Проверить, выполняется ли условие соседства сателлитов для механизма, соответствующего схеме 3 (рис. 4.13), при одинаковом модуле колес. Дано: К = 3 – число блоков сателлитов; число зубьев: z 1=45; z 2=18; z 3=46; z 2'=19; ha * = 1. Решение. Поскольку z 2' > z 2 проверку по условию соседства производим по внешнему зацеплению колес z 3 и z 2'.
т.е. число сателлитов по условию соседства может быть до 9. Следовательно, число сателлитов К =3 удовлетворяет условию соседства.
Условие сборки. Условие сборки (или условие равных углов между сателлитами) заключается в том, чтобы зубья каждого сателлита могли одновременно войти в зацепление с обоими центральными колесами при симметричном расположении зон зацепления (рис. 4.15). Планетарная передача может быть собрана в том случае, если головки зубьев сателлита 2 войдут во впадины центральных колес 1 и 3 одновременно, и при этом ось сателлита совпадет с осью соответствующего пальца на водиле. Допустим, что колесо 3 неподвижно. Расположим центральное колесо 1 таким образом, чтобы ось симметрии какой-либо впадины его совпадала с осью симметрии впадины колеса 3 (рис. 4.15). Тогда между колесами 1 и 3 можно установить сателлит. Для определенности примем, что сателлит имеет четное число зубьев. Если колесо 1 повернуть на один угловой шаг, т.е. на угол
где Учитывая, что Сателлиты могут быть установлены не в параллельных плоскостях, а в одной. Тогда для установки второго сателлита колесо 1 надо повернуть не на один угловой шаг,а на угол l ·τ1, где l – целое число. При этом Для редуктора Джемса (рис. 4.13, схема 1) максимальное число сателлитов в зависимости от передаточного отношения указано в табл. 4.2.
Таблица 4.2 Количество сателлитов в планетарном механизме Джемса
Условие сборки выражается для схем: · 1 – z 1+ z 3= k l;
· 2 – · 3 – Для схем 2 и 3 условие сборки представляется еще и так:
Поскольку условие сборки фактически сводится к проверке, будет ли при установке сателлитов целым числом интервал числа зубьев центрального колеса, то его выражают соотношением:
где z 1 – число зубьев центрального колеса; k – число сателлитов; В и l – целые числа (l = 1,2,3...; В = 0,1,2,3...).
Методика выбора числа зубьев в планетарных механизмах Проектирование планетарной передачи рекомендуется проводить в следующей последовательности: 1. Ознакомиться с исходными данными и условиями работы планетарного механизма; 2. Определить требуемое передаточное отношение между угловыми скоростями входного и выходного валов планетарной передачи; 3. Выбрать структурную схему механизма; 4. Используя формулу Виллиса, получить соотношение между передаточным отношением и числами зубьев колес; 5. Проанализировать ограничения, которые необходимо учитывать при выборе чисел зубьев колес; 6. Выбрать методику поиска наиболее подходящего варианта кинематической схемы планетарной передачи; 7. Методом перебора проанализировать несколько вариантов решения и дать им оценку; 8. Вычертить кинематическую схему спроектированной передачи в масштабе длины; 9. Построить треугольники распределения линейных скоростей звеньев и диаграмму угловых скоростей звеньев планетарного механизма; 10. Определить графически передаточное отношение спроектированного механизма и его отклонение от требуемого значения. Числа зубьев должны быть в практически осуществимых пределах (обычно от 18 до 100). При их назначении целесообразно руководствоваться рекомендациями, изложенными выше. В иных случаях все качественные показатели зубчатого зацепления (отсутствие интерференции, заострения и т.п.) обеспечиваются соответствующим выбором коэффициента смещения. Пример подбора чисел зубьев колес однорядного планетарного механизма
Для механизма Джемса (рис. 4.13, схема 1) значение передаточного отношения На основании ранее изложенного для планетарного механизма, соответствующего схеме 1: · передаточное отношение · условие соосности: z 3= z 1+2 z 2; · условие сборки сателлитов: · максимальное число сателлитов из условия соседства
Из формулы для передаточного отношения выражаем
Получаем общее уравнение для определения чисел зубьев однорядного планетарного механизма:
Решение этой задачи возможно в неопределенном числе вариантов, так как при трех неизвестных числах зубьев имеем два уравнения с дополнительными условиями сборок и соседства. Исходя из требований наименьших габаритов передачи и условия отсутствия подрезания, выбираем наименьшее число z 1 зубьев центрального колеса 1, а по заданному передаточному отношению Задача. Подобрать числа зубьев колес однорядного планетарного механизма. Дано: Решение. Подставляем значение
После вычислений получим Для обеспечения минимальных габаритов механизма при отсутствии подрезания или заклинивания передачи, согласно табл. 4.1 принимаем z 1=20. Тогда
откуда z 2 = 25, z 3 = 70. Максимальное возможное число сателлитов из условия соседства:
Практически k может быть равным 4,3 или 2. Принимаем k = 3, тогда последний член пропорции 90/ k = 30. Условие сборки при этом удовлетворяется, так как l = 30. Это означает, что каждый последующий сателлит устанавливается на место предыдущего при простом повороте водила на угол 360о/ k = 360°/3 = 120°, и повороте центрального колеса 1 на 30 угловых шагов. Задача. Для механизма по схеме 1 (рис. 4.13) подобрать числа зубьев, обеспечивающие передаточное отношение Решение: передаточное отношение механизма Находим число зубьев колеса 3: Проверяем выполнение условия соседства:
Проверяем условие сборки:
Произведенный расчет показывает, что подобранные числа зубьев при числе сателлитов k = 3 удовлетворяют условиям соосности, соседства и сборки. Задача. Спроектировать редуктор, передаточное отношение которого Выбор схемы редуктора: так как Возможен и другой вариант: последнюю ступень оставить планетарной, а в начале использовать простые ступени, причем, чтобы редуктор был соосным, их должно быть две (рис. 4.16, а).
Рис. 4.16. Ступени редуктора
Решение 1. Редуктор Джемса с двумя простыми ступенями (рис. 4.16, а). Наибольшей компактности можно достигнуть, если выдержать условие rа +2 rb = r 3. Можно допустить, что ra = rc = r 1. Из условия соосности r b = rd. Общее передаточное отношение равно:
При одинаковом модуле всех колес с учетом условия соосности
Принимаем za = zc = z 1 = 17. Тогда Чтобы найти zb, надо решить кубическое уравнение, поэтому определяем его подбором, учитывая, что эта величина может быть только целым числом. Если принять zb =40, то общее передаточное отношение Таким образом, при za = zc = z 1 = 17; zd = zb = 40; Определяем z 3: Из условия соосности Проверяем условие сборки:
Большее число сателлитов благоприятнее. Решение 2. Два последовательно соединенных механизма (рис. 4.16, б). Для упрощения изготовления редуктора возьмем одинаковые ступени:
Принимаем z 1=17. Тогда
Условие сборки: z I + z 3 = kl; 17 + 87 = 104. Можно принять k = 4, что при данном передаточное числе не нарушает условие соседства. По габаритным размерам (рис. 4.16) предпочтение следует отдать второму варианту. Выполним расчет КПД редуктора при условии, что к.п.д. каждой пары колес равен 0,96. Для трехступенчатого редуктора (рис. 4.16, а):
КПД планетарной ступени определяем по формуле
Общий КПД Для двухступенчатого редуктора (рис. 4.16, б):
Таким образом, схема редуктора, выполненная их двух планетарных ступеней, оказывается более выгодной по габаритным размерам и КПД. Для окончательной оценки обеих схем необходимо сравнить их также по себестоимости, которая зависит от количества деталей и узлов, точности их изготовления, веса деталей, качества применяемых материалов и др. Синтез планетарных передач по сложным схемамцелесообразно выполнять с применением ЭВМ для перебора всех возможных вариантов. Пример подбора чисел зубьев двухрядного планетарного механизма
Для механизма, соответствующего схеме 2 (рис. 4.13), значение передаточного отношения
Из уравнения следует, что Условие соосности: (z 1+ z 2) m 1=(z 3- z 2') m 2; (z 1+ z 2) m 1/ m 2 = z 3- z 2'. Условие сборки сателлитов:
Максимально возможное число блоков сателлитов из условия соседства:
Спроектировать механизм по схеме 2 можно, используя условие Левитской О.Н., согласно которому Методика обосновывается следующими рассуждениями. Передаточное отношение Отсюда
Из условия, что размер z 3 будет минимальным, т.е. Аналогично выводим формулу для определения числа зубьев z 2', так же полагая, что z 3 имеет минимальное значение:
Выражения для z 1 и z 2’ получаются совершенно одинаковыми. Следовательно, минимум величины z 3 при заданном При этом
Таким образом, получаем Значение z 2 округляют до целого числа, но чтобы удовлетворять заданному передаточному отношению, условиям соосности и соседства. Например, при
Из условия соосности z 3= z 1+ z 2+ z 2'=18+53+18=89. Число сателлитов из условия соседства
Принимаем k = 3. Условие сборки соблюдать необязательно, так как с центральными колесами входят в зацепление различные сателлиты. Поэтому перед закреплением второго сателлита на оси водила, его можно повернуть на нужный угол так, чтобы он вошел в зацепление со своим центральным колесом. Чаще всего, задача подбора чисел зубьев планетарного редуктора по схеме 2 заключается в составлении четырех уравнений для определения четырех неизвестных – чисел зубьев z 1, z 2, z 2' и z 3 колес механизма. Наиболее распространенным методом подбора чисел зубьев для планетарного механизма со сдвоенными сателлитами является метод сомножителей, при котором числа зубьев определяются только по двум условиям – передаточному отношению и условию соосности, а проверка производится по условиям сборки и соседства. Рассмотрим сущность этого метода. Из уравнения передаточного отношения схемы 2 Например, если
Из этих сомножителей следует выбрать такие, которые бы обеспечивали наиболее подходящую кинематическую схему передачи, например, по критерию минимальных размеров и массы зубчатых колес. Эти требования конкретизируются в каждом случае с учетом условий работы передачи. Принимаем соотношение С 2/ С 1 и С 3/ С 2' близкими к значению Выбираем комбинацию коэффициентов: C 1=5; C 2=29, С 2'=1; С 3=5. Тогда z 1= 5(5-l)γ = 20γ; z 2 =29(5-1)γ = 116γ; z 2'= l (5+29)γ = 34γ; z 3=5(5+29)γ = 170γ. При γ = 1 числа зубьев равны: z 1=20; z 2=116; z 2'=34; z 3=170 (целые числа). Проверяют на условие сборки при k = 3: Условие соседства
не выполняется, т.е. окружности вершин зубьев соседних сателлитов пересекаются между собой, что недопустимо. Анализируем второй вариант сомножителей: С 1 = 6, С 2=29, С 2'=1, С 3=6. Тогда z 1=6(6-l)γ=30γ; z 2=29(6-l)γ=145γ; z 2'=1(6+29)γ=3 5γ; z 3=6(6+29)γ=210γ. При γ = 1 числа зубьев равны z 1=30; z 2=145; z 2'=35; z 3=210. Условие сборки при k = 3: Сопоставляя рассмотренные числовые варианты, приходим к выводу, что первый вариант имеет меньшую сумму (или разность) чисел зубьев в каждой ступени по сравнению со вторым вариантом: 1) z 1 + z 2 = z 3 – z 2' = 20 + l 16 = 170 – 34 = 136; 2) z 1 + z 2 = z 3 – z 2' = 30 + 145 = 210 – 35 = 175. Однако первый вариант не может быть реализован из-за невыполнения условия соседства между смежными сателлитами. Задача. Подобрать числа зубьев планетарного механизма по схеме 2 Решение. Передаточное отношение
Таким образом, Варианты разложения на сомножители будут:
Рассмотрим первый вариант при C 1= l, C 2 = 2, С 2' = 1, С 3 = 7. z 1= γ(С 3- С 2') С 1 = 6γ, z 2’=γ (C 1+ C 2) C 2'= 3γ, z 2= C 2(С з- С 2') γ = 12γ, z 3= C 3(C 1+ C 2) γ = 21γ. Поделив выражение на 3, имеем: z 1=2γ; z 2=4γ; z 2'=γ; z 3=7γ. Наименьшее колесо 2', а число его зубьев должно быть >17. Принимаем z 2' = 19, тогда γ = 19 и z 1 = 2·19 = 38; z 2 = 4·19 = 76; z 3 =7·19 = 133. Определяем возможное число блоков сателлитов по внешнему зацеплению:
Выбираем k = 4 и проверяем условие сборки:
Условие сборки не удовлетворяется, поэтому принимаем k = 3 и снова проверяем условие сборки: l =190. Условие сборки обеспечивается при k = 3. Пример подбора чисел зубьев колес двухрядного планетарного механизма с двумя внешними зацеплениями
Этот механизм представляет собой редуктор Давида по схеме 3 (рис. 4.13). Передаточное отношение В первом случае будет неравенство Для этого механизма условие соосности имеет выражение: (z 1+ z 2) m 1=(z 2'+ z 3)· m 2. Условие сборки: Максимальное число сателлитов из условия соседства:
Решение задачи подбора чисел зубьев механизма z 1, z 2, z 2', z 3 возможно в неопределенном числе вариантов, так как при четырех неизвестных имеем два уравнения (уравнение Виллиса и условие соосности). Воспользуемся методами, рассмотренными подробно для схемы 2. Согласно методу отношений обозначим: Задаваясь значением х, определяем из этого равенства величину Уравнение сборки принимает вид
Принимаем число сателлитов k = 3; 4; 5; 6 и т.д., а числа зубьев на каждом из них - в пределах от 150 до 18. Подставив значения k и z в формулы, получаем предельные значения х и у, удовлетворяющие условиям соседства:
Наибольшая величина передаточного отношения для одной зубчатой пары При подборе чисел зубьев редуктора по схеме 3 задаемся параметром х, ограничивая его величину предельными значениями:
Если х > 1 и у > 1, то при числе сателлитов k = 3,4,5 условия соседства всегда удовлетворяются. Задачу подбора чисел зубьев этого редуктора следует выполнять в следующем порядке: · подбирают значения параметра х, определяя его нижний предел при возможно наибольшем числе саттелитов; · определив по формуле · составляют уравнение z 3 + z 2' = (x + l) z 2, из которого определяют коэффициент пропорциональности, и затем – числа зубьев колес 1, 2, 2', 3; · расчет заканчивают проверкой по уравнению соседства Если вместо
Подобрав числа зубьев редуктора и зная угловую скорость ω Н водила Н, можно определить угловую скорость ω2 = ω2' сателлитов 2 и 2'. Так как скорость VА точки А водила и скорость центров сателлитов равны, а точка С является мгновенным центром вращения колеса 2', можно записать
откуда определяют величину ω2'. Задача. Подобрать числа зубьев редуктора, если дано: Решение. Так как Принимаем: а)
откуда z 2 = 20 a, a = l; 2; 3; 4... Принимаем а = 2, тогда будем иметь z 2 = 40: z 1 = x·z 2 = 15; z 2'=16; z 3 = 72.
|

 , где m – модуль зубчатого колеса.
, где m – модуль зубчатого колеса.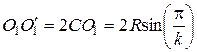 , где R – радиус окружности, на которой располагаются центры сателлитов; k – число сателлитов.
, где R – радиус окружности, на которой располагаются центры сателлитов; k – число сателлитов.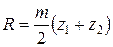 .
.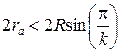 или
или 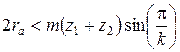 .
. , где ha * – коэффициент высоты головки зуба. Следовательно:
, где ha * – коэффициент высоты головки зуба. Следовательно: 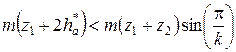 или
или  .
.
 .
.

 ;
; – для внутреннего зацепления;
– для внутреннего зацепления;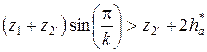 – для внешнего зацепления.
– для внешнего зацепления.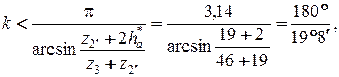
 , то на линии OI вновь расположится ось симметрии впадины колеса 1. Если сателлиты располагаются в параллельных плоскостях, то после поворота колеса 1 на угол τ1 можно установить второй сателлит. При повороте колеса 1 на угол τ1 водило должно повернуться на угол τн:
, то на линии OI вновь расположится ось симметрии впадины колеса 1. Если сателлиты располагаются в параллельных плоскостях, то после поворота колеса 1 на угол τ1 можно установить второй сателлит. При повороте колеса 1 на угол τ1 водило должно повернуться на угол τн:
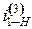 – передаточное отношение при условии, что колесо 1 – ведущее звено, а колесо 3 – неподвижное. Очевидно, что максимальное число сателлитов
– передаточное отношение при условии, что колесо 1 – ведущее звено, а колесо 3 – неподвижное. Очевидно, что максимальное число сателлитов 
 получим
получим 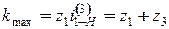 .
. . Для разгрузки центральныхподшипников и возможности передачи большей мощности в планетарных редукторах устанавливается несколько симметрично расположенных сателлитов. Число k сателлитов обычно колеблется в пределах от 2 до 12, иногда больше; в машиностроении чаще всего применяют передачи с числом k = 3–6.
. Для разгрузки центральныхподшипников и возможности передачи большей мощности в планетарных редукторах устанавливается несколько симметрично расположенных сателлитов. Число k сателлитов обычно колеблется в пределах от 2 до 12, иногда больше; в машиностроении чаще всего применяют передачи с числом k = 3–6. ,не более
,не более
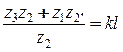 ;
;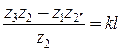 .
. где D – общий наибольший делитель чисел z1 и z2¢.
где D – общий наибольший делитель чисел z1 и z2¢. ,
,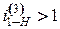 , то передача этого типа при ведущем звене 1 служит для уменьшения скорости вращения ведомого звена – водила Н, а при ведущим звене Н – для увеличения скорости вращения ведомого колеса 1.
, то передача этого типа при ведущем звене 1 служит для уменьшения скорости вращения ведомого звена – водила Н, а при ведущим звене Н – для увеличения скорости вращения ведомого колеса 1.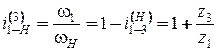 ;
; ;
;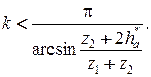
 , которое подставляем в уравнение соосности:
, которое подставляем в уравнение соосности:
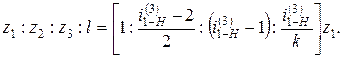
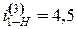 ; m = 10 мм; ha * =1.
; m = 10 мм; ha * =1.

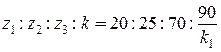 ,
,
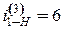 при числе сателлитов k = 3 и h*a = 1.
при числе сателлитов k = 3 и h*a = 1.
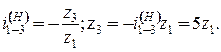 Принимаем z 1=20, тогда z 3=5 · 20=100. Из условия соосности z 3 = z 1+2 z 2. Определяем
Принимаем z 1=20, тогда z 3=5 · 20=100. Из условия соосности z 3 = z 1+2 z 2. Определяем 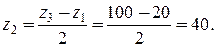
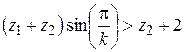 ;
;
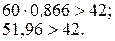
 .
. .Редуктор должен быть соосным.
.Редуктор должен быть соосным. , то размеры редуктора со сдвоенными сателлитами (3-я схема) будут недопустимо большими. Редуктор Давида (4-я схема) из-за низкого КПД можно использовать только в несиловых передачах. Следовательно, проектируемый редуктор должен быть многоступенчатым. При двух ступенях среднее передаточное отношение каждой ступени
, то размеры редуктора со сдвоенными сателлитами (3-я схема) будут недопустимо большими. Редуктор Давида (4-я схема) из-за низкого КПД можно использовать только в несиловых передачах. Следовательно, проектируемый редуктор должен быть многоступенчатым. При двух ступенях среднее передаточное отношение каждой ступени 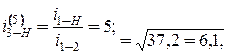 , и их можно выполнить планетарными типа Джемса (рис. 4.16, б).
, и их можно выполнить планетарными типа Джемса (рис. 4.16, б).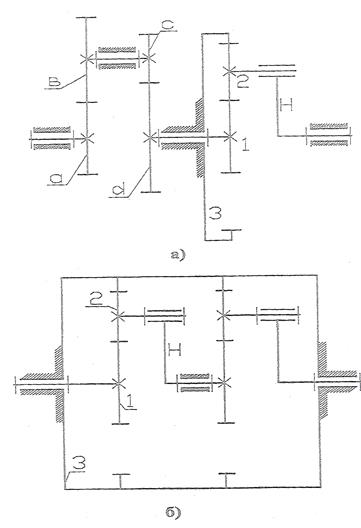
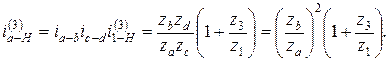
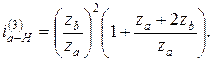
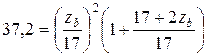 .
.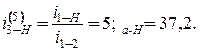
 ;
; 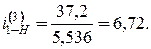
 .
.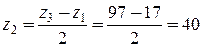 .
. . Если же принять z 1=18,
. Если же принять z 1=18, 
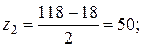
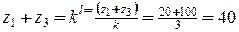 ;
; 
 .
.

 .
. .
. .
. ,
, .
. всегда положительно, поэтому колесо 1 и водило Н вращаются в одном направлении. На основании ранее изложенного для этого механизма передаточное отношение равно:
всегда положительно, поэтому колесо 1 и водило Н вращаются в одном направлении. На основании ранее изложенного для этого механизма передаточное отношение равно: .
.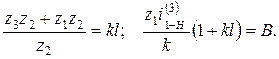
 при
при  ;
; при
при  .
.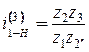 , с учетом, что из условия соосности при m 1= m 2 и
, с учетом, что из условия соосности при m 1= m 2 и  , вычисляется как
, вычисляется как 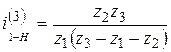 .
.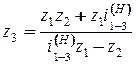 . Это выражение дифференцируем по z 1:
. Это выражение дифференцируем по z 1: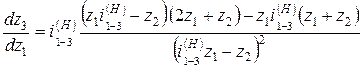 .
. , получаем z lmin=18 – 26.
, получаем z lmin=18 – 26. .
. и z 2 возможно только при условии z 1= z 2' = z min. Тогда условие соосности при одинаковом модуле колес будет z 1+ z 2= z 3- z 1 или z 3=2 z 1+z2.
и z 2 возможно только при условии z 1= z 2' = z min. Тогда условие соосности при одинаковом модуле колес будет z 1+ z 2= z 3- z 1 или z 3=2 z 1+z2.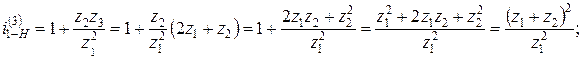
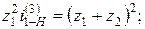
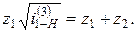
 .
. . Тогда
. Тогда
 .
.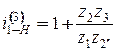 находится значение
находится значение  – несократимая дробь. Простые числа М и N представляются в виде сомножителей
– несократимая дробь. Простые числа М и N представляются в виде сомножителей 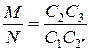 , каждый из которых пропорционален числам зубьев. Полагая С 2/ C 1 пропорциональным z2/z1, получаем z 2= z 1(C 2/ C 1), а С 3/ С 2' пропорциональным z 3/ z 2', имеем z 3= z 2’(C 3/ C 2’). Подставляя эти значения в условие соосности при m 1= m 2 z 1+ z 2= z 3- z 2', получаем z 1+ z 1(C 2/ C 1)= z 2'(C 3/ C 2’)- z 2’ или z1[(C 1+ C 2)- C 2']=z2'[(C 3- C 2')- C 1]. Чтобы это соотношение было тождественно, проще всего положить, что z 1=(C 3- C 2') C 1, z 2'=(C 1+ C 2) C 2'. Аналогичные рассуждения дают z 2= C 2(C 3- C 2'), z 3= C 3(C 1+ C 2). Чтобы выполнялось условие правильного зацепления, вводится множитель γ (любое положительное число). Тогда окончательно имеем для этой схемы:
, каждый из которых пропорционален числам зубьев. Полагая С 2/ C 1 пропорциональным z2/z1, получаем z 2= z 1(C 2/ C 1), а С 3/ С 2' пропорциональным z 3/ z 2', имеем z 3= z 2’(C 3/ C 2’). Подставляя эти значения в условие соосности при m 1= m 2 z 1+ z 2= z 3- z 2', получаем z 1+ z 1(C 2/ C 1)= z 2'(C 3/ C 2’)- z 2’ или z1[(C 1+ C 2)- C 2']=z2'[(C 3- C 2')- C 1]. Чтобы это соотношение было тождественно, проще всего положить, что z 1=(C 3- C 2') C 1, z 2'=(C 1+ C 2) C 2'. Аналогичные рассуждения дают z 2= C 2(C 3- C 2'), z 3= C 3(C 1+ C 2). Чтобы выполнялось условие правильного зацепления, вводится множитель γ (любое положительное число). Тогда окончательно имеем для этой схемы:  =29 и варианты разложения на сомножители будут:
=29 и варианты разложения на сомножители будут: и т.д.
и т.д. , т.е. C 2/ C 1=29/5 и С 3/ С 2'=5/1 или C 2/ C 1=29/6 и С 3/ С 2'=6/1. Это обусловливается тем, что для данной схемы минимальные габариты механизма соответствуют передачам, колеса которых имеют наибольшую разность диаметров колес z 2 и z 2' на сателлите.
, т.е. C 2/ C 1=29/5 и С 3/ С 2'=5/1 или C 2/ C 1=29/6 и С 3/ С 2'=6/1. Это обусловливается тем, что для данной схемы минимальные габариты механизма соответствуют передачам, колеса которых имеют наибольшую разность диаметров колес z 2 и z 2' на сателлите.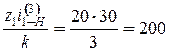 – целое число, т.е. передача собирается без натягов.
– целое число, т.е. передача собирается без натягов. при
при 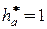 ,
,
 – целое число, т.е. передача собирается без натягов. Условие соседства выполняется, так как
– целое число, т.е. передача собирается без натягов. Условие соседства выполняется, так как  .
. =15. Модуль колес одинаков,
=15. Модуль колес одинаков, 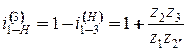 .
. .
. .
.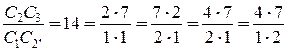 и т.д.
и т.д.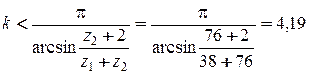 .
.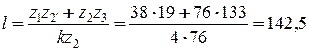 .
.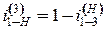 механизма, в зависимости от числового значения
механизма, в зависимости от числового значения  может быть, согласно формуле Виллиса, и положительным, и отрицательным, т.е. водило Н и колесо 1 могут вращаться либо в одном и том же, либо в противоположном направлении.
может быть, согласно формуле Виллиса, и положительным, и отрицательным, т.е. водило Н и колесо 1 могут вращаться либо в одном и том же, либо в противоположном направлении. и при ведущем колесе 1 передача является ускоряющей, т.е. ведомое звено Н вращается с большей угловой скоростью, чем ведущее колесо 1. Во втором случае наблюдается неравенство
и при ведущем колесе 1 передача является ускоряющей, т.е. ведомое звено Н вращается с большей угловой скоростью, чем ведущее колесо 1. Во втором случае наблюдается неравенство  , т.е. абсолютная величина
, т.е. абсолютная величина 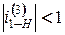 ,так и замедляющей при
,так и замедляющей при  .
.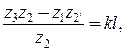
 .
. при
при  ;
; при
при  .
. . Тогда уравнение соосности запишется так: (z 1+ z 2) q = z 3+ z 2'= (x +l) z 2 q. Отношение:
. Тогда уравнение соосности запишется так: (z 1+ z 2) q = z 3+ z 2'= (x +l) z 2 q. Отношение: 
 .
. , а условия соседства будут:
, а условия соседства будут: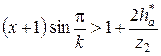 ;
;  .
. , где еk в зависимости от числа k сателлитов принимает следующие значения:
, где еk в зависимости от числа k сателлитов принимает следующие значения: и т.д.
и т.д. зависит от числа зубьев z ( n -1) меньшего сопряженного колеса.
зависит от числа зубьев z ( n -1) меньшего сопряженного колеса.

 значение
значение  из уравнения сборки
из уравнения сборки 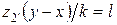 , находят величины, пропорциональные количествам z 2' зубьев сателлита 2' и
, находят величины, пропорциональные количествам z 2' зубьев сателлита 2' и  центрального колеса 3;
центрального колеса 3;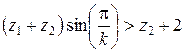 найденного числа зубьев и по формуле
найденного числа зубьев и по формуле  , т.е. ведущим звеном является водило Н, то задачу решают аналогично рассмотренной в соответствии с формулой
, т.е. ведущим звеном является водило Н, то задачу решают аналогично рассмотренной в соответствии с формулой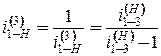 .
.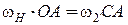 или
или  ,
,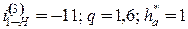 (рис. 4.13, схема 2).
(рис. 4.13, схема 2).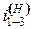 =12, то величина х должна быть меньше 1. Число 12=2·2·3,
=12, то величина х должна быть меньше 1. Число 12=2·2·3,  , то можно предварительно задаться величинами
, то можно предварительно задаться величинами  и др.
и др.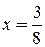 , находим
, находим 
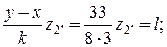
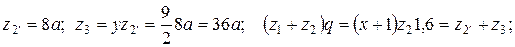
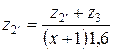 или
или 



