Система двох дискретних випадкових величин.На одному й тому самому просторі елементарних подій W можна визначити не одну, а кілька випадкових величин. Така потреба постає, наприклад, коли досліджуваний об’єкт характеризується кількома випадковими параметрами. Сукупність випадкових величин Одночасна поява внаслідок проведення експерименту n випадкових величин (X1, X2, …, Xn) з певною ймовірністю являє собою n-вимірну випадкову величину, яку називають також системою n випадкових величин, або n-вимірним випадковим вектором. _________________________________
31. Закон розподілу ймовірностей дискретної двомірної величини. Законом розподілу двох дискретних випадкових величин називають перелік можливих значень Y = yi , X = xj та відповідних їм імовірностей спільної появи. У табличній формі цей закон має такий вигляд:
Тут використано такі позначення
Умова нормування має такий вигляд:
_________________________________
32. Коефіцієнт кореляції та його властивості. Під час вивчення системи двох і більше випадкових величин доводиться з’ясовувати наявність зв’язку між цими величинами та його характер. З відповідною метою застосовують так званий кореляційний момент:
У разі Κху = 0 зв’язок між величинами Х та Y відсутній. Тісноту кореляційного зв’язку характеризує коефіцієнт кореляції:
Якщо випадкові величини Х та Y є незалежними, то Κху = 0 і rху = 0. Рівність нулеві rху є необхідною, але не достатньою умовою незалежності випадкових величин. Дві випадкові величини Х і Y називають некорельованими, якщо rху = 0, і корельованими, якщо rху ¹ 0. _________________________________
33. Функція розподілу ймовірностей системи двох випадкових величин та її властивості. Функцією розподілу ймовірностей системи двох випадкових величин (Х, Y) називають таку функцію двох аргументів х, у, яка визначає ймовірність спільної появи подій (X < x) I (Y < y): F(x,y) = P((X < x) I (Y < y)). Властивості F(x, y) 1. 0 £ F(x, y) £ 1, оскільки 0 £ P((X < x) I (y < y)) £ 1. 2. Якщо один із аргументів F(x, y) прямує до +
3. 4. 5. F(x, y) є неспадною функцією аргументів х і у. Р(а < Х < b, Y < y) = F(b, y) – F(a, y); P(X < x, c < Y < d) = F(x, d) – F(x, c). 6. Імовірність влучення точки (Х, Y) в довільний прямокутник (a < X< b, c < Y < d) обчислюємо так: P(a < x < b, c < y < d) = F(b, d) + F(a, c) – F(a, d) – F(b, c). _________________________________
34. Щільність розподілу двомірної випадкової величини. Характеристикою системи неперервних випадкових величин є щільність імовірностей.
Функція f (x, y) може існувати лише за умови, що F (x, y) є неперервною за аргументами х і у та двічі диференційовною. Властивості f (x, y) 1. Функція f (x, y) ³ 0, оскільки F(x, y) є неспадною відносно аргументів х і у. 2. Умова нормування системи двох неперервних випадкових величин (Х, Y) така:
3. Імовірність розміщення системи змінних (х, у) в області
4. Функція розподілу ймовірностей системи двох змінних визначається з рівняння
5. Якщо
_________________________________ 35. Основні числові характеристики системи двох неперервних випадкових величин (Х,У).
_________________________________ 36. Ймовірність влучення випадкових точок у прямокутник. Імовірність влучення точки (Х, Y) в довільний прямокутник (a < X< b, c < Y < d) обчислюємо так: P(a < x < b, c < y < d) = F(b, d) + F(a, c) – F(a, d) – F(b, c). Доведення. Розглянемо такі випадкові події: A = (X < b, Y < d); B = (X < a, Y < c); C = (a < X < b, Y < c); D = (X < a, c < Y < d); E = (a < X < b, c < Y < d). Оскільки випадкові події B, C, D, E несумісні, маємо: A = B U C U D U E. P(A) = P(B U C U D U E) = P(B) + P(C) + P(D) + P(E). P(x < b, y < d) = P(x < a, y < c) + P(a < x < b, y < c) + P(х < a, c < у < d) + P(a < x < b, c < y < d). F(b, d) = F(a, c) + F(b, c) – F(a, c) + F(a, d) – F(a, c) + P(a<X<b,c<Y<d); P(a<X<b,c<Y<d)=F(b,d)+F(a,c)–F(a, d) – F(b, c), що й треба було довести. _________________________________ 37. Функція 1-ого випадкового аргументу. Функцією випадкового аргументу Х називають таку випадкову величину Y, яка набуває значення Y = у = Коли Х є неперервною випадковою величиною, то і Y = 1) Нехай закон дискретної випадкової величини Х задано таблицею:
Тоді закон розподілу випадкової величини Y =
Умова нормування для f (у):
За знайденою f (у) функцією розподілу ймовірностей визначається
_________________________________ 38. Математичне сподівання функції 1-ого випадкового аргументу. Функцією випадкового аргументу Х називають таку випадкову величину Y, яка набуває значення Y = у = Коли Х є неперервною випадковою величиною, то і Y = Математичне сподівання дискретного випадкового аргументу
Математичне сподівання функцій неперервного випадкового аргументу:
_________________________________
39. Функції 2-х випадкових аргументів. У загальному випадку функцію двох аргументів Х і Y можна позначити як
де Якщо Х та Y є дискретними випадковими величинами, то і Z буде дискретною. Якщо Х та Y є неперервними, то і Z буде неперервною.
_________________________________
40. Математичне сподівання суми двох випадкових аргументів. Математичне сподівання. М (Х + Y) = М (Х) + М (Y). (1) Висновок 1. М(АХ+ВY+С)=АМ(Х)+ВМ(Y)+С. А, В, С — деякі сталі. Висновок 2.
_________________________________
41. Біноміальний розподіл. Цілочислова випадкова величина X має біноміальний закон розподілу, якщо ймовірність її можливих значень обчислюється за формулою Бернуллі:
При перевірці виконання умови нормування використовується формула біному Ньютона, тому закон розподілу називають біноміальним:
Імовірнісна твірна функція для біноміального закону
Основні числові характеристики:
_________________________________
42. Закон розподілу неперервної випадкової величини. Рівномірний розподіл. Цілочислова випадкова величина Х має рівномірний закон розподілу, якщо ймовірності її можливих значень обчислюються за формулою:
Імовірнісна твірна функція:
Числові характеристики:
_________________________________
43. Нормальний розподіл. Випадкова величина Х має нормальний закон розподілу ймовірностей, якщо f (х) = де а = М (X), s = s (X). Отже, нормальний закон визначається звідси параметрами а і s і називається загальним. Тоді F(x)=
Для нормального закону Мо=Ме=а. Загальний нормальний закон позначають: N (a; s). _________________________________
|

 які розглядаються спільно, називається системою
які розглядаються спільно, називається системою  випадкових величин. Якщо
випадкових величин. Якщо  тобто розглядається система двох випадкових величин
тобто розглядається система двох випадкових величин  , то геометрично її можна тлумачити як випадкову точку з координатами
, то геометрично її можна тлумачити як випадкову точку з координатами 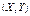 на площині
на площині 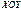 або як випадковий вектор, складові якого — випадкові величини
або як випадковий вектор, складові якого — випадкові величини 
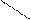 X=xj
Y=yi
X=xj
Y=yi
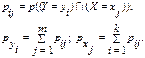
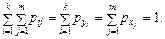

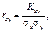
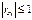 , або
, або  .
. , то функція розподілу системи прямує до функції розподілу одного аргументу, що не прямує до +
, то функція розподілу системи прямує до функції розподілу одного аргументу, що не прямує до + 

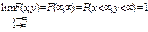

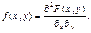
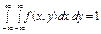 .
. обчислюється так:
обчислюється так:
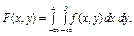
 , то
, то
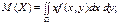
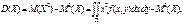




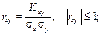
 (х) щоразу, коли Х = х, де
(х) щоразу, коли Х = х, де 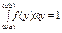 .
. .
.
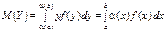 ;
;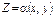 ,
, є невипадковою функцією.
є невипадковою функцією.

 .
.
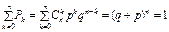 .
. .
.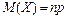 .
.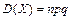 ;
; .
. . (1)
. (1)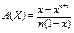 .
. .
.

 ,
,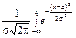 dx. (2)
dx. (2)


