ПРИЛОЖЕНИЕ Г. Биномиальное распределение, распределения Пуассона и ГауссаОбозначим биномиальное распределение (5.8) как
и найдем ее первую и вторую производные по параметру z в точке z = 1:
Согласно определению среднего,
Тогда, в силу (Г.1)
Чтобы найти дисперсию биномиального распределения, разложим выражение для квадрата отклонения случайной величины от среднего:
Можно видеть, что при усреднении второго слагаемого в этом выражении получается нуль, так как среднее отклонение от среднего равно нулю. Далее представим первое слагаемое в следующем виде:
Используя определение дисперсии, найдем, что
Далее воспользуемся тем, что, согласно (Г.2), среднее значение произведения n (n – 1) есть вторая производная функции g (z). Отсюда
Тогда
При
Осуществим предельный переход
Аналогично, пользуясь определением второго замечательного предела
получаем для третьего множителя
Таким образом,
Полученное распределение WP (n) известно как распределение Пуассона. Преобразуем соответствующим образом распределение Пуассона для Тогда
Во-вторых, используем тот факт, что распределение WР (n) заметно отлично от нуля лишь в довольно узкой области справа и слева от максимума (см. рис. 5.2). Тогда, раскладывая показатель экспоненты в (Г.3) в ряд Тейлора по
с точностью до первого неисчезающего члена (в данном случае – второго порядка по Δ n) и заменяя под корнем 2 πn на 2 π;
Выражение (5.14) представляет собой не что иное, как закон Гаусса, или нормальное распределение непрерывной случайной величины.[207]
|

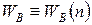 и вычислим для него среднее число ядер
и вычислим для него среднее число ядер 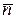 , распадающихся за некоторый промежуток времени. Для этого введем функцию
, распадающихся за некоторый промежуток времени. Для этого введем функцию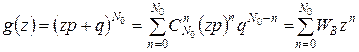
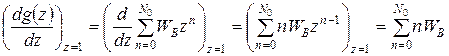 , (Г.1)
, (Г.1)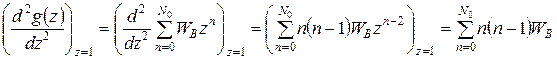 . (Г.2)
. (Г.2)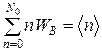 .
.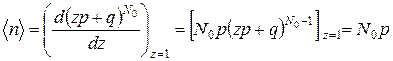 . (5.10)
. (5.10)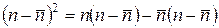 .
.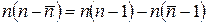 .
.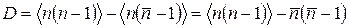 .
.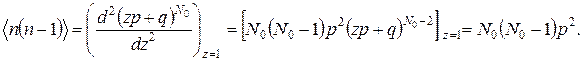
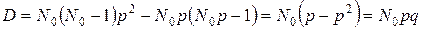 . (5.11)
. (5.11) и р << 1 выражение (5.8) можно упростить. Подставляя, согласно (5.10),
и р << 1 выражение (5.8) можно упростить. Подставляя, согласно (5.10), 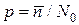 получаем:
получаем: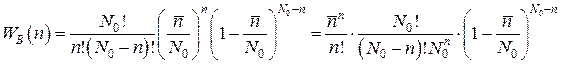 .
. во втором множителе:
во втором множителе: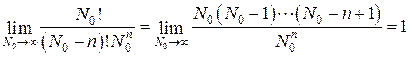 .
.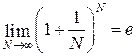 ,
,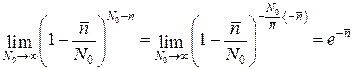 .
.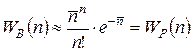 . (5.12)
. (5.12)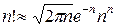 .
.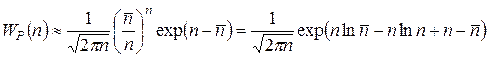 . (Г.3)
. (Г.3)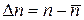 ,
,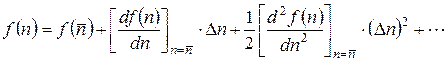 ,
,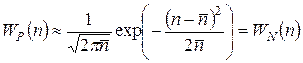 . (5.14)
. (5.14)


