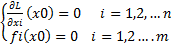III. Функции нескольких переменныхМетрическое пространство называется совокупность объектов таких что для любых х,у определено правило p(x,y) 1.p(x,x)=0 2.p(x,y)=p(y,x) 3.p(x,z)≤p(x,y)+p(y,z) p-метрика _____________________________________________________________ G ⊂ M-открытое если для любого х пренадлежащего G существует дельта такая что Sхб ⊂ G в натуральных точках множества F ⊆ М –замкнутое ó
Опр. т. Х0 = UL-открытое множество (М), L ∈ A A={1,2,3….n} {UL}^(n)={U1,U2,U3,….,Un} A={[0,1]} {UL}L ∈[0,1] Множество называется покрытием множества А, если А с ULUL Покрытие называется конечным если семейство множества А конечно Теорема1. Если А конечно=> А-ограничено Док-во. Для любого х ∈А ∃ Sхб: x= Sхб => ∃ x1,x2,x3…..xn A ⊂ Sх1б U Sх2б U….U Sхnб чтд. Теорема2. Если А-компактно=> A –замкнуто Док-во: Х0-предельная точка множества А, х0 ∉А x∈A Sх0б1 бi<(p(x,x,0))/2 для каждой точки х∈А построим окрестность Sхб чтд. Теорема3. Если множество А компактно => ∀ B⊂A B-бесконечно ∃ xo-предельная точка ∈B,x0∈A Док-во. Х-предельная точка для В, х ∉А Sх0б => ∃ x∈B,x≠x0 противоречие. Ограниченность и замкнутость –необходимые условия замкнутости. Отоброжением Rn->Rm называется правило которое переводит f(x) из Rn B Rm 1)n=m=1 f:R-->R y=f(x) 2)n,m=1 f:RnàR y=f(x)=f(x1,x2,x3….xn) 3)n=1,m f:RàRm y=( Предел функции в точке f:RnàRm x0∈ Rn
Лемма. 1)
2)n,m=1 y=f(x1,x2,….,xn)
∃ Свойства пределов 1)однородность
2)аддитивность
Непрерывность отоброжения Y=f(x) RnàRm x0∈D(f) f(x)-непрерывна в т. х0,если ∃ Опр.направлением в пространстве Rn назовём совокупность векторов коллинеарных S Опр. сечением функции y=f(x) в т. х0 в направлении вектора S называется функция одной переменной. Y=f(x0+tS)=𝛗(s) Теорема. Если функция f(x) непрерывна в т. х0=> все её сечения для любого S непрерывна в т. t=0 𝛗s(t)=f(x0+tS) (ОБРАТНОЕ НЕВЕРНО) Т.Вейерштрасса. Пусть f(x):RnàR D(f)-замкнута и ограничена а функция f непрерывна ∃ xn ∈D(f) f(xn)≤f(x) ∀x ∈ D ∃ xm ∈D(f) f(xm)≥f(x) ∀x ∈ D Зам(о связности) D-связно,f-непр на D=>f(D)-связное f:RnàR f∈R D-компакт M-max f m-min f f:RnàR y=f(x)=f(x1,x2,x3,….,xn) x0(x01,x02) △x=( △f=f(x0+△x)-f(x0) F(x) диференц. в т. х0 если △f=f(x0+△x)-f(x0) =(а1+△х)+α(△х)
Опр. Линейн. Относ. △х част. приращение функции называется дифференциал функции df(x0)=a1* △х1+ a2*△х2+…+an*△хn= опр. Сечение f(x) в направлении y=x12+x22 S=(?) x0=(0,0) сечение называется координатным если в качестве вектора S выбран…? Опр. y=f(x),x0 S-напр. |S|=1 𝛗(t)=f(x0+ts) Fs`(x0)=𝛗`(0)= S=ei fi`(x0)-частная производная ei= (
f1`(x0)= опр. fs`(x0)
{ T. ∀ S
Т.(достаточное условие существования производ., ∀ S) y=f(x),x∈ Sx0 , ∃df(x0), |S|=1 ∃ Док-во:
S=ei ∃ F(x0+tei)-f(x0)=Ai*t+α Опр. f `(x0)-градиент функции f(x)
Существование частной производной Y=f(x) ∃ dm f(x), x=x0 ð ∃ = Зам1. Если функция непрерывна то существует диффиренциал n-го порядка Экстремальные св-ва градиентов Направл. S∈Rn (|S|=1) называется экстремальным если производная от функции Т. об экстремальном св-ве градиента grad max док-во:
|V|=|gradf|=sqrt( Следствие. Наибольшая скорость изменения функции в данной точке это |grad f| Сложн. Ф нескольких переменных (суперпозиция) y=y(x(t)) RnàR T.(о непрерывности сложного отобр.) Если х=х(t)-непр. в т. х0 и y(x) непр. в т. х0 => y(x(t))-непр. в т. t0 Дифференц. Сложного отобр. x=х(t) ∃ d x(t0) y=y(x) ∃ dy(x0) x0=x(t0) 1) ∃ dy(x(t)) 2) Jy=yT(x0)*Jx(t0) следовательно ∃ dy(x(t))=yT(x0)*Jx(t0)dt dy(x(t))=yT(x0)*x`(t0)dt правило нахождения производной сложной функции
Функции нескольких переменных заданных неявно z=f(x,y) f(x0,y0)=0 f(x,y)=0 опр. f(x,y)=0 не явн. Обр. задаёт ф. у(х) в окрестности точки х0,если 1) ∀x∈ Sхб ∃! У: f(x,y)=0 =>y0=y(x0) f(x0,y0)=0 Теорема (о существ. и диф. Функции заданной неявно отобр.) S(х0,y0)б f(x0,y0)=0 ∃ ð 1)f(x,y)=0 => y=y(x) y(x0)=y0 ð 2)если ф. ∃df(x0,y0)=> ∃ y`(x)= Зам.(о формуле диференц. неявной функции) F(x,y)=0 y=y(x) f(x,y(x))≡0, для любого х из окрестности точки х0
y`(x0)= неявные отображения 𝛗(x,y)=0 => 𝛗1(x1 xy,..,xn,y1,y2,…,yn)=0 𝛗m(x1,x2...xm, y1,y2,…,ym)=0 => yj=y1(x1,..,xn),j={1,2,…,n}
x=
y=y(x)=
y=y(x) y`(x0)=J=( dy=y`(xo)dx
J=
Т.(о неявн. Отобр) x ∈Rn y∈Rm 𝛗=𝛗(x,y):Rn+màRm
пусть выпл. условия: 1)𝛗(x0,y0)=не ноль 2) ∃ d𝛗(xn,ym) 3)| => ∃ опр.(x0,y0) 1. ∀x ∃! y: 𝛗(x,y)=0=> y=y(x) 2. ∃ dy=>
экстремумы y=f(x) x∈Rn, D⊂Rn опр. x0-внутр. т D=>∃ окрестность точки х0 ⊂D x0∈D Пусть
опр.x0∈D, x0=argminf(x) если f(x0)≤f(x) ∀x∈D x0=argminf(x) x0-внутр f(x0)≤f(x) х∈ Sх0б т. Вейерштрасса y=f(x) x∈D D-замкнут и ограниченная ð ∃ xm: f(xm)≤f(x) xm∈D ð ∃ xn: f(xn)≥f(x) xn∈D Необходимое условие экстр. Т.ферма x0=arglocextr f(x) ∃df(x0)=>df(x0)≡0(∀△x) док-во 𝛗(t)=f(x0+t△x) x0=arglocextr f(x) ð t=0 0=argloc 𝛗(t)=> 𝛗`(0)=0=df(x0) x0=arglocextr f(x) => grad f(x0)=0
необходимые условия экстремума 2 порядка
x0=arglocextr f(x), d2f(x0)=> d2f(x0)>0 min ∀△x d2f(x0)<0 max ∀△x док-во 1. функция Лагранжа 𝛗(t)=f(x0+t△x) 𝛗`(0)=0 𝛗``(0)>0 min 𝛗```(0)<0 max
H(x0)=(
2. если d2f(x0) d2f(x0)=(△x)TH*△x= если x0=arglocmin f(x)=> H(x0)>0 если x0=arglocmax f(x)=> H(x0)<0
Критерий Сильвестра H>0 ó Mi>0 i=1,2….n d2f(x0)=(△x)TH(△x)=(H△x,△x)>0, ∀△x достаточное условие экстремума
Т. Пусть y=f(x) опред. x∈ Sх0б,x0-внутр т. обл опред ∃ d2f(x0)
1)f `(x0)=0 2)f ``(x0)> 0 или f ``(x0)<0 x0-argmin x0-argmax
док-во: 𝛗(t)= f(x0+t△x) 𝛗(t)= 𝛗(0)+ 𝛗(0)=f(x0) 𝛗 `(0)=df(x0) 𝛗 ``(0)=d2f(x0)
𝛗(t)= 𝛗(0)+ 𝛗(t)- 𝛗(0)= экстремумы функции нескольких переменных при наличии ограничений y=f(x) x∈D, x∈µ-огранич.
D-замкнут и огранич
2)З. с огр. равенствами
Необх. условия в з. с огр. равенствами
опр. функцией Лагранжа ассоциированной задачей огран. равенствам назыв. ф.
β0-число β=
dim x=n F(x)=0
Принцип множителей Лагранжа
∃ df, dF(x), x0=argextr f(x) => ∃0,β∈Rm, x0=stat L(x) ó
док-во: пусть n=2 z=z(x,y) z(x,y)àextr f1(x,y)=0
Если x0=argextrf => ð gradz||n ∃ βгрβ:β0gradz0+β*n=0 grad[β0z+β*f1]=0
экстремум с ограничениями неравенствами
Постановка задачи
ограничения на значения вектора x заданы системой неравенств. Предположим, что в точке условного экстремума часть неравенств переходит в равенства, отсортируем g(x), b и λ так, чтобы вторые компоненты отражали строгие равенства g = (g1T g2T)T, b = (b1T b2T)T, λ = (λ1T λ2T)T. Как и прежде, функция Лагранжа в точке экстремума должна быть равна f(x), следовательно в ней (g(x)–b)Tλ = 0. Это означает, что если имеет место неравенствоg1(x) < b1, то λ1 = 0. Для остальных компонент, наоборот, g2(x) – b2 = 0 и λ2 = – dL /db2. Все это вместе можно записать короче
2. Ограничения вида двусторонних неравенств. Постановка задачи
ограничения на значения вектора x заданы двусторонними неравенствами. Функция Лагранжа расширяется
Так как в точке экстремума пребывание и на левой и на правой границе неравенства исключается, соответственные компоненты множителей η и μ никогда не бывают равными нулю одновременно. Вместо двух составляющих можно применить комбинированный множитель λ = η + μ. Знаковые условия разнообразятся, но не более того, точка, подозрительная на условный экстремум, удовлетворяет зависимостям
Условия соблюдения знаковой политики можно объединить в одно
На границах левые или правые множители Лагранжа отличны от нуля и соответствуют частным производным функции L по элементам вектора a или b, внутри разрешимой зоны они нулевые, соответственно, компоненты λ играют роль то левого, то правого отличного от нуля множителя.
|

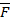 -открытое
-открытое для любого Е>0 существует n0 для любого n>n0 p(xn,x0)<E
для любого Е>0 существует n0 для любого n>n0 p(xn,x0)<E )=
)=  =y(x)
=y(x) =a∈Rn ∀ E>0 ∃б>0 p(x,x0)<б p(f(x),a)<E
=a∈Rn ∀ E>0 ∃б>0 p(x,x0)<б p(f(x),a)<E ó∀ i=1,2,…,n
ó∀ i=1,2,…,n ó∃
ó∃ 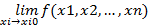
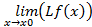 =
= 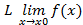
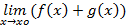 =
= 
 ∀ E>0 ∃ б>0: p(x,x0)<б => p(f(x),f(x0))<E
∀ E>0 ∃ б>0: p(x,x0)<б => p(f(x),f(x0))<E )
) =0
=0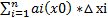 (дифференцируемость неск переем не нашёл)
(дифференцируемость неск переем не нашёл)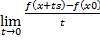
 ) x0ts=
) x0ts= 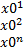
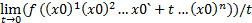
 (x0)=fs`(x0)t, t-приращ. Взятое fs`(x0)=
(x0)=fs`(x0)t, t-приращ. Взятое fs`(x0)= 
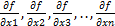 }=f `(x) в точке х0
}=f `(x) в точке х0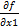 s1+…+
s1+…+  Sn (|S|=1)
Sn (|S|=1) =
= 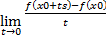 =
= 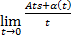 =A*s
=A*s f(x0)-набла f `=grad f(x) в точке х0
f(x0)-набла f `=grad f(x) в точке х0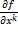 =r≤m x=(x1,x2,…,xm) xi≥0 ∀i
=r≤m x=(x1,x2,…,xm) xi≥0 ∀i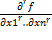

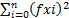 ) чтд.
) чтд.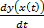 =
= 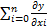 *
* 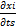
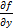 (x0,y0)≠0
(x0,y0)≠0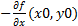
 +
+ 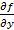 y`(x)=0
y`(x)=0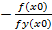
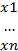 y=
y= 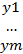
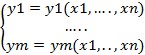
 ) i,j=1,2….m матр Якоби
) i,j=1,2….m матр Якоби
 |≠0
|≠0 =-
=- 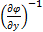 *
* 
 =
= 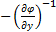 *
* 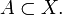 Точка
Точка  называется грани́чной то́чкой мно́жества A, если для любой её окрестности
называется грани́чной то́чкой мно́жества A, если для любой её окрестности 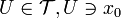 справедливо:
справедливо: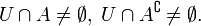
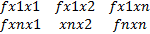 )=
)= 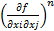 i,j=1 (H(x0)-матр. Гессе)
i,j=1 (H(x0)-матр. Гессе)
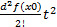 +α(t)
+α(t) +α
+α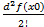 +α, t=0
+α, t=0 ;
;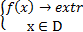 ;
;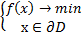 ;
;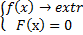 ; F=
; F= 
 -множитель Лагранжа L(x,β0,n)=β0f(x)+
-множитель Лагранжа L(x,β0,n)=β0f(x)+ 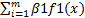
 m<n
m<n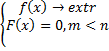
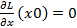
 =>
=> 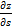 =(gradz,s), |s|=1
=(gradz,s), |s|=1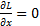 =>
=>