Основных элементарных функцийТаблица 1
Пример 1. Разложить в степенной ряд по степеням Решение. Находим сначала производные заданной функции, затем вычисляем значения функции и ее производных при Ряд Маклорена, для функции Остаточный член формулы Тейлора в форме Лагранжа при Пример 2. Разложить в степенной ряд по степеням Решение. Находим сначала производные заданной функции, затем вычисляем значения функции и ее производных при
Методом математической индукции можно показать, что Ряд Маклорена, соответствующий функции
Он сходится абсолютно для всех значений Остаточный член формулы Тейлора в форме Лагранжа будет иметь вид
Следовательно, Окончательно, согласно теореме о разложении функции в ряд Тейлора, для любого
Продифференцировав этот ряд, можно получить разложение в степенной ряд по степеням Пример 3. Разложить в степенной ряд по степеням Решение. Интегрируя почленно от 0 до Его называют логарифмическим рядом. Этот ряд сходится абсолютно при Если в этом разложении заменить Пример 4. Используя разложение в ряд функции Решение. Обозначим:
Пример 5. Разложить функцию Решение. Используем разложение в ряд функции Приближенное вычисление значений функций. Возможность разложения функции в степенной ряд позволяет существенно упростить многие математические операции: вычисление приближенных значений данной функции, дифференцирование, интегрирование. При приближенном вычислении значения функции сумму ряда заменяют на его частичной суммой: В случае знакочередующегося ряда, члены которого удовлетворяют признаку Лейбница, остаток оценивается по своему первому члену Пример 5. Вычислить приближенное значение Решение. Переведем градусы в радианы
В силу признака Лейбница погрешность не превосходит по абсолютной величине первого из отброшенных членов 0,000003. Пример 6. Вычислить приближенное значение корня Решение. Преобразуем подкоренное выражение и воспользуемся биномиальным рядом № 8 табл. 8.1.
Пример 7. Вычислить приближенное значение корня Решение: Используя разложение
Погрешность этого приближенного равенства определяется суммой членов, следующих после
Заменив, каждый из сомножителей n+2, n+3,….меньшей величиной n+1, получаем:
Значит для нашего случая
Путем подбора определим, при каком значении n будет выполняться неравенство
Применение степенных рядов в приближенных вычислениях определенных интегралов. Пусть требуется вычислить определенный интеграл Пример 7. Вычисление интегрального синуса: Решение. Положив
Находим Полученный ряд можно использовать для вычисления значений Применение степенных рядов к вычислению пределов. Пределы дробей, числители и знаменатели которых стремятся к нулю, можно вычислить с помощью степенных рядов. При этом числитель и знаменатель дроби раскладываются в степенные ряды по степеням одной и той же разности Пример 8. Вычислить Решение. Используя разложения функций
Произведя сокращение на
|




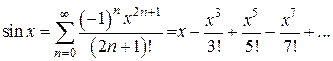
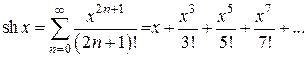

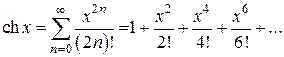
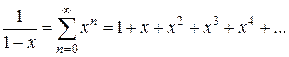

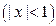
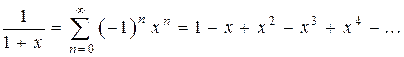
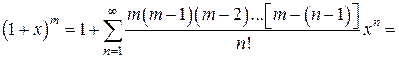
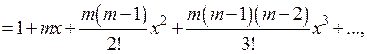


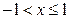
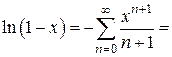

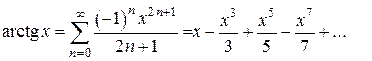
 функцию
функцию 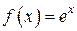 .
.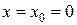 . Имеем
. Имеем  ,
, 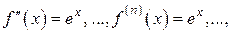
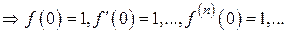
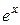 , будет иметь вид
, будет иметь вид  . Он сходится абсолютно для всех значений
. Он сходится абсолютно для всех значений 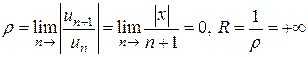 ).
).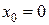 будет иметь вид
будет иметь вид 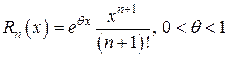 . Ряд
. Ряд 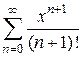 – сходящийся, а потому, в силу необходимого признака сходимости, общий член ряда стремится к нулю, т.е.
– сходящийся, а потому, в силу необходимого признака сходимости, общий член ряда стремится к нулю, т.е. 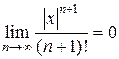 , следовательно,
, следовательно, 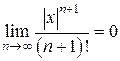 и
и 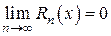
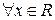 . Таким образом, для любого
. Таким образом, для любого 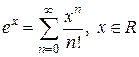 .
. .
.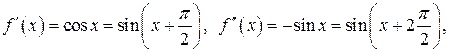

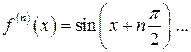
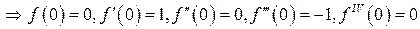 и т.д. (числа 0, 1, 0, –1 будут периодически повторяться).
и т.д. (числа 0, 1, 0, –1 будут периодически повторяться). , будет иметь вид
, будет иметь вид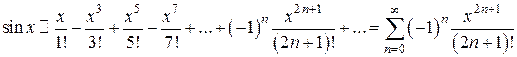 .
.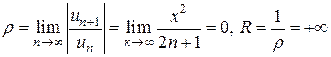 .
.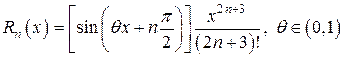 .
.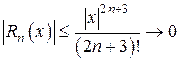 при
при 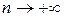 для всякого
для всякого 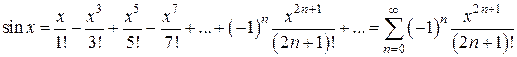 ,
, 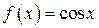 . Это разложение будет иметь вид
. Это разложение будет иметь вид 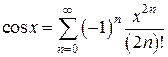 ,
,  .
.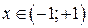 равномерно сходящийся ряд
равномерно сходящийся ряд  получаем ряд Маклорена:
получаем ряд Маклорена: 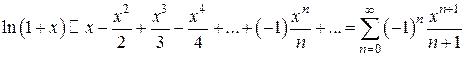 ,
, 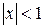 . можно показать, что при
. можно показать, что при 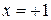 логарифмический ряд сходится условно, а при
логарифмический ряд сходится условно, а при 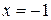 ряд расходится. При этом,
ряд расходится. При этом, 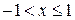 , т.е. имеет место разложение
, т.е. имеет место разложение  .
.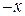 , то получим разложение функции
, то получим разложение функции 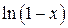 при
при 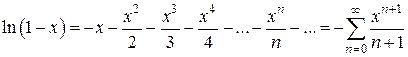 . Вычитая один ряд из другого (первый из второго) и принимая во внимание
. Вычитая один ряд из другого (первый из второго) и принимая во внимание  , находим разложение в степенной ряд функции
, находим разложение в степенной ряд функции 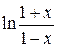 при
при 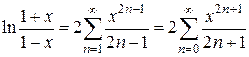 .
. .
.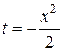 , тогда
, тогда
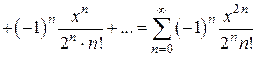 .
. в ряд по степеням х.
в ряд по степеням х.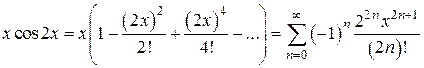 , где
, где 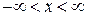 .
.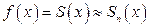 , а остальные члены отбрасывают. Для оценки погрешности найденного приближенного значения нужно оценить сумму отброшенных членов.
, а остальные члены отбрасывают. Для оценки погрешности найденного приближенного значения нужно оценить сумму отброшенных членов. , где
, где  - первый из отброшенных членов ряда. Если ряд знакопостоянный, то ряд, составленный из отброшенных членов, сравнивают с бесконечно убывающей геометрической прогрессией.
- первый из отброшенных членов ряда. Если ряд знакопостоянный, то ряд, составленный из отброшенных членов, сравнивают с бесконечно убывающей геометрической прогрессией.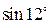 с точностью до 0,001.
с точностью до 0,001. и воспользуемся разложением синуса в степенной ряд
и воспользуемся разложением синуса в степенной ряд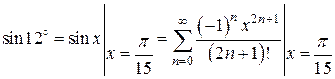
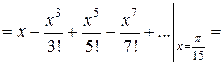
 .
. с точностью до 0,001.
с точностью до 0,001.

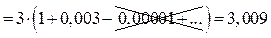 .
.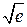 с точностью до 0,00001.
с точностью до 0,00001.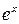 в ряд
в ряд  получаем
получаем .
. в разложении
в разложении 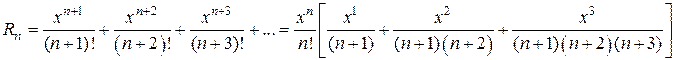
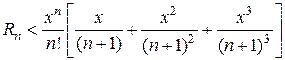 . Получаем бесконечно убавющую геометрическую прогрессию в квадратных скобках:
. Получаем бесконечно убавющую геометрическую прогрессию в квадратных скобках: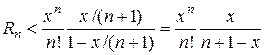
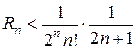
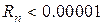 . При n=3 получаем
. При n=3 получаем  , при n=5:
, при n=5: 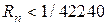 , при n=6:
, при n=6:  , Итак n=6.
, Итак n=6.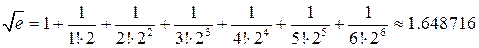
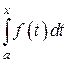 , который или не берется в конечном виде или представляет значительные технические трудности в процессе интегрирования. Разложив
, который или не берется в конечном виде или представляет значительные технические трудности в процессе интегрирования. Разложив 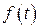 в ряд Маклорена, пользуясь готовыми разложениями функции (табл.1), и почленно проинтегрировав его (при условии, что
в ряд Маклорена, пользуясь готовыми разложениями функции (табл.1), и почленно проинтегрировав его (при условии, что 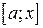 содержится в интервале сходимости), получим
содержится в интервале сходимости), получим 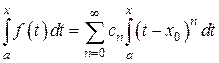 . Полученный ряд можно использовать для вычисления значений
. Полученный ряд можно использовать для вычисления значений 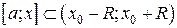 с любой заданной степенью точности.
с любой заданной степенью точности. .
.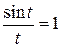 при
при  и приняв во внимание
и приняв во внимание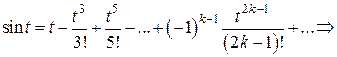
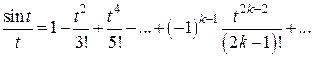
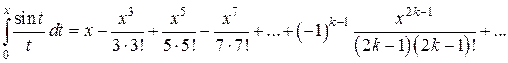 .
.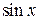 при любых значениях
при любых значениях  , с любой заданной степенью точности. Так,
, с любой заданной степенью точности. Так,  с точностью до 0,01:
с точностью до 0,01: 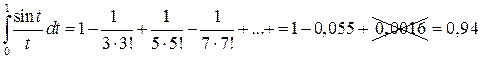
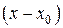 , тем самым выделяются главные части. После этого производятся необходимые сокращения, вследствие чего неопределенность обычно исчезает.
, тем самым выделяются главные части. После этого производятся необходимые сокращения, вследствие чего неопределенность обычно исчезает.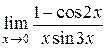 .
.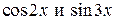 в степенные ряды из табл. 8.1, находим
в степенные ряды из табл. 8.1, находим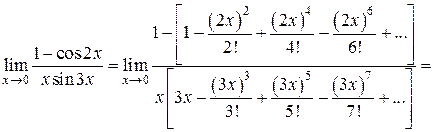
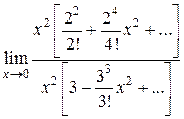 .
.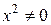 и выполнив переход к пределу почленно в числителе и знаменателе, окончательно получим
и выполнив переход к пределу почленно в числителе и знаменателе, окончательно получим 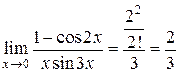 .
.


