Метод обхода ГрэхемаВыпуклые оболочки Задача вычисления (построения) выпуклой оболочки не только является центральной в целом ряде приложений, но и позволяет разрешить ряд вопросов вычислительной геометрии, на первый взгляд не связанных с ней. Построение выпуклой оболочки конечного множества точек, и особенно в случае точек на плоскости, уже довольно широко и глубоко исследовано и имеет приложения, например, в распознавании образов [Akl, Toussaint (1978); Duda, Hart (1973)], обработке изображений [Rosenfeld (1969)], а также в задаче раскроя и компоновки материала [Freeman (1974); Sklansky (1972); Freeman-Shapira (1975)]. Основные понятия и идеи Понятие выпуклой оболочки множества точек S является естественным и простым. В соответствии с определением — это наименьшее выпуклое множество, содержащее S. Чтобы наглядно представить это понятие в случае, когда S — конечное множество точек на плоскости, предположим, что это множество охвачено большой растянутой резиновой лентой. Когда лента освобождается, то она принимает форму выпуклой оболочки. Предметом этой лекции является построение выпуклой оболочки на плоскости. Эта задача, как правило, ставится следующим образом. Задано множество S, содержащее N точек, требуется построить их выпуклую оболочку. Вашему вниманию будут представлены некоторые методы, позволяющие решить эту задачу. Ещё одним понятием, которое нам понадобится, является понятие крайней точки. Точка выпуклого множества S называется крайней, если не существует пары точек a, b Î S таких, что p лежит на открытом отрезке ab. Множество E крайних точек S в точности совпадает с множеством вершин выпуклой оболочки S. Используя это свойство, мы приходим к основной идее алгоритма поиска: 1. Определить крайние точки. 2. Упорядочить эти точки так, чтобы они образовывали выпуклый многоугольник. Необходима теорема, которая позволит нам проверять, является ли некоторая точка крайней. Теорема 1. Точка р не является крайней плоского выпуклого множества S только тогда, когда она лежит в некотором треугольнике, вершинами которого являются точки из S, но сама она не является вершиной этого треугольника (рис. 12).
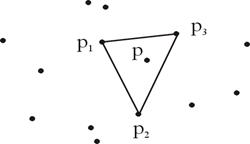
Рис. 1 Точка р не является крайней, так как она находится внутри треугольника (p1p2p3). Эта теорема дает идею для алгоритма удаления точек, не являющихся крайними. Имеется О(N 3) треугольников, определяемых N точками множества S. Проверка принадлежности точки заданному треугольнику может быть выполнена за некоторое постоянное число операций, так что за время О (N 3) можно определить, является ли конкретная точка крайней. Повторение этой процедуры для всех N точек множества S потребует времени O(N 4). Хотя наш алгоритм является чрезвычайно неэффективным, он очень прост в идейном плане и показывает, что крайние точки могут быть определены за конечное число шагов. Мы затратили время О(N4) только на определение крайних точек, которые должны быть как-то упорядочены, чтобы образовать выпуклую оболочку. Смысл этого порядка раскрывается следующими теоремами. Теорема 3.5. Луч, выходящий из внутренней точки ограниченной выпуклой фигуры F, пересекает границу F в точности в одной точке. Теорема 3.6. Последовательные вершины выпуклого многоугольника располагаются в порядке, соответствующем изменению угла относительно любой внутренней точки. Если даны крайние точки некоторого множества, то его выпуклую оболочку можно найти, выбрав точку q, про которую известно, что она является внутренней точкой оболочки, и упорядочив затем крайние точки в соответствии с полярным углом относительно q. Сортировку можно провести за O(N log N) шагов. Таким образом мы показали, что задача поиска выпуклой оболочки может быть решена за время O(N4). Метод обхода Грэхема Алгоритм со временем выполнения 0(N4) не позволит обрабатывать очень большие наборы данных. В этом разделе мы исследуем наш алгоритм с точки зрения наличия в нем ненужных вычислений. Так ли необходимо проверять все треугольники, определяемые множеством из N точек, чтобы узнать, лежит ли некоторая точка в каком-либо из них? Если пет, то имеется некоторая надежда, что крайние точки можно найти за время, меньшее чем О (N4). Грэхем в одной из первых работ, специально посвященных вопросу разработки эффективных геометрических алгоритмов [Graham (1972)], показал, что, выполнив предварительно сортировку точек, крайние точки можно найти за линейное время. Использованный им метод стал очень мощным средством в области вычислительной геометрии. Предположим, что внутренняя точка уже найдена, а координаты других точек тривиальным образом преобразованы так, что найденная внутренняя точка оказалась в начале координат (для этого можно использовать полярную систему координат). Упорядочим N точек в соответствии со значениями полярного угла и расстояния от начала координат. Сравнение расстояний необходимо выполнять лишь в случае, если две точки имеют один и тот же полярный угол, но тогда они лежат на одной прямой с началом координат, и сравнение в этом случае тривиально. Представив упорядоченные точки в виде дважды связанного кольцевого списка, получаем ситуацию, представленную на рис. 13. Обратите внимание: если точка не является вершиной выпуклой оболочки, то она является внутренней точкой для некоторого треугольника (O pq), где р и q— последовательные вершины выпуклой оболочки. Суть алгоритма Грэхема состоит в однократном просмотре упорядоченной последовательности точек, в процессе которого удаляются внутренние точки. Оставшиеся точки являются вершинами выпуклой оболочки, представленными в требуемом порядке.
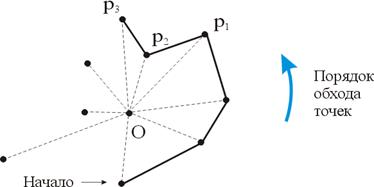
Рис. 2. Начало обхода точек в методе Грэхема. Вершина р2 удаляется, если угол p1p2p3 оказывается вогнутым. Просмотр начинается с точки, помеченной как НАЧАЛО, в качестве которой можно взять самую правую с наименьшей ординатой точку из данного множества, заведомо являющуюся вершиной выпуклой оболочки. Тройки последовательных точек многократно проверяются в порядке обхода против часовой стрелки с целью определить, образуют или нет они угол, больший или равный л. Если внутренний угол p1p2p3 больше или равен л, то говорят, что р1р2р3, образуют «правый поворот», иначе они образуют «левый поворот». Из выпуклости многугольника непосредственно следует, что при его обходе будут делаться только левые повороты. Если р1р2р3 образуют правый поворот, то р2 не может быть крайней точкой, так как она является внутренней для треугольника (Op1p3). В зависимости от результата проверки угла, образуемого текущей тройкой точек, возможны два варианта продолжения просмотра: 1. p1p2p3 образуют правый поворот. Удалить вершину р2, и проверить тройку p0p1p3. 2. p1p2p3 образуют левый поворот. Продолжить просмотр, перейдя к проверке тройки p2p3p4. Просмотр завершается, когда, обойдя все вершины, вновь приходим в вершину НАЧАЛО. Заметим, что вершина НАЧАЛО никогда не удаляется, так как она является крайней точкой и поэтому при отходе назад после удаления точек, мы не сможем уйти дальше точки, предшествующей точке НАЧАЛО. Простой анализ показывает, что такой просмотр выполняется лишь за линейное время. Рассмотренный метод обхода границы многоугольника называется методом обхода Грэхема. Ниже дано более точное описание этого алгоритма. procedure ОБОЛОЧКА-ГРЭХЕМА(S) 1. Найти внутреннюю точку q. 2. Используя q как начало координат, упорядочить точки множества S лексикографически в соответствии с полярным углом и расстоянием от q. Организовать точки множества в виде кольцевого дважды связанного списка со ссылками СЛЕД и ПРЕД и указателем НАЧАЛО на первую вершину. Значение true логической переменной f указывает на то, что вершина НАЧАЛО оказалась достигнутой при прямом продвижении по оболочке, а не в результате возврата. 3. (Обход) Begin v:= НАЧАЛО; w:= ПРЕД[ v ]; f:= false; while (СЛЕД[ v ] ¹ НАЧАЛО or f = false) do Begin if (СЛЕД[ v ]= w) then f:=true; if (три точки: v, СЛЕД[ v ], СЛЕД[СЛЕД[ v ]] образуют левый поворот) then v:= СЛЕД[ v ] else begin УДАЛИТЬ СЛЕД[ v ]; v:=ПРЕД[ v ] End End End. По окончании выполнения алгоритма список содержит упорядоченные нужным образом вершины оболочки. Итак, мы приходим к следующему выводу: выпуклая оболочка N точек на плоскости может быть найдена за время О(N log N) при памяти О(N) с использованием только арифметических операций и сравнений. Если вспомнить нижнюю оценку, обсуждавшуюся в разд. 1, то видно, что этот простой и изящный алгоритм имеет оптимальное время выполнения. Однако имеется одно обстоятельство, которое может вызвать некоторое беспокойство у читателя, — это использование полярных координат. В самом деле, это предполагает выполнение преобразования координат, что может быть затруднительным в системах с ограниченным набором примитивных операций. Кроме того, рассмотренный алгоритм является оптимальным в худшем случае, но мы, однако, не изучили его поведение в среднем. И ещё одно замечание заключается в том, что так как алгоритм основывается на теореме 3, применимой только в случае плоскости, алгоритм не имеет обобщения на случай пространств более высокой размерности. Поэтому имеет смысл рассмотреть какие-то другие методы решения проблемы, не обременённые вышеуказанными недостатками.
|