дисперсии которых неизвестны и одинаковы(малые независимые выборки)
Даны две генеральные совокупности Х и Y, имеющие нормальное распределение. Есть основание выдвинуть гипотезу о равенстве генеральных средних этих совокупностей, то есть Сделаем независимые выборки, объем которых nx и ny (nx, ny <30), по данным выборок вычислим выборочные средние Выборочные средние, как правило, различаются. Тогда возникает вопрос: значимо (существенно) или незначимо (несущественно) различаются выборочные средние? Различие между выборочными средними будет значимым, если нулевая гипотеза несправедлива, то есть генеральные средние неодинаковы, что и вызвало различие выборочных средних. А если нулевая гипотеза справедлива, то различие выборочных средних незначимо, оно объясняется случайными причинами. Для того чтобы выявить значимость различий выборочных средних, воспользуемся случайной величиной
Можно показать, что эта случайная величина имеет распределение Стьюдента с k = nx + ny - 2 степенями свободы. Однако нулевую гипотезу можно проверить по этому критерию только в том случае, если дисперсии данных генеральных совокупностей одинаковы. Поэтому если в условии задачи ничего не известно о генеральных дисперсиях, то предварительно проверяется вспомогательная гипотеза о равенстве генеральных дисперсий. Если получим, что дисперсии равны, то далее проверяется основная гипотеза по критерию Стьюдента, в противном случае решение задачи прекращается. Итак, если проверка показала, что генеральные дисперсии равны, то находим наблюдаемое значение критерия по данным выборок:
Затем нужно найти критическую точку. Для этого необходимо знать критическую область, которая строится в зависимости от вида конкурирующей гипотезы. Возможны несколько способов выбора гипотезы Н 1. 1. Н 0: М (Х) = М (Y); Н 1: М (Х) > М (Y). Такой вид гипотезы Н 1 возможен только если по данным выборок Правосторонняя критическая точка находится по таблице критических точек распределения Стьюдента (прил. 5) при уровне значимости a, помещенном в нижней строке таблицы, и по числу степеней свободы k = nx + ny - 2. Затем, сравнивая Т набл с t крит. пр(a, k), делают вывод. Если Т набл > t крит. пр(a, k), то есть наблюдаемое значение критерия попало в критическую область (рис. 2), то нулевая гипотеза отвергается, справедлива конкурирующая гипотеза Н 1: М (Х) > М (Y); расхождение между выборочными средними значимо (существенно). А если Т набл < t крит. пр(a, k), то есть наблюдаемое значение критерия попало в область принятия гипотезы, то нет оснований отвергать нулевую гипотезу, по данным наблюдения она принимается. Расхождение между выборочными средними несущественно (случайное). 2. Н 0: М (Х) = М (Y); Н 1: М (Х) < М (Y). Такой вид гипотезы Н 1 возможен только если по данным выборок Распределение Стьюдента симметрично относительно нуля, тогда t крит. л = - t крит. пр. В силу этого предварительно следует найти t крит. пр (a, k), как было описано в случае 1, а затем уже t крит. л(a, k))=- t крит. пр (a, k). Далее сравнивается Т набл с t крит. л(a, k). Если Т набл < t крит. л(a, k), то есть наблюдаемое значение критерия попало в критическую область (рис. 4), то нулевая гипотеза отвергается, справедлива конкурирующая гипотеза Н 1: М (Х) < М (Y). Расхождение между выборочными средними значимо. А если Т набл > t крит. л(a, k), то есть наблюдаемое значение критерия попало в область принятия гипотезы, то нет оснований отвергать нулевую гипотезу по данным наблюдения М (Х) = М (Y). Расхождение между выборочными средними случайное (за счет случайности выборки). 3. Н 0: М (Х) = М (Y); Н 1: М (Х) Эта конкурирующая гипотеза может быть выдвинута при любом соотношении между Так как распределение Стьюдента симметрично относительно нуля, то и критические точки симметричны относительно нуля, то есть t крит. л(a, k) = - t крит.пр (a, k). Поэтому критическая область становится симметричной, а критические точки t крит. л и t крит. пр при справедливости нулевой гипотезы находят из условия
Отсюда следует, что достаточно найти только t крит. дв(a, k) = t крит. пр(a, k). Критическая точка двусторонней критической области t крит.дв находится по таблице критических точек распределения Стьюдента при заданном уровне значимости a, помещенном в верхней строке таблицы, и по числу степеней свободы k = nx + ny - 2 (прил. 5 файла «Приложения»). Далее сравниваем Т набл с t крит. дв(a, k) и делаем вывод. Если А если Рассмотренный критерий имеет широкое практическое применение, например, при сравнении размеров двух партий деталей, изготовленных на двух одинаково настроенных станках, или при сравнении средней производительности труда рабочих двух бригад, работающих в одинаковых условиях, и т.д.
Рис. 2
Рис. 3 Рис. 4 Замечание. При проверке гипотезы о равенстве генеральных средних при заданном уровне значимости a контролируется лишь ошибка первого рода, но нельзя ничего сказать о степени риска, связанного с принятием неверной гипотезы, то есть с возможностью ошибки второго рода. Пример 3. По двум независимым выборкам, объемы которых nx = 12 и ny = 18, извлеченным из нормально распределенных генеральных совокупностей Х и Y, найдены выборочные средние Решение. Даны совокупности Х и Y, имеющие нормальный закон распределения. Требуется проверить гипотезу Н 0: М (Х) = М (Y). Так как о генеральных дисперсиях ничего не известно, то с помощью случайной величины Н 0: D (Х) = D (Y) при Н 1: D (Х) > D (Y). Находим F набл = Так как F набл < F крит (0,01; 11; 17), то есть F набл попало в область принятия гипотезы, нет оснований отвергать нулевую гипотезу по данным наблюдения D (Х) = D (Y); расхождение между исправленными выборочными дисперсиями случайное. Следовательно, можно проверить основную гипотезу. Предварительно выбираем конкурирующую гипотезу. В данном случае их может быть две: 1) Н 1: М (Х) № М (Y); 2) Н 1: М (Х) > М (Y), так как Проверяем гипотезу Н 0 в первом случае: Н 0: М (Х) = М (Y), Н 1: М (Х) № М (Y). Воспользуемся случайной величиной
которая имеет распределение Стьюдента с k=nx + ny -2 = 12+18-2 = 28 степенями свободы. По данным выборок найдем Т набл По таблице критических точек распределения Стьюдента находим t крит.дв(0,01; 28) = 2,76 (при двусторонней критической области). Сравниваем Т набл и t крит.дв(0,01; 28). Так как Ѕ Т наблЅ> tкрит.дв (0,01; 28), то есть Т набл попало в критическую область (рис. 3), нулевая гипотеза отвергается, справедлива конкурирующая: Н 1: М (Х) № М (Y), а следовательно, расхождение между выборочными средними значимо. Проверим гипотезу Н 0 во втором случае: Н 0: М (Х) = М (Y), Н 1: М (Х) > М (Y). Т набл» 7,09; t крит.пр(0,01, 28) = 2,46 (при правосторонней критической области). Т набл > t крит.пр(0,01; 28) (рис. 2), вывод такой же, как и в первом случае. Пример 4. Из двух партий изделий, изготовленных на двух одинаково настроенных станках, извлечены малые выборки, объемы которых 10 и 12. Получены следующие результаты:
При уровне значимости 0,05 проверить гипотезу о равенстве средних размеров изделий, предполагая, что результаты измерений имеют нормальный закон распределения. Решение. Признак Х - размер изделий, изготовленных на первом станке. Признак Y - размер изделий, изготовленных на втором станке. Признаки имеют нормальный закон распределения. Требуется проверить гипотезу Н 0: М (Х) = М (Y). Для проверки нулевой гипотезы сделаны выборки объемами nx = 10 и ny = 12. По выборочным данным найдем точечные оценки параметров данных распределений. Расчеты приведем в таблице:
Так как о генеральных дисперсиях ничего не известно, предварительно проверим вспомогательную нулевую гипотезу Н 0: D (Х) = D (Y) при конкурирующей Н 1: D (Х) > D (Y). По выборочным данным проверяем гипотезу с помощью случайной величины Находим F набл = Так как F набл < F крит (a, k 1, k 2), то есть наблюдаемое значение критерия попало в область принятия гипотезы, нет оснований отвергать нулевую гипотезу по данным наблюдения D (Х) = D (Y), расхождение между исправленными дисперсиями случайное. Следовательно, можно проверить основную гипотезу. Для ее проверки выбираем конкурирующую гипотезу. В данном случае можно взять Н 1: М (Х) № М (Y), либо Н 1 :М (Х) > М (Y). Односторонняя критическая область дает более точный результат проверки гипотезы, поэтому берем вторую конкурирующую гипотезу. Итак, Н 0: М (Х) = М (Y), Н 1: М (Х) > М (Y). Проверяем нулевую гипотезу с помощью случайной величины
которая имеет распределение Стьюдента с k = nx + ny -2 = 10 + 12 - Т набл По таблице критических точек распределения Стьюдента находим t крит.пр(0,05, 20) = 1,73. Так как Т набл > t крит.пр (0,05; 20), то есть наблюдаемое значение критерия попало в критическую область (рис. 2), то нулевая гипотеза отвергается, а принимается конкурирующая гипотеза Н 1: М (Х) > М (Y); расхождение между выборочными средними значимо, а следовательно, средние размеры изделий, изготовленных на двух одинаково настроенных станках, различные.
|

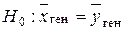 или Н 0: М (Х) = М (Y). При заданном уровне значимости a требуется проверить нулевую гипотезу.
или Н 0: М (Х) = М (Y). При заданном уровне значимости a требуется проверить нулевую гипотезу. , а также выборочные исправленные дисперсии
, а также выборочные исправленные дисперсии 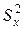 и
и  .
.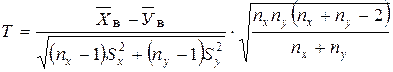 .
. .
. . В этом случае конкурирующая гипотеза определяет правостороннюю критическую область
. В этом случае конкурирующая гипотеза определяет правостороннюю критическую область  , которая строится при справедливости нулевой гипотезы, исходя из требования
, которая строится при справедливости нулевой гипотезы, исходя из требования  (Т>tкрит .пр (a, k))=a.
(Т>tкрит .пр (a, k))=a. . Конкурирующая гипотеза определяет левостороннюю критическую область
. Конкурирующая гипотеза определяет левостороннюю критическую область 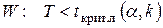 . Критическая точка t крит. л(a, k) вычисляется, исходя из требования
. Критическая точка t крит. л(a, k) вычисляется, исходя из требования 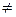 М (Y).
М (Y).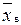 и
и  . Она определяет двустороннюю критическую область
. Она определяет двустороннюю критическую область 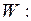 Т<tкрит . л(a, k) или Т>tкрит . пр (a, k), которая строится, исходя из требования
Т<tкрит . л(a, k) или Т>tкрит . пр (a, k), которая строится, исходя из требования  .
.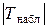 > t крит. дв(a, k), то есть наблюдаемое значение критерия попало в критическую область (рис. 3), то нулевая гипотеза отвергается, справедлива конкурирующая гипотеза Н 1: М (Х)
> t крит. дв(a, k), то есть наблюдаемое значение критерия попало в критическую область (рис. 3), то нулевая гипотеза отвергается, справедлива конкурирующая гипотеза Н 1: М (Х) 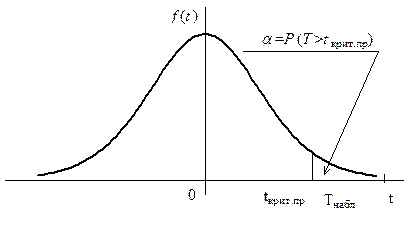
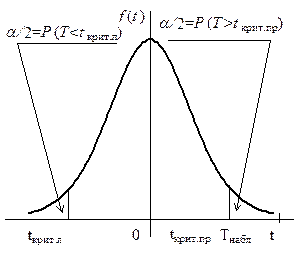
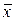 в = 31,2 и
в = 31,2 и  в = 29,2 и исправленные дисперсии
в = 29,2 и исправленные дисперсии 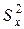 = 0,84 и
= 0,84 и  = 0,40. При уровне значимости 0,01 проверить гипотезу о равенстве генеральных средних.
= 0,40. При уровне значимости 0,01 проверить гипотезу о равенстве генеральных средних. , которая имеет распределение Фишера - Снедекора с k 1 = nх - 1 = 11 и k 2 = ny - 1 = 17 степенями свободы (n 1 = nх, так как
, которая имеет распределение Фишера - Снедекора с k 1 = nх - 1 = 11 и k 2 = ny - 1 = 17 степенями свободы (n 1 = nх, так как 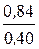 = 2,1. F крит (a, k 1, k 2) = F крит (0,01;11;17) = 3,52. Сравниваем F набл и F крит(0,01; 11; 17).
= 2,1. F крит (a, k 1, k 2) = F крит (0,01;11;17) = 3,52. Сравниваем F набл и F крит(0,01; 11; 17).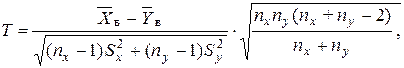
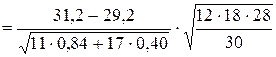 » 7,09.
» 7,09.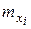
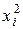
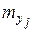
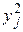
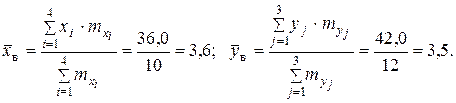
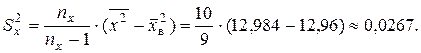

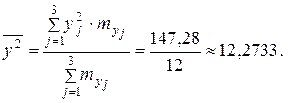

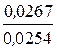 » 1,05. По таблице критических точек распределения Фишера - Снедекора имеем F крит(0,05; 9, 11) = 2,90.
» 1,05. По таблице критических точек распределения Фишера - Снедекора имеем F крит(0,05; 9, 11) = 2,90.
 » 14,49.
» 14,49.


