Основні властивості порівняньВластивість1. Відношення порівнянності чисел за модулем є відношенням еквівалентності. Властивість 2. Порівняння за одним модулем можна почленно додавати, віднімати, множити, тобто якщо а º b (mod m), c º d (mod m), то а ± с ≡ b ± d (mod m), аc º bd (mod m). Наслідки: Члени порівняння можна переносити із однієї частини в другу з протилежним знаком. До однієї частини порівняння можна додавати або віднімати від неї любе число, кратне модулю. Обидві частини порівняння можна підносити до ступеню з натуральним показником. Властивість 3. Обидві частини порівняння можна поділити на їхній спільний дільник, якщо він взаємно простий з модулем. Властивість 4. Обидві частини порівняння і модуль можна ділити на любий їх спільний дільник. Властивість 5. Якщо а º b (mod m), то (а, m) = (b, m). Приклад 1. Довести, що при будь-якому n Î N (5 × 72(n +1) + 23 n ) Запишемо цю умову у вигляді порівняння: 5 × 72(n +1) + 23 n º 0(mod 41) Скористаємося властивостями порівнянь. 5 × 72 n × 72 + 8 n º 0(mod 41) 5 × 49 n × 49 + 8 n º 0(mod 41) 5 × 8 n × 8 + 8 n º 0(mod 41) 8 n × (40 + 1) º 0(mod 41) 41 × 8 n º 0(mod 41) 0 × 8 n º 0(mod 4 0 º 0(mod 41) – тотожне порівняння, що доводить вірність твердження.
Відношення порівнянності цілих чисел за модулем m є бінарним відношенням еквівалентності на множині цілих чисел, бо має властивості: 1) рефлективності: а º а (mod m); 2) симетричності: якщо а º b (mod m), то b º а (mod m); 3) транзитивності: якщо а º b (mod m) та b º с (mod m), то а º с (mod m). Тому множина цілих чисел розбивається на класи еквівалентності. В один і той же клас попадають числа, які дають одні і ті ж остачі при діленні на m, звідки випливає, що класів еквівалентності рівно m. Класи еквівалентності називають класами лишків за даним модулем. Лишком (або представником цього класу) за модулем m називають будь-яке число цього класу. Таким чином, до класу лишків, який містить число а, належать усі цілі числа х виду х = а + mt, де t Î Z. Цей клас позначають символом
Теорема 1. Множина класів лишків відносно операцій додавання та множення класів утворює комутативне кільце з одиницею Z m. Теорема 2. В кільці Z m немає дільників нуля, якщо m – просте число. Теорема 3. Z m є полем, якщо m – просте число. Теорема 4. Множина класів лишків взаємно-простих з модулем m утворює абелеву мультиплікативну групу.
За модулем m виділяють повну та зведену системи лишків. Означення. Повною системою лишків (ПСЛ) за модулем m називають будь-яку систему лишків, утворену з m чисел, взятих по одному з кожного класу лишків. Існують дві основні повні системи лишків: 1) повна система найменших невід’ємних лишків за модулем m – система остач від ділення на m. Ця система містить лишки 0, 1, 2, 3,…, m –1; 2) повна система абсолютно найменших лишків за модулем m. Якщо лишки цієї системи позначити через ai, i= Означення. Якщо (a, m) = 1, то клас Означення. Зведеною системою лишків (ЗСЛ) за модулем m називають будь-яку систему лишків, утворену з j(m) чисел, взятих по одному з кожного класу, взаємно простого з модулем m. Нагадаємо, що j (m) – значення функції Ейлера від числа m. Обчислити значення функції Ейлера можна за формулами: 1) j (р) = р – 1, якщо р – просте число; 2) j (рk) = pk- 1 (p – 1 ), k Î N, р – просте число; 3) j (a × b) = j (a) × j (b), якщо (a, b) = 1. Приклад 1. Виписати ПСЛ та ЗСЛ за модулем m =12. 1) Повна система найменших невід’ємних лишків: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11. 2) Повна система абсолютно найменших лишків: За умовою 0, ±1, ±2, ±3, ±4, ±5, 6 або 0, ±1, ±2, ±3, ±4, ±5, –6. 3) Зведена система лишків. Підрахуємо кількість елементів у цій системі. Знайдемо j(12) = j(22) × j(3) = 4. У системі 4 елементи. В повній системі найменших невід’ємних лишків знайдемо лишки, взаємно прості з числом 12: (0, 12)¹1, (1, 12)=1, (2, 12)¹1, (3, 12)¹1, (4, 12)¹1, (5, 12)=1, (6, 12)¹1, (7, 12)=1, (8, 12)¹1, (9, 12)¹1, (10, 12)¹1, (11, 12)=1. Зведена система лишків: 1, 5, 7, 11. Велике значення в теорії чисел відіграють теореми Ейлера і Ферма. Теорема Ейлера. Якщо a ÎZ, m ÎN, m > 1 i (a, m) = 1, то аj(m) º 1(mod m). Наступна теорема є наслідком теореми Ейлера. Теорема Ферма. Якщо р – просте, (а, р) = 1, то ар º а (mod р). Дійсно, оскільки р – просте, то j (р) = р – 1. Тоді за теоремою Ейлера матимемо ар- 1º 1(mod р). Помножимо обидві частини порівняння на а: ар º а (mod р), що потрібно було довести. Приклад 2. Чи виконується теорема Ейлера для чисел:1) а = 2, m = 15; 2) a = 3, m = 18? 1) Оскільки (2, 15) = 1, то теорему Ейлера можна застосувати. Маємо: 2 j (15) º 1(mod 15). j (15) = j (3 × 5) = j (3) × j (5) = 2 × 4 = 8 28 º (24)2 º 162 º 1(mod 15). 2) Оскільки (3, 18) = 3, то теорему Ейлера застосувати не можна. Дійсно, j(18) = j(32) × j(2) = 3 × 2 = 6. 36 = 34 × 32 = 81 × 9 º 9 × 9 = 81 º 9(mod 18) Порівнянням ступеня n з одним невідомим за модулем m називають порівняння виду: f(x)=anxn+an-1xn-1+…+a1x+a0 º0 (mod m), (1) де ліва частина – многочлен ступеня n з цілими коефіцієнтами, an Якщо a – число, яке задовольняє (1), то розв’язок порівняння записують у виді x º a (mod m). Порівняння з одним невідомим називають рівносильними, якщо множини їхніх розв’язків збігаються. Операції, які не порушують множину розв’язків порівняння (їх називають елементарними перетвореннями): а) додавання до обох частин порівняння будь-якого многочлена з цілими коефіцієнтами; б) додавання до однієї частини порівняння многочлена з коефіцієнтами, кратними модулю; в) множення (ділення) обох частин порівняння на число, яке взаємно просте з модулем. Ми будемо розглядати порівняння 1-го ступеню з однім невідомим, тобто порівняння виду: ax º b (mod m). Теорема про кількість розв’язків. Якщо у порівнянні ax º b (mod m): 1) (a, m) = 1, то порівняння має єдиний розв’язок; 2) (a, m) = d, d > 1 i b 3) (a, m) = d, d > 1 i b Приклад 3. Визначити кількість розв’язків порівняння: а) 84 х º –60 (mod 36); б) –175 х º 105 (mod 50); в) 119 х º 44 (mod 52). а) a = 84, m = 36, b = –60. Знаходимо, що (a, m)=(84, 36)=12, і 60 б) a = – 175, m = 50, b = 105. Знаходимо, що (a, m)=(175, 45)=25, і 105 в) a= 119, m =52, b =44. Знаходимо, що (a, m)=(119, 52)=1, тому порівняння має єдиний розв’язок. Зауваження. Перед розв’язанням порівняння, необхідно визначити кількість його розв’язків. Після розв’язання порівняння необхідно зробити перевірку. При розв’язанні порівняння доцільно замінити коефіцієнти порівняння найменшими невід’ємними або найменшими за абсолютною величиною лишками за даним модулем.
Лекція 10 1. Обґрунтувати методи розв’язку порівнянь першого ступеня. Навести приклади рішень. 2. Дати поняття невизначеного рівняння. Розглянути випадок невизначеного рівняння першого ступеня з двома невідомими та метод його рішення за допомогою теорії порівнянь. 3. Дати поняття системи порівнянь, рішення системи порівнянь. Довести китайську теорему. Найбільш поширеними способами розв’язування порівнянь виду (2) є наступні: 1. Спосіб спроб. Якщо порівняння має розв’язки, то їх можна знайти, якщо замість невідомої підставляти числа повної системи лишків за модулем m. Цей спосіб використовується при невеликих значеннях модуля. Приклад 1. Розв’язати порівняння 63 x º 7 (mod 5). (63,5)=1, порівняння має єдиний розв’язок. Замінимо порівняння рівносильним (це можна було б зробити і на першому кроці), зменшувши відповідні коефіцієнти: 63 x º 7(mod 5) 3 x º 2(mod 5). Випробуємо лишки з повної системи абсолютно найменших лишків за модулем 5, тобто числа 0; ±1; ±2. Маємо: х =0: 3 × 0 = 0 х =1: 3× 1 = 3 х = – 1: 3 × (– 1) = – 3 º 2 (mod 5). Випробування можна припинити, оскільки порівняння має єдиний розв'язок: x º – 1 º 4(mod 5). Перевірка: (63× 4 – 7) 2. Штучний спосіб. Зведення даного порівняння за допомогою елементарних перетворень до рівносильного йому порівняння з коефіцієнтом при невідомому, який дорівнює 1. Приклад 2. Розв’язати порівняння 15 х = 8 (mod 13). 15 х = 8 (mod 13). (15, 13)=1, порівняння має єдиний розв’язок. 15 х – 13 х = 8 (mod 13) 2 х = 8 (mod 13) х º 4 (mod 13) Перевірка: (15 × 4 – 8) = 52 Одним з найбільших загальних способів одержування ознак подільності є ознака Паскаля. Теорема. Для того щоб число а = аnаn- 1 … а 1 а 0ділилось на натуральне число m, необхідно і достатньо, щоб на m ділилась сума f (а) = an ∙ rn + an- 1∙ rn- 1 +…+ а 1 ×r 1 + a 0 ×r 0, де rі Виведемо ознаку подільності на 3, на 9. Нехай а = аn ×10 n + аn- 1×10 n- 1+…+ а 1×10 + а0. Так як 10 k f(а) = аn + аn- 1+…+ а 1+ а 0. За ознакою Паскаля, число а Виведемо ознаку подільності на 11. Нехай а = аn ×10 n + аn- 1×10 n- 1+…+ а 1×10 + а 0. 10 k ≡ 1(mod 11), якщо k – парне, і 10 k ≡ – 1(mod 11), якщо k – непарне. Тому f(а) = а 0 – а 1 + а 2 – а 3+...= (а 0+ а 2+…) – (а 1 + а 3 +…). За ознакою Паскаля, число а
|

 41.
41. Представником класу лишків
Представником класу лишків 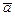 може бути будь-який елемент цього класу:
може бути будь-який елемент цього класу: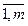 ,то їх можна знайти за умовою
,то їх можна знайти за умовою 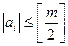 .
.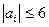 ,
,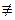 1(mod 18).
1(mod 18).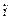 m. Означення. Розв’язком порівняння (1) називають клас лишків за модулем m, кожне число якого задовольняє це порівняння.
m. Означення. Розв’язком порівняння (1) називають клас лишків за модулем m, кожне число якого задовольняє це порівняння. d, то порівняння має d розв’язків;
d, то порівняння має d розв’язків;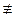 2 (mod 5)
2 (mod 5) 10 і (mod m), і =
10 і (mod m), і =  .
.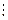 3(9) (число ділиться на 3(9) тоді і тільки тоді, коли на 3 (9) ділиться сума цифр цього числа).
3(9) (число ділиться на 3(9) тоді і тільки тоді, коли на 3 (9) ділиться сума цифр цього числа).


