Нестационарная задача теплопроводности для полуограниченного телаПрименим метод преобразования Лапласа для решения задачи теплопроводности для полуограниченного тела (бесконечно длинного стержня, боковая поверхность которого имеет идеальную теплоизоляцию). Температура полуограниченного тела во всех точках имеет определенное значение, заданное некоторой функцией ¦(х), превышающей значение температуры окружающей среды. В начальный момент времени конец стержня принимает температуру Тс, которая поддерживается постоянной в течение всего процесса теплообмена. Найти распределение температуры по длине стержня в любой момент времени. Математически задача формулируется следующим образом. Имеем дифференциальное уравнение
при краевых условиях
Вначале для упрощения задачи положим Тс=0 (в случае неравенства нулю температуры среды, можно осуществить замену переменной Т). Применим преобразование Лапласа к дифференциальному уравнению.
Таким образом, дифференциальное уравнение в частных производных для оригинала функции Т(x,t) превращается в обыкновенное дифференциальное уравнение для изображения ТL(x,s), так как ТL(x,s) не зависит от времени t. При этом переходе используется начальное условие. Перепишем уравнение (3.2) в виде
Рассмотрим более простую задачу, когда температура стержня до охлаждения всюду одинакова и равна Т0, т.е.
Общее решение дифференциального уравнения (3.4) для изображения можно записать в следующем виде:
где А1 и В1 – постоянные, определяемые из граничных условий. Применим преобразование Лапласа к граничным условиям:
Воспользуемся вторым граничным условием:
из которого следует, что А1=0. В противном случае первый член правой части этого уравнения неограниченно возрастает с ростом х. Воспользуемся первым граничным условием:
Тогда решение для изображения будет иметь вид:
Для нахождения оригинала применим обратное преобразование Лапласа:
В нашей задаче
откуда получаем:
Функция erf(U) изменяется от 0, когда U=0 до 1, когда U стремится к бесконечности (практически когда U > 2,7, так как erf(2,7)=0,9999).
Если температура конца стержня не равна нулю, а равна
Следовательно, постоянная
Применив обратное преобразование Лапласа, получим решение для оригинала:
где
Решение также можно представить в виде:
|

 (t>0, 0 < х < ¥) (3.1)
(t>0, 0 < х < ¥) (3.1)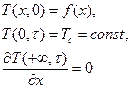

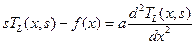 (3.2)
(3.2)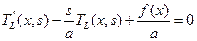 (3.3)
(3.3) . В этом случае уравнение (3.3) примет более простой вид:
. В этом случае уравнение (3.3) примет более простой вид: (3.4)
(3.4)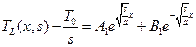 , (3.5)
, (3.5)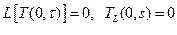 ,
,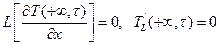 .
. ,
, .
. (3.6)
(3.6) .
. . Следовательно, решение задачи будет иметь вид:
. Следовательно, решение задачи будет иметь вид: , (3.7)
, (3.7)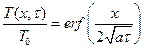 . (3.8)
. (3.8)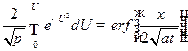 называется функцией ошибок Гаусса.
называется функцией ошибок Гаусса. , то граничное условие перепишется в виде:
, то граничное условие перепишется в виде: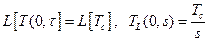 .
.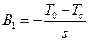 , так как Т0 > Тс. Тогда решение для изображения примет вид:
, так как Т0 > Тс. Тогда решение для изображения примет вид: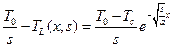 . (3.9)
. (3.9)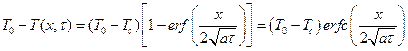 , (3.10)
, (3.10)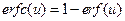 .
. . (3.11)
. (3.11)


