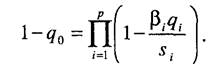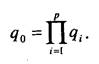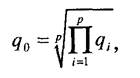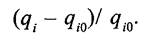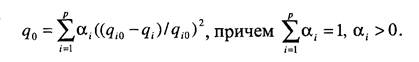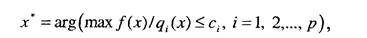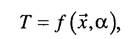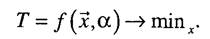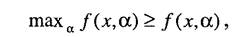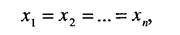Выбор как максимизация критерия 1 страница

Если теперь сделать еще одно важное предположение, что выбор любой альтернативы приводит к однозначно известным последствиям (т.е. считать, что выбор осуществляется в условиях определенности) и заданный критерий q(x) численно выражает оценку этих последствий, то наилучшей альтернативой х * является, естественно, та, которая обладает наибольшим значением критерия:

х*= arg max q(x), при условии, что х е X.

Задача определения оптимального решения х*, простая по постановке, часто оказывается сложной для решения, поскольку метод ее решения (да и сама возможность решения) определяется как характером множества X, так и видом критерия. На возможность решения задачи оптимизации критерия оказывает влияние размерность вектора х и тип множества X - является ли оно конечным, счетным или континуальным. В свою очередь критерий может быть сформулирован в виде функции или функционала.

Однако сложность определения наилучшей альтернативы на практике существенно возрастает, так как оценивание любого варианта единственным числом обычно оказывается неприемлемым упрощением. Более полное рассмотрение альтернатив приводит к необходимости оценивать их не по одному, а по нескольким критериям, качественно различающимся между собой. При решении конкретных задач системным аналитикам следует учитывать множество критериев: технических, технологических, экономических, социальных, эргономических и пр.

Итак, пусть для оценивания альтернатив используется несколько критериев qi(х), i = \,..., p. Теоретически можно представить себе случай, когда в множестве X окажется одна альтернатива, обладающая наибольшими значениями всех p критериев; она и является наилучшей. Однако на практике такие случаи почти не встречаются, и возникает вопрос, как же тогда осуществлять выбор.

Путь к единому параметру оптимизации часто лежит через обобщение. Из многих критериальных функций, определяющих альтернативу, трудно выбрать один, самый важный. Будем рассматривать ситуацию, когда необходимо множество критериальных функций свернуть в единый количественный признак. Каждый критерий в общем случае имеет свой физический смысл и свою размерность. Чтобы объединить различные критерии, прежде всего, приходится вводить для каждого из них некоторую безразмерную шкалу. Шкала должна быть однотипной для всех объединяемых критериев - это делает их сравнимыми.

Сведение многокритериальной задачи к однокритериальной

Рассмотрим наиболее употребительные способы решения многокритериальных задач. Первый способ состоит в том, чтобы многокритериальную задачу свести к однокритериальной. Это означает введение суперкритерия, т.е. скалярной функции векторного аргумента:

Ч₀(^х) ⁼ % (?,(*). Я₂{х),..., q_p(x)).

Суперкритерий позволяет упорядочить альтернативы по величине q_o, выделив тем самым наилучшую (в смысле этого критерия). Вид функции q_o определяется тем, как мы представляем себе вклад каждого критерия в суперкритерий. Обычно для реализации данной процедуры используют аддитивные

или мультипликативные функции

Коэффициенты s. обеспечивают безразмерность критериального значения (частные критерии могут иметь разную размерность, и тогда некоторые арифметические операции над ними, например сложение, не имеют смысла). Коэффициенты а., (3. отражают относительный вклад частных критериев в суперкритерий.

Итак, при данном способе задача сводится к максимизации суперкритерия:

Очевидные достоинства объединения нескольких критериев в один суперкритерий сопровождаются рядом трудностей и недостатков, которые необходимо учитывать при использовании этого метода.

Рассмотрим примеры построения обобщенных критериальных показателей. Пусть рассматриваемая альтернатива характеризуется п частными критериальными функциями q_t(i-\, 2,..,p). Каждая из функций q. имеет свой физический смысл и, чаще всего, свою размерность. Введем простейшее преобразование: набор данных для каждого q. поставим в соответствие с самым простым стандартным аналогом -шкалой, на которой имеется только два значения: 0 - брак, неудовлетворительное качество, 1 - годный продукт, удовлетворительное качество. В ситуации, когда каждый преобразованный критерий принимает только два значения 0 и 1, естественно желать, чтобы и обобщенный критерий принимал одно из двух возможных значений, причем так, чтобы значение 1 имело место тогда и только тогда, когда все частные критериальные показатели приняли бы значение равное 1. Если же, хотя бы один из показателей принял значение, равное 0, то и обобщенный критерий будет равным нулю. В этом случае для построения обобщенного критериального показателя естественно воспользоваться формулой

Иногда применяют запись

где q - обобщенный критериальный показатель; q. - частные критериальные функции.

Если для каждого из частных критериев известен «идеал», к которому нужно стремиться, то можно предложить следующий метод построения обобщенного параметра оптимизации (критериального показателя). Пусть q._o - наилучшее (идеальное) значение z-го критерия. Тогда (<7, - Ч_т) ~ ^меР^ близости к идеалу. Поскольку при построении обобщенного критериального показателя необходимо, чтобы различные показатели были сопоставимы, надо привести их к безразмерному значению. Это можно осуществить, отнормировав полученное отклонение следующим образом

Чтобы исключить влияние знаков, возведем последнее выражение в квадрат

Тогда обобщенный критериальный показатель можно записать

Если все частные критерии совпадают с идеалом, то q₀ станет равным нулю. В таком правиле определения обобщенного критериального показателя каждый частный критерий входит в формулу на равных правах. На практике показатели бывают далеко не равноправны. Введем некоторые весовые коэффициенты ос., тогда правило определения обобщенного параметра можно записать в виде:

Задача определения значений весовых коэффициентов - это отдельная задача, она не входит в рамки обсуждения.

Если удается построить обобщенный критериальный показатель, то метод поиска оптимального решения будет аналогичен методу оптимизации в случае единственного критерия. В зависимости от вида критериального показателя в качестве метода решения могут быть использованы прямые оптимизационные процедуры, в случае невозможности аналитического решения используются численные методы.

Условная максимизация

Вторым способом решения задач выбора в условиях наличия нескольких критериальных показателей является сведение задачи к задаче условной максимизации. Данный метод решения задач выбора целесообразно применять в тех случаях, когда заведомо известно, что частные критерии неравнозначны между собой, одни из них более важны, чем другие. В этом случае происходит выделение основного, главного критерия, остальные рассматриваются как вспомогательные, дополнительные к выделенному. Такое разделение критериев позволяет сформулировать задачу принятия решений как задачу определения условного экстремума:

где через/(х) обозначен основной критерий; q.(x) - вспомогательные или второстепенные критериальные функции. В ограничениях могут иметь место различные сочетания знаков: от строгого равенства до строгого неравенства. Например, если вспомогательный критерий характеризует стоимость затрат, то разумнее задавать их верхний уровень и формулировать задачу с ограничениями в виде неравенств. Для решения задач в такой постановке разработаны специальные методы математического программирования, рассмотренные в гл. 2 работы [57].

Нахождение паретовского множества

Следующий способ многокритериального выбора состоит в сравнении альтернатив между собой по всем сформированным критериям и выделении подмножества наилучших альтернатив. В данном подходе отказываются от поиска одной единственной наилучшей альтернативы. Решающее правило в этом случае строится на основе аксиомы В. Парето, которая формулируется следующим образом: «Если в задаче принятия решений частные критерии независимы по предпочтению и значение каждого из них желательно увеличивать, то из двух альтернатив, характеризуемых набором частных критериев, предпочтительнее та, для которой выполняются соотношения q_u(x) > q_2i(x) по всем i, где первый индекс характеризует номер стратегии, второй индекс -номер частного критерия. То есть первая альтернатива предпочтительнее второй только в том случае, когда значения ее частных критериев не меньше значений частных критериев второй альтернативы. Если все значения частных критериев одной альтернативы равны значениям критериев другой, то альтернативы равнозначны». Таким образом, предпочтение одной альтернативе перед другой можно отдавать только если первая по всем критериям лучше второй. Если же предпочтение хотя бы по одному критерию расходится с предпочтением по другому, то такие альтернативы признаются несравнимыми. В результате попарного сравнения альтернатив все худшие по всем критериям альтернативы отбрасываются, а все оставшиеся несравнимые между собой принимаются. Если все максимально достижимые значения частных критериев не относятся к одной и той же альтернативе, то принятые альтернативы образуют множество Парето и выбор на этом заканчивается. При необходимости выбора единственной альтернативы следует привлекать дополнительные соображения: либо корректировать систему предпочтений, либо обращаться к услугам экспертов, либо воспользоваться методами, рассмотренными ранее (построение обобщенного критерия или сведение задачи к задаче поиска условного экстремума).

13.3. Выбор в условиях неопределенности

Рассмотренные до настоящего времени задачи осуществления выбора формулировались таким образом, что последствия сделанного выбора предполагались однозначно определенными. Выбор одной из альтернатив был связан с известным однозначным следствием. В этом случае проблема выбора состояла в сравнении разных вариантов, т.е. альтернатив.

В реальной практике в большинстве случаев приходится иметь дело с более сложной ситуацией, когда выбор альтернативы неоднозначно определяет последствия сделанного выбора. Адекватное реальности описание проблемы практически всегда содержит различного рода неопределенности, отражающие то естественное положение, в котором находится исследователь: любое его знание относительно и неточно. Принято различать три типа неопределенностей. С одной стороны это неопределенности природы. К данному виду неопределенностей относят факторы, неизвестные исследователю. Далее неопределенности противника. Нередки ситуации, когда исследователь принимает решения в условиях, при которых результаты его решений не строго однозначны. Они зависят от действий других лиц (партнеров, противников и т.п.), которые он не может учесть или предсказать. И, наконец, существуют так называемые неопределенности целей. Такая ситуация возникает в случае, когда при принятии решений формулируется несколько целей, которые в общем случае могут противоречить друг другу. В этом случае мы приходим к многокритериальной задаче выбора. Подходы к принятию решения в условиях многокритериальной задачи рассмотрены в предыдущем параграфе.

Существует также классификация неопределенностей по соотношению альтернатив и исходов. Различают неопределенности дискретного и непрерывного типа, стохастические и расплывчатые неопределенности.

Рассмотрим следующую ситуацию: имеется набор возможных исходов у е Y, из которых один окажется совмещенным с выбранной альтернативой, но какой именно - в момент выбора неизвестно, а станет ясным позже, когда выбор уже сделан и изменить ничего нельзя. Будем предполагать, что с каждой альтернативой х связано одно и то же множество исходов Y, для разных альтернатив одинаковые исходы имеют разное значение. В случае дискретного набора альтернатив и исходов такую ситуацию можно изобразить с помощью матрицы, представленной в табл. 13.1:

Таблица 13.1

	У\		У)		У-
Х\	<?"		Чч		Ч\т
Xi	*i		Чч		Qim
х„			Чч		Чгт

В этой матрице все возможные исходы образуют вектору = (у,,..., у_т), числа q.. выражают оценку ситуации, когда сделан выбор альтернативы х.п реализовался исходу.. В конкретных случаях числа q.. могут иметь различный смысл: это может быть «выигрыш», «потери», «платежи» и т.п. Если все строки q. = (q_n,..., q_jm) при любых г одинаковы, то проблемы выбора нет. Если же строки матрицы различны, возникает вопрос, какую альтернативу предпочесть, не зная заранее, какой из исходов реализуется.

Аналогичная ситуация возникает в случае, когда множества X и Y непрерывны. В этом случае зависимость между альтернативами и исходами задается в виде функции q(x,y),x e X,y e Yc соответствующей постановкой вопроса о выборе х.

Введенных до настоящего времени параметров недостаточно для формальной постановки задачи выбора. При различной конкретизации этой задачи она приобретает различный смысл и требует различных методов решения. Методологической базой для решения такого рода задач является теория игр. Метод решения конкретной задачи будет зависеть от характера воздействующих на ситуацию факторов, не зависящих от лица, принимающего решения. Здесь необходимо различать уже отмеченные ранее неопределенности природы и неопределенности противника. В задачах выбора с природной неопределенностью считается, что исходы у = (у_р..., у_т) есть возможные состояния природы. Желательность каждой альтернативы х, зависит от того, каково состояние природы, но узнать это состояние исследователь сможет лишь после того, как сделан выбор.

В задачах выбора с неопределенностью противника предполагается, что исходы Y- это множество альтернатив, на котором выбор осуществляет второй игрок. В отличие от природной неопределенности игрок преследует свои интересы, отличные от интересов исследователя (первого игрока). При этом матрица Q = Ц^Ц, характеризующая оценки ситуаций с точки зрения системного исследователя или лица, принимающего решения, выбирающего х, уже недостаточна для описания всей ситуации. Необходимо задать вторую матрицу и = ||м_;,.|, описывающую систему предпочтений с позиции противника. Задание X, Y, <2 и [/называется нормальной формой игры. Расхождение между матрицами Q и U определяет степень антагонизма лица, принимающего решения, и его противника. Остановимся на анализе природных неопределенностей и неопределенностей противника.

Природные неопределенности

Рассмотрение природных неопределенностей начнем с примера. Пусть перед системным аналитиком стоит задача проложить маршрут океанского лайнера и распорядиться запасом горючего так, чтобы судно как можно быстрее дошло до пункта назначения. При этом известно, что время нахождения в пути будет существенно зависеть от погодных условий на трассе в момент ее прохождения. В данном случае погодные условия представляют собой природную неопределенность. Ситуация типична для ряда задач принятия решений. Рассмотрим ее формализацию. Запишем целевую функцию, например время нахождения судна в пути, в следующем виде

где а е G_a - некоторый параметр, который заранее неизвестен. Выбор альтернативы х, которая бы минимизировала значение целевой функции будет существенно зависеть от того, какое значение параметра а реализуется в момент прохождения судна по трассе. Таким образом, говоря о природной неопределенности, имеем в виду, что выбор осуществляется в условиях, когда целевая функция задана, но не совсем точно, а именно, она содержит неопределенный параметр. Постановка задачи выбора будет выглядеть следующим образом

При этом решение будет представлять собой функцию от параметра а: х =х(ос). Если никакой дополнительной информацией о факторе неопределенности ос лицо, принимающее решение, не располагает, то результат оптимизации произволен. В реальных ситуациях информация о параметре ос обычно имеет вид ос е G, где G - некоторое множество. Но подобной информации также недостаточно для однозначного решения задачи. Решение х = х(ос) определяет лишь некоторое отображение множества неопределенности природных факторов G_a на множество альтернатив X, которое естественно назвать множеством неопределенности результата. Множество неопределенности результатах- важная характеристика процедуры принятия решений, но его построение сопряжено с большим объемом сложных вычислений.

Рассмотрим другой подход, который дает строгую оценку. Данный подход основан на применении принципа наилучшего гарантированного результата. Суть его состоит в следующем. Так как для любой альтернативы х справедливо неравенство

Число f *, определенное данным способом, называется гарантированной оценкой, а соответствующая альтернатива х - х* - гарантированной стратегией в том смысле, что каково бы ни было значение параметра неопределенности ос, выбор х = х* гарантирует, что при любом а значение целевой функции будет не меньше, чем f*.

Выбор гарантирующей стратегии поведения - это рациональный способ принятия решений. В результате использования данной стратегии лицо, принимающее решение, гарантирует исход, защищенный от всевозможных случайностей. Каковы бы ни были неконтролируемые факторы, в результате такого выбора обеспечивается значение целевой функции не меньше, чем/*. Данный результат может быть улучшен, если принять решение, связанное с определенным риском. Критерии принятия решений в условиях риска рассмотрим несколько позже.

Неопределенности противника

Перейдем теперь к описанию неопределенностей, связанных с существованием активных партнеров или противников, действия которых лицо, принимающее решение, не может полностью контролировать.

В теории принятия решений особое место занимает изучение ситуации, в которой участвует много субъектов (много оперирующих сторон), причем каждый из них стремится достичь своей цели

и имеет для этого определенные возможности, которые описываются вектором х, х е X. Заметим, что формально такая ситуация включает в себя проблему многокритериальности, требующую определения вектора х, при котором достигается максимум критериев ffX). В самом деле, если отождествить цель каждого из субъектов с его критерием ДХ), а в качестве описания множествах принять условия

то в результате будет получен частный случай задачи со многими активными партнерами. Общий случай ситуации со многими субъектами гораздо сложнее и требует для своего анализа целый ряд специфических гипотез. Поясним это на примере двух субъектов. Итак, пусть два субъекта Aw. Б, располагающие возможностью выбора векторов х и у, стремятся к достижению своих целей, которые будем записывать в виде

В частном случае может оказаться, что/(х, у) - - ф(х, у); такую ситуацию называют антагонистической. Антагонистические ситуации были предметом множества исследований и сделались основным объектом изучения в теории игр. Чисто антагонистическая ситуация является в известном смысле вырожденной. Наиболее типичен конфликт, в котором интересы партнеров или противников не совпадают, но и не строго противоположны.

Общий случай нетождественности интересов (целей) партнеров (субъектов) называют конфликтом. При изучении конфликтных ситуаций, т.е. при изучении возможных способов выбора, удобно отождествлять исследователя с одним из субъектов. Условимся называть лицо, принимающее решение субъектом А.

В связи с тем, что исход выбора зависит от выбора субъекта Б, необходимо принять ту или иную гипотезу о его поведении, которое, в свою очередь, будет зависеть от характера информированности субъекта Б. Здесь возможно существование нескольких гипотез (нескольких • случаев).

1) Каждый из субъектов не имеет никакой информации о выборе, который сделал другой субъект. В этом случае имеется возможность найти гарантированную оценку. Для субъекта А она будет выражаться формулой

f=max_xmin_yf(x,y), для субъекта Б - формулой

ф* = max min _x ф(х, у).

Решая сформулированные задачи, определяют векторы х* и у*, которые реализуют значения/* и ф*. Такое решение означает, что сделав выбор х = х*, лицо, принимающее решение, при любых условиях (любом выборе у е У) гарантирует, что значение целевой функции/(х, у) будет не меньше, чем/*.

В этой ситуации могут быть предложены различные варианты риска. Например, имеется возможность принять гипотезу о том, что другой субъект использует гарантирующую стратегию у = у*. Тогда необходимо делать другой выбор:

/* =ma.x_xf(x,y').

В этом случае определяется вектор х = х¹ и соответствующее значение функции/=/'. При этом/¹ > /, но если противник сделает иной выбор, например, у - у\ то может оказаться, что/(х', у¹) </*. В данной ситуации следует иметь в виду, что риск есть риск, и если исследователь сформулировал гипотезу и она оказалась неверной, то и результат может оказаться не тем, который ожидается.

2) Вторая ситуация характеризуется тем, что исследователь во время принятия решения имеет информацию о выборе субъекта Б, т.е. ему известно выбранное субъектом Б значение у.

Тогда стратегию (выбор) х следует искать в виде функции х = х(у). Данная стратегия может быть определена эффективно, для этого требуется решить задачу оптимизации

f⁽²⁾ =тзх _xf(x,y).

Решая данную оптимизационную задачу, определяем искомую стратегию х = х(у). Для этого случая можно также вычислить гарантированный результат (он будет отличен от/*):

/ =minmax_xf(x,y)

и во всех случаях / > / *.

Заметим, что выбирая свою стратегию - вектор х - лицо, принимающее решение, никак не можем повлиять на выбор, который сделал другой субъект.

3) Предположим теперь, что субъект Б в момент принятия своего решения будет знать выбор лица, принимающего решение (субъектаЛ); например, субъект Л обязан сообщить свое решение субъекту Б. В этом случае исключается возможность оказать влияние на выбор, который сделает субъект Б. В самом деле, если исследователь знает целевую функцию субъекта Б, то естественно сделать предположение о том, что субъект Б будет делать выбор из условия

ф = тах_уф(.х,;у).

Решая данную задачу исследователь может определить отклик субъекта Б на свой выбор, который, согласно сформулированной гипотезе, будет оптимальной стратегией субъекта Б:

У = У(х)-

Теперь имеется возможность распорядиться выбором вектора х. Подставляя последнее выражение в формулу для целевой функцииДх, у), можно получить

f(x,y(x)) = F(x).

Свой выбор исследователь может сделать из условия

/<³> = F(x).

Итак, информация о том, что субъект Б будет знать выбор лица, принимающего решения, а также гипотеза о том, что субъект Б выберет свою оптимальную стратегию, позволяют так воздействовать на его выбор, чтобы он в максимальной степени соответствовал целям исследователя.

Описанная ситуация достаточно часто встречается на практике и ей нетрудно придать ту или иную экономическую интерпретацию. Так, вектор х можно отождествить с ресурсом, а функцию у = у(х) назвать производственной функцией, которая описывает наивыгоднейший для субъекта Б способ использования ресурса. Таким образом, субъекту Б выделяется такое количество ресурса, чтобы его деятельность наилучшим образом соответствовала целям субъекта А.

Критерии сравнения альтернатив

Теория принятия решений в настоящее время представляет собой самостоятельную научную дисциплину. По данному направлению опубликовано множество монографий [3], поэтому не имеет смысла подробно останавливаться на результатах данной теории. Изложим основополагающие идеи и подходы к решению задач теории принятия решений.

Центральным моментом данной теории является введение критерия для оценки выбираемого варианта. В силу неопределенности исхода требуется дать оценку сразу целой строке матрицы (см. табл. 13.1). Имея такие оценки для всех строк, и сравнивая их, можно приступать к решению задачи выбора. Для этого требуется ввести критерии сравнения альтернатив.

Самым распространенным является уже рассмотренный ранее максиминный критерий, который гарантирует результат выбора по принципу «наименьшего из зол». Рассмотрим суть данного критерия применительно к табл. 13.1 (матрица платежей). В каждой из строк матрицы определяем наименьший из выигрышей minjqij, который характеризует гарантированный выигрыш в самом худшем случае. Данное значение считаем оценкой альтернативы х.. Далее определяем альтернативу х'', обеспечивающую наибольшее значение этой оценки:

х* = are max. min. a...

Эта альтернатива называется оптимальной по максиминному критерию. Если платежную матрицу определить не через выигрыш, а через проигрыш, то тот же принцип рассмотрения приводит к минимаксному критерию. Минимаксный критерий использует оценочную функцию, соответствующую позиции крайней осторожности. Правило выбора решения в соответствии с минимаксным критерием можно интерпретировать следующим образом: матрица платежей, на основании которой осуществляется поиск оптимального решения, дополняется еще одним столбцом из наименьших результатов q._r каждой строки. Выбрать надлежит те варианты х., в строках которых стоят наибольшие значения q._r этого столбца.

Выбранные таким образом варианты полностью исключают риск. Это означает, что лицо, принимающее решение, не может столкнуться с худшим результатом, чем тот, на который он ориентируется. Какие бы условия ни сложились при развитии ситуации, соответствующий результат не может оказаться ниже q. Это свойство заставляет считать минимаксный критерий одним из фундаментальных. В задачах системных исследований применительно к техническим системам данный критерий находит наиболее широкое применение. Однако следует заметить, что положение об отсутствии риска стоит различных потерь. Осознавая данную ситуацию, в теории принятия решений предложено большое количество критериев, учитывающих всевозможные особенности конкретных задач и предпочтений субъектов, принимающих решения. Это такие критерии как Байеса-Лапласа, Сэвиджа, Гурвица, Ходжа-Лемана, Гермейера и т.д. Детальное описание данных критериев можно найти, например, в [3].

Применение минимаксного критерия бывает оправдано в ситуациях, которые характеризуются следующими обстоятельствами:

• о возможности появления внешних состояний ничего не известно;

• приходится считаться с возможностью появления нескольких различных по своему характеру негативных внешних состояний;

• решение реализуется лишь один раз;