Преломление лучей сферической поверхностью
Получим формулу для определения положения точки А2, являющейся изображением точки А1. При этом будем рассматривать только лучи, составляющие с оптической осью столь малые углы, что практически можно считать, что При этом учтем правила знаков. Пусть луч А1М падает на сферическую поверхность под углом i. Сопряженный ему луч МА2 (угол преломления r) пересечет оптическую ось в некоторой точке А2. Обозначим А1О = -а1; А2О = +а2; ОС = R (радиус сферы). Из треугольников МА1С и СМА2 по теореме синусов имеем:
или
После несложных преобразований приведем последнее выражение к виду:
Из (1.9) видно, что преломлении на сферической поверхности произведение
выражение называется уравнением параксиального (нулевого луча). При малых углах и все лучи, исходящие из точечного объекта А1, после преломления пересекаются в точке А2. Для параксиальных лучей гомоцентрический пучок после преломления на сферической поверхности остается гомоцентрическим пучком и точка А2 является стигматическим изображением точки А1. Ограничиваясь рассмотрением параксиальных лучей, определим точку, через которую пройдут после преломления на сферической поверхности все лучи, которые можно выделить в параллельном пучке. Для этого в формуле (1.10) нужно предположить а1 =
Если а2
Точки, в которых пересекаются после преломления лучи, падающие на сферическую поверхность параллельным пучком, называются передним (F1) и задним (F2) фокусами. Сравнивая формулы (1.11) и (1.12), можно найти соотношения между фокусными расстояниями:
Из формулы (1.13) ясно, что фокусные расстояния пропорциональны показателям преломления сред, в которых лежат фокусы. Знак минус в правой части выражения (1.13) указывает на то, что переднее и заднее фокусное расстояния имеют разные знаки, то есть они лежат по разные стороны преломляющей поверхности. Преобразуя совместно уравнение параксиального (нулевого) луча (1.10) и уравнения (1.11), (1.12), можно получить формулу
Если отсчитать отрезки, определяющие положение точек А1 и А2 от переднего и заднего фокуса соответственно и обозначить эти отрезки через х1 и х2, то получим:
Подставляя эти выражения в (1.14), получим формулу Ньютона:
Применяя полученные результаты для сферического зеркала (п2=-п1), получим формулу сферического зеркала:
Фокусное расстояние сферического зеркала F = R/2. Фокус вогнутого зеркала действительный, фокус выпуклого зеркала мнимый. Для плоского зеркала
1.5. Увеличение. Уравнение Лагранжа – Гельмгольца
Стигматическое изображение точечного объекта получается тогда, когда оно формируется параксиальными лучами. Объясним теперь формирование изображений предметов, представляющих собой отрезок прямой, перпендикулярной к оптической оси (рис. 1.12).
Повернем оптическую ось А1С вокруг центра кривизны С на малый угол φ. При этом точка А1 займет положение В1’, а ее изображение – положение В2’. Все точки дуги А1В1’ отобразятся точками, находящимися на дуге А2В2’. Если указанные дуги малы, их можно заменить отрезками касательных А1В1 и А2В2, перпендикулярных к оптической оси А1С. Каждая точка изображения является местом пересечения всех лучей, исходящих из сопряженной точки объекта. Для нахождения этого места достаточно найти точку пересечения двух любых лучей. Удобно использовать лучи, направление распространения которых после преломления на сферической поверхности известно (рис. 1.13):
1) лучом В1М, параллельным оптической оси; после преломления он пройдет через задний фокус F2; 2) лучом В1F1N, проходящим через передний фокус F1; после преломления он пойдет параллельно оптической оси. Точка пересечения В2 этих двух лучей представляет собой изображение точки В1, а отрезок А2В2 является изображением отрезка А1В1. Отношение линейных размеров изображения к линейным размерам предмета называется линейным, или поперечным увеличением:
Напомним, что, в соответствии с правилом знаков, длины отрезков считаются положительными, если отрезки лежат над осью (изображение прямое), и отрицательными, – если отрезки лежат под осью (изображение перевернутое). Так как для небольших по размерам предмета и изображения выполняются соотношения:
то легко показать (см. рис. 1.13), что
Используя рис. 1.13 и формулу Ньютона, можно показать, что
Кроме линейного, система может характеризоваться угловым увеличением W, которое определяется как отношение тангенсов углов u2 и u1 (см. рис. 1.13):
Легко показать (см. формулы(1.18) и (1.20)), что При малом смещении предмета вдоль оси на величину dx1 изображение сместится вдоль оси на величину dx2. Продольным увеличением системы называется величина
Несложно показать, что U=V/W. Поперечное увеличение имеет значение для характеристики систем, проецирующих изображение на экран или фотопластинку (проекционные или фотографические объективы). Угловое увеличение важно при наблюдении удаленных объектов, когда стремятся увеличить угловые размеры рассматриваемых объектов (телескопические системы). Продольное увеличение характеризует резкость изображения пространственного объекта на экране. Рассматривая параксиальные лучи (см. рис. 1.13), нетрудно показать, что
или
Равенство (1.22) называют уравнением Лагранжа – Гельмгольца для параксиальной области. Из него следует, что преобразованием данного светового пучка оптической системой в другой пучок любого заданного строения невозможно. Это ограничение имеет особое значение в фотометрии и при решении задачи о концентрации световой энергии с использованием оптических систем. Инвариант Лагранжа-Гельмгольца является полным инвариантом, он применим для оптической системы, состоящей из произвольного числа преломляющих поверхностей, расположенных в любой среде. Этим он отличается от частного инварианта Аббе.
|

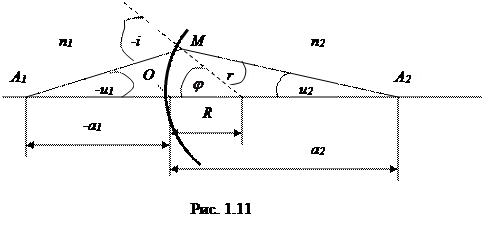 Пусть две однородные прозрачные среды с показателями преломления п1 и п2 разделены сферической поверхностью, радиус кривизны которой R. Проведем оптическую ось через точки А1, А2 и центр кривизны сферической поверхности С (рис. 1.11).
Пусть две однородные прозрачные среды с показателями преломления п1 и п2 разделены сферической поверхностью, радиус кривизны которой R. Проведем оптическую ось через точки А1, А2 и центр кривизны сферической поверхности С (рис. 1.11).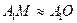 и
и 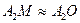 . Такие лучи называют параксиальными.
. Такие лучи называют параксиальными.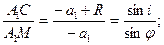
 ,
, .
.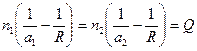 . (1.9)
. (1.9) не изменяет своей величины Q. Выражение (1.9) называют параксиальным (нулевым) инвариантом Аббе (немецкий физик-оптик). Представленное в виде
не изменяет своей величины Q. Выражение (1.9) называют параксиальным (нулевым) инвариантом Аббе (немецкий физик-оптик). Представленное в виде , (1.10)
, (1.10)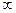 . С учетом этого условия получим заднее фокусное расстояние:
. С учетом этого условия получим заднее фокусное расстояние: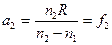 . (1.11)
. (1.11) , найдем переднее фокусное расстояние:
, найдем переднее фокусное расстояние: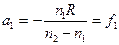 . (1.12)
. (1.12)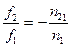 . (1.13)
. (1.13) . (1.14)
. (1.14) ,
,  .
. . (1.15)
. (1.15)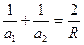 . (1.16)
. (1.16)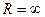 , и
, и  , то есть изображение точки в плоском зеркале мнимое и расположенное симметрично объекту относительно поверхности зеркала.
, то есть изображение точки в плоском зеркале мнимое и расположенное симметрично объекту относительно поверхности зеркала.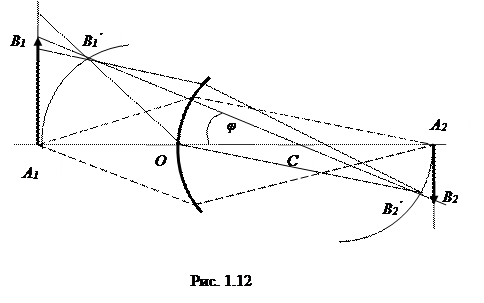

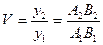 . (1.17)
. (1.17) ,
, или
или 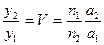 . (1.18)
. (1.18)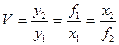 . (1.19)
. (1.19) . (1.20)
. (1.20)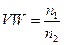 .
.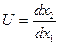 . (1.21)
. (1.21)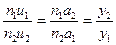 ,
,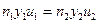 . (1.22)
. (1.22)


