МАКСИМАЛЬНЫЙ ПОТОК В ТРАНСПОРТНОЙ СЕТИ
Поток f в транспортной сети N – это функция, которая ставит в соответствие каждой дуге
В (3) и далее значком Транспортная сеть представляет собой модель доставки вещества (энергии, информации) от источника до стока по путям, которые связывают их через промежуточные пункты. При этом пропускная способность Кроме условий (2), (3) полагаем также, что
Из условия (3) следует, что
Здесь val (f) – мощность потока на сети. Как видно из (5), мощность потока является линейной функцией потоков по дугам. Сформулируем задачу о максимальном потоке на сети: найти совокупность Пусть множество вершин данной сети разбито на два непересекающихся подмножества A и B. Назовем разрезом
Известна теорема Форда-Фалкерсона: на любой сети максимальная мощность потока от источника s к стоку t равна минимальной пропускной способности разреза, отделяющего s от t. Этот теоретический результат лежит в основе следующего алгоритма построения максимального потока. 1. Построить какой-либо начальный набор 2. Сформировать подмножество A вершин, достижимых из источника s по ненасыщенным дугам. Если 3. Построить полупуть P из s в t, состоящий из ненасыщенных дуг; для построения кратчайшего пути использовать алгоритм поиска в ширину [3]. Определить
где
Сформировать новый поток
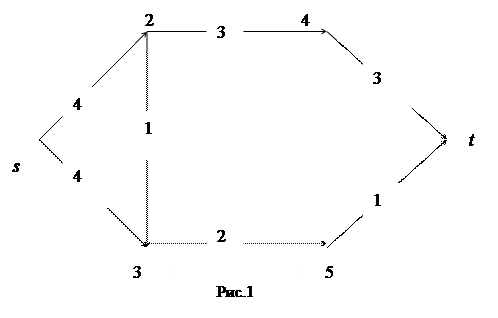
Положить k = k +1 и перейти к пункту 2 алгоритма. 4. Закончить выполнение алгоритма. Заметим, что в качестве начального можно использовать поток F 0, в котором f 0(i, j)=0 для всех дуг. При реализации данного алгоритма удобно использовать квадратные матрицы C =[ c (i, j)] для пропускных способностей и F =[ f (i, j)] для потоков. Рассмотрим пример решения задачи о максимальном потоке. Пример 1. На рис.1 приведена диаграмма транспортной сети. Пропускные способности дуг проставлены в разрывах линий.
Требуется построить на данной транспортной сети поток максимальной мощности. Составим матрицу пропускных способностей
Построим начальный поток F 0, который представлен на рис.2. В разрывах линий проставлены потоки по дугам.
Данный поток можно также задать матрицей
Мощность потока F 0 вычислим, просуммировав элементы данной матрицы в столбце, который соответствует стоку t. Получим val (F 0)=2+1=3. Далее, чтобы сформировать подмножество A, рассмотрим матрицу
Ненулевые элементы этой матрицы соответствуют ненасыщенным дугам. Рассмотрим в матрице C - F 0 строку, которая соответствует источнику s. Ненулевой элемент в строке соответствует дугам (s;2), (s;3). На основании этого составим для источника список: s ½½2, 3, и перейдем к строке, которая соответствует вершине 2. Находим ненулевые элементы этой строки. При этом не учитываем вершины, ранее появлявшиеся в списках. В результате для вершины 2 получаем: 2½½4. Продолжаем формирование таких списков до тех пор, пока не будет достигнут сток или не исчерпается возможность достижения вершин по ненасыщенным дугам (дальнейшее движение из вершины становится невозможным, если для нее получен пустой список). Для данного примера получим в результате: s ½½2, 3; 2½½4; 3½½5; 4½½ t. (9) Появление стока t в одном из списков говорит о том, что поток F 0 не является максимальным и его мощность можно увеличить. Восстановим полупуть из ненасыщенных дуг, по которому можно из источника s достичь стока t. Восстанавливается полупуть при просмотре списков вершин от конца (стока) к началу (источнику). В данном примере на основании списков (9) для вершин подмножества A получаем полупуть P: s -2-4- t. В соответствии с правилом (7) определяем Увеличим мощность потока в сети на величину D. Для этого пропускаем вдоль P дополнительно D единиц вещества. Пользуясь (8), строим поток F 1. Этот поток описывается матрицей
Далее строим матрицу
и повторяем для потока F 1 те действия, которые были проделаны для начального потока. При определении множества A получим: s ½½2, 3; 2½½Æ; 3½½5; 5½½Æ. (10) На основании (10) формируем подмножества A ={ s;2;3;5} и B ={4; t }. (11) Так как
Вычислим мощность максимального потока F 1. Для этого суммируем в матрице этого потока элементы, расположенные в последнем столбце (данный столбец соответствует стоку t). Получим val (F 1) = 3+1 = 4. Рассмотрев подмножества (11), определяем разрез минимальной пропускной способности, отделяющий источник от стока:
На основании (6) вычислим Пропускная способность разреза
|

 неотрицательное вещественное число
неотрицательное вещественное число  так, что удовлетворяются следующие условия:
так, что удовлетворяются следующие условия: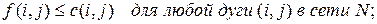 (2)
(2)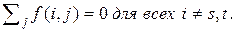 (3)
(3)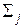 обозначено суммирование по всем номерам j вершин сети N. Дугу, для которой условие (2) выполняется в виде строгого равенства, будем далее называть насыщенной, а дугу, для которой условие выполняется со строгим неравенством, – ненасыщенной.
обозначено суммирование по всем номерам j вершин сети N. Дугу, для которой условие (2) выполняется в виде строгого равенства, будем далее называть насыщенной, а дугу, для которой условие выполняется со строгим неравенством, – ненасыщенной.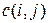 показывает, какое максимальное количество вещества может пройти по дуге за единицу времени; значение
показывает, какое максимальное количество вещества может пройти по дуге за единицу времени; значение  потока по дуге показывает, какое количество вещества в действительности проходит от вершины i к вершине j за единицу времени. Условие (2) называют ограничением по пропускной способности, условие (3) – условием сохранения. Условие сохранения означает, что в промежуточных вершинах сети N вещество не накапливается и не производится.
потока по дуге показывает, какое количество вещества в действительности проходит от вершины i к вершине j за единицу времени. Условие (2) называют ограничением по пропускной способности, условие (3) – условием сохранения. Условие сохранения означает, что в промежуточных вершинах сети N вещество не накапливается и не производится.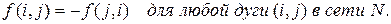 (4)
(4) (5)
(5) потоков всем по дугам сети, которая удовлетворяет условиям (2), (3), (4) и доставляет максимум функции (5). Данная задача может рассматриваться как задача линейного программирования, решение которой можно получить симплекс-методом. Возможно также построение максимального потока с помощью специальных приемов, которые требуют менее громоздких вычислений. Далее будет рассмотрен подход, использующий понятие разреза на сети.
потоков всем по дугам сети, которая удовлетворяет условиям (2), (3), (4) и доставляет максимум функции (5). Данная задача может рассматриваться как задача линейного программирования, решение которой можно получить симплекс-методом. Возможно также построение максимального потока с помощью специальных приемов, которые требуют менее громоздких вычислений. Далее будет рассмотрен подход, использующий понятие разреза на сети. на сети совокупность {(i, j)} дуг, у которых
на сети совокупность {(i, j)} дуг, у которых  и
и  . Если
. Если  и,
и, 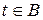 то говорят, что разрез
то говорят, что разрез  разреза и поток
разреза и поток  через разрез следующими выражениями:
через разрез следующими выражениями: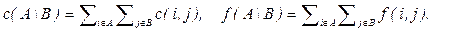 (6)
(6)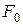 потоков по дугам, удовлетворяющий условиям (2), (3), (4). Положить k =0.
потоков по дугам, удовлетворяющий условиям (2), (3), (4). Положить k =0. , то поток максимальной мощности уже построен и задача решена – перейти к п.4 алгоритма; иначе перейти к п.3 алгоритма.
, то поток максимальной мощности уже построен и задача решена – перейти к п.4 алгоритма; иначе перейти к п.3 алгоритма.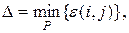 (7)
(7)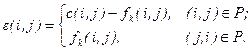
 , определив
, определив (8)
(8)


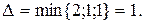
 , то F 1 является потоком максимальной мощности в данной транспортной сети. Данный поток представлен диаграммой на рис 3.
, то F 1 является потоком максимальной мощности в данной транспортной сети. Данный поток представлен диаграммой на рис 3.





