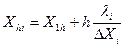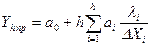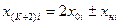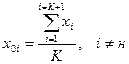Методы оптимизации

Одной из основных задач при исследовании различных процессов является возможность управления этим исследованием для обеспечения оптимальных условий его проведения. Наилучшим образом построить процесс, определить оптимальные режимы его проведения – естественное стремление исследователя. Однако до последнего времени эти вопросы решались интуитивно, на основе опыта разработчика и заказчика. Объясняется это необычайной сложностью современных процессов, обилием и разнообразием всевозможных внутренних связей в них. Ведь для выбора оптимального процесса необходимо сравнить его различные варианты, учесть и проанализировать влияние огромного числа факторов на параметры продукта этого процесса, – и все это нужно делать в ограниченные сроки разработки. Но оптимизация процесса в результате оказывается неэффективна.

Естественно, такое положение не может удовлетворять производство. Развитие вычислительной техники и кибернетики вызвало значительные изменения в методике оптимизации технологических процессов.

Из предыдущих разделов видно, что природа процесса и задачи, стоящие перед исследователем, определяют тип модели, наиболее приемлемой для исследуемого процесса. Сложность технологических процессов производства обуславливает особенности подхода к анализу и управлению ими, а так же делает нецелесообразным полную и глубокую расшифровку механизма явлений, происходящих в них. В том случае, когда неизвестна теория процессов и необходимо принимать решения в условиях неопределенности, желательно научиться управлять процессом эмпирически. В соответствии с этим для описания технологических процессов наиболее приемлемыми являются имитационные модели в виде полинома n -ого порядка, а при исследовании процессов экспериментально – статистические методы.

Одним из первых этапов при оптимизации технологических процессов является определение критерия оптимизации – функции отклика Y, значение которой будет положено в основу оценки процесса при его оптимизации.

Параметр оптимизации должен соответствовать следующим требованиям:

· параметр должен измеряться при любом изменении (комбинации) режимов технологического процесса;

· параметр должен быть статистически эффективным, то есть измеряться с наибольшей точностью;

· параметр должен быть информативным, то есть всесторонне характеризовать технологический процесс (операцию);

· параметр должен иметь физический смысл, то есть должна быть возможность достижения полезных результатов при соответствующих условиях процесса;

· параметр должен быть однозначным, то есть должно минимизироваться или максимизироваться только одно свойство изделия.

Задача оптимизации сводится к нахождению таких условий проведения технологического процесса, при которых критерий оптимизации достигает экстремума.

При исследовании технологических процессов аналитическая зависимость Y (X) (где X – вектор управляемых, а следовательно, контролируемых факторов) неизвестна и исследователь не может найти экстремум путем решения системы дифференциальных уравнений

дy (X)/ дx_i=0

при i =1,2.. k; где k – число факторов.

Обычно исследователь может лишь наблюдать значения выходной величины при различных комбинациях входных факторов (x ₁, x ₂,.. x_k); в действительности наблюдается сумма истинного значения и случайной ошибки опыта:

y _набл = y _ист + Δ

Принято называть геометрическое изображение функции отклика в факторном пространстве (x ₁, x ₂,.. x_k) – поверхностью отклика.

При поиске экстремальной точки, в отличии от аналитического исследования, осуществляется локальное изучение поверхности отклика по результатам ряда опытов, специально поставленных около исходной точки. Движение к экстремуму в n-мерном пространстве независимых переменных осуществляется обычно не непрерывно, а шагами. Анализируя результаты экспериментов и сравнивая их, исследователь принимает решение о дальнейших действиях по поиску оптимума. Экстремальное значение отклика достигается с помощью многократного последовательного изучения поверхности отклика и продвижения в факторном пространстве. Существует несколько экспериментальных методов оптимизации, различающихся способом определения направления движения и организацией самого движения.

Метод Гаусса-Зайделя. При оптимизации по этому методу последовательное движение к экстремуму осуществляется путем поочередного варьирования каждым фактором до достижения очередного экстремума функции отклика.

 

 

 

 

 

На рисунке изображены кривые равного выхода для одного из технологических процессов. Таким образом, изображающая точка перемещается попеременно вдоль каждой из координатных осей X_i факторного пространства, переход к новой (i +1)-й координате осуществляется при достижении частного экстремума целевой функции Y (X) по предыдущей координате, то есть в точке X _ih, где

Здесь и далее будем предполагать, что ищем экстремум функции в виде минимума функции отклика, максимум находится аналогично, меняется только знак.

После достижения частного экстремума при изменении значений последнего фактора X_k, переходят снова к варьированию первым фактором и так далее; в результате изображающая точка приближается к экстремуму. Направление движения вдоль (i +1)-ой координатной оси выбирается обычно по результатам двух пробных опытов в окрестностях точки частного экстремума по предыдущему фактору. Поиск экстремума прекращается в точке, движение из которой в любом направлении не приводит к уменьшению значения выходного параметра. Точка поверхности отклика, в которой значение функции отклика будет минимальным, и будет искомым оптимумом. Точность определения оптимальной точки зависит от шага варьирования Δ X_i, и иногда для увеличения точности уменьшают величину шага при приближении к экстремуму.

Важным моментом при постановке эксперимента является выбор исходной точки и интервала варьирования. Здесь необходимо учитывать всю имеющуюся априорную информацию о исследуемом процессе.

Основным недостатком метода являются большие временные затраты при движении к экстремуму. При увеличении количества переменных до 5-6 применение данного метода становится неэффективным.

Метод случайного поиска. Характерной чертой этого метода является случайный выбор направления движения на каждом шаге, то есть одновременное изменение значений сразу всех факторов. Так, если изображающая точка после i -ого шага занимает X _i положение в факторном пространстве, то следующий рабочий шаг будет сделан лишь после выполнения пробного эксперимента в точке X _{i 1} =X _i +Z, где Z – случайный вектор определенной длинны рис. 4

Значения функции Y (X _i) и Y (X _i + Z) сравниваются и производится (i +1)-й рабочий шаг вдоль вектора по направлению к экстремуму. Как правило, длина рабочего шага превышает длину пробного.

Критерием выхода в область экстремума является возрастание числа неудачных шагов, то есть многократное повторение положения, когда Y (X _i)< Y (X _i + Z).

Очевидно, что метод случайного поиска очень прост, однако он применим только для очень простых ситуаций. Основным недостатком метода являются большая трудоемкость и длительность поиска экстремума, а также возможность ошибки при попадании в область локального экстремума.

Метод градиента. При оптимизации градиентным методом движение осуществляется в направлении наибольшего изменения критерия оптимизации, то есть в направлении градиента целевой функции. Причем, как и в методе случайного поиска, направление движения корректируется после каждого рабочего шага, то есть каждый раз заново определяется значение градиента по результатам специально поставленных пробных экспериментов (рис. 5).

Поскольку координатами вектора

служат коэффициенты при линейных членах разложения функции Y (X) в ряд Тейлора по степеням x_i, то соответствующие компоненты вектора градиента могут быть получены, как коэффициенты a₁, a₁, …a_i, …a_n линейной аппроксимации поверхности отклика вблизи исходной точки x₀.

Линейные коэффициенты обычно оцениваются экспериментально. Наиболее просто каждый из коэффициентов a_i определяется по результатам двух пробных экспериментов в окрестности исходной точки. В этом случае приращение целевой функции Δ y_i, соответствующее приращению Δ x_i, можно считать пропорциональным значению частной производной дy/дx_i ≈ a_i.

После нахождения составляющих градиента выполняется рабочий шаг по направлению к экстремуму

где

p – параметр рабочего шага.

Показателем выхода в область экстремума является малое значение модуля градиента, то есть все коэффициенты a_i становятся незначимыми или равными нулю.

Объем эксперимента в каждой точке равен 2 n, где n – число факторов, оказывающих влияние на выходной параметр. Одним из важных вопросов при оптимизации любым методом является выбор величины рабочего шага. Если шаг очень мал, то потребуется большое количество шагов, и, следовательно, опытов, то есть движение к оптимуму будет очень медленным; если размеры шага слишком велики, то есть возможность проскочить экстремум. Поэтому иногда при оптимизации изменяют величину шага в зависимости от близости к экстремальной точки. Примером такого движения является метод Кифера-Вольфовица.

Метод Кифера-Вольфовица. Характерной чертой этого метода является зависимость пробного и рабочего шагов от номера шага h или от расстояния от оптимума (рис. 6).

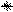
Так размер рабочего шага p=p₀/(hγ), где p₀ – некоторая постоянная, а γ; определяется предполагаемым видом поверхности отклика 0< γ;<0,5; обычно γ;=0,25.

Алгоритм движения к экстремуму по методу Кифера-Вольфовица такой же, как и в методе градиента.

Поскольку градиент определяет направление быстрейшего изменения функции, то методы, базирующиеся на таком методе выбора направления движения, должны быстрее приближаться к экстремуму, однако имеются некоторые трудности, ограничивающие их применение. Так, эти методы предполагают наличие частной производной исследуемой неизвестной функции во всех точках, что практически не всегда возможно. А также определение градиента происходит на каждом шаге, что очень трудоемко.

Метод крутого восхождения. Этот метод объединяет характерные элементы методов Гаусса-Зайделя и градиента. Так, шаговое движение при оптимизации методом крутого восхождения осуществляется в направлении наибольшего изменения функции, то есть в направлении градиента, но в отличии от градиентного метода корректировка направления движения производится не после каждого шага, а после достижения частного экстремума целевой функции (рис. 7), как это делается в методе Гаусса-Зайделя.

 

 

Практически поиск оптимума методом крутого восхождения выполняется по следующему плану:

1. Вблизи исходной точки x₀ проводится эксперимент для определения grad Y (X). Результаты эксперимента подвергаются статистическому анализу и определяются коэффициенты a_i уравнения линейной аппроксимации

2. Вычисляются произведения a_i Δ X_i, где Δ X_i – интервал варьирования фактора X_i при исследовании поверхности отклика в окрестности исходной точки, то есть при определении коэффициента a_i. Фактор, для которого произведение a_i Δ X_i будет максимальным, принимается за базовый (a_б Δ X_б).

3. Для базового фактора выбирается шаг варьирования при движении по направлению к экстремуму λ _б. После этого вычисляются размеры шагов по остальным переменным (λ _i) процесса. Так как при движении к экстремуму по градиенту все исследуемые факторы должны изменятся пропорционально коэффициентам наклона поверхности отклика a_i, то

,

при этом a_i берется со своим знаком.

4. Производятся так называемые «мысленные опыты», которые заключаются в вычислении предсказанных значений функции отклика в точках факторного пространства, лежащих на пути к экстремуму от исходной точки. Таким образом, осуществляется мысленное движение по градиенту к оптимуму в соответствии с математической моделью. при этом i -я координата h -ой точки на этом пути будет:

Отсюда прогнозируемое значение выходного параметра

5. Некоторые из «мысленных опытов» (обычно через 2..5) реализуются, что бы проверить соответствие аппроксимации процесса найденной зависимостью. Наблюдаемые значения сравниваются с предсказанными; точка где в реальном опыте получено наиболее благоприятное минимальное значение выходного параметра принимается за новую начальную точку следующей серии опытов, поставленных аналогичным образом.

6. Поскольку каждый цикл крутого восхождения приближает нас к экстремуму, где крутизна поверхности отклика больше, рекомендуется выбирать шаг для каждой следующей серии опытов равным или меньшим, чем в предыдущей.

7. Эксперимент прекращается, когда все или почти все коэффициенты a_i уравнения получаются незначимыми или равными нулю. Это говорит о выходе в оптимальную область целевой функции (область главного экстремума).

При исследовании сложных объектов данный метод является одним из наиболее эффективных. Он позволяет, с одной стороны, достаточно быстро достичь экстремума, а с другой, – определить характер и силу влияния тех или иных факторов, то есть этот метод позволяет не только оптимизировать процесс, но и исследовать его.

Симплексный метод. Симплексом называется K -мерный выпуклый многогранник, имеющий K +1 вершин. Симплекс называется регулярным, если все расстояния между его вершинами равны. Симплексом нулевой размерности является точка, одномерным симплексом – отрезок прямой, двумерным – треугольник, трехмерным – тетраэдр и так далее.

Во всех рассмотренных ранее методах оптимизации можно выделить пробные эксперименты, предназначенные для определения направления движения, и рабочие шаги, выполняющие продвижение к экстремуму. Особенностью симплексного метода является совмещение процессов изучения поверхности отклика и продвижения по ней к экстремуму. Это достигается тем, что эксперименты ставятся в точках факторного пространства, соответствующим вершинам симплексов.

Действительно, после проведения исходной серии опытов, поставленных в вершинах регулярного K -мерного симплекса выявляется точка, соответствующая условиям, при которых получаются наихудшие результаты. Далее используется важное свойство симплекса, по которому из любого симплекса можно, отбросив одну из вершин, получить новый, заменив отброшенную вершину её зеркальным отражением относительно противоположной его грани (гранью называют совокупность K точек K мерного пространства). Если теперь отбросить точку с наихудшими результатами и построить на оставшейся грани новый симплекс, то очевидно, что центр нового симплекса сместится в направлении экстремума (рис. 8). Затем процесс отбрасывания вершины с наихудшим значением целевой функции и построения нового симплекса повторяется. Если значение выхода в новой точке снова окажется наихудшим, то нужно вернуться к исходному симплексу и отбросить следующую по порядку вершину с плохим результатом. В
результате этого образуется цепочка симплексов, перемещающихся в факторном пространстве к точке экстремума.

Условия проведения опыта в отраженной точке определяются выражением:

где i =1,2,… K;

x_нi – i -ая координата точки наихудшими результатами;

x_0i – i -ая координата центра противоположной грани, которая в свою очередь определяется по формуле:

x _{( K+ 2) i} – i -ая координата новой точки, получаемой в результате зеркального отражения точки с наихудшими результатами.

Показателем выхода в район экстремума служит прекращение поступательного движения симплекса и начало вращения его вокруг одной из вершин, то есть одна и та же точка последовательно встречается более чем в (K +1) симплексах. Следует подчеркнуть, что направление движения к оптимуму, определяемое с помощью симплекса, является в общем случае не самым крутым, траектория движения в этом случае представляет собой ломаную линию, колеблющуюся около линии наиболее крутого восхождения.
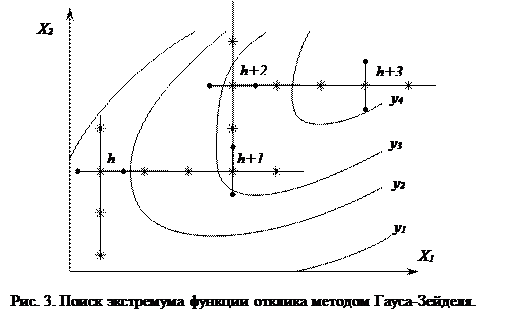
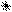
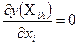
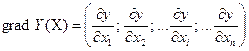
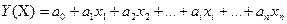
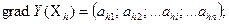
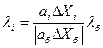