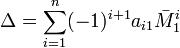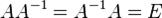Операции с блочными матрицами1. При сложении блочных матриц нужно, чтобы подматрицы были одного размера. 2. При умножении блочной матрицы на число a каждая подматрица умножается на a. 3. При перемножении блочных матриц необходимо согласовать размеры подматриц. 4. При транспонировании блоки на главной диагонали транспонируются и остаются на месте, остальные блоки меняются местами и транспонируются.
6. Определители второго и третьего порядков
Метод Гаусса, рассмотренный выше, весьма прост, состоит из однотипных вычислений и не требует больших усилий при алгоритмической реализации. Однако его существенным недостатком является то, что он не дает возможность сформулировать условия совместности или определенности системы по информации о коэффициентах и свободных членах этой системы. С другой стороны, даже при условии определенности системы этот метод не позволяет построить формулы, выражающие решение системы через ее коэффициенты и свободные члены. Все это, однако, оказывается необходимым при решении различных теоретических вопросов, в частности в геометрических исследованиях. Поэтому теорию систем линейных алгебраических уравнений приходится развивать иными, более глубокими методами.
Сначала рассмотрим частный случай определенных систем, имеющих равное число уравнений и неизвестных.
Пусть дана система двух линейных уравнений с двумя неизвестными
коэффициенты которого составляют квадратную матрицу второго порядка
Применяя к системе (1) метод уравнивания коэффициентов (первое уравнение умножаем на a22, а второе – на a12 и получаем выражение для x1, аналогично – для x2) получим:
предположим, что a11a22 – a12a21¹0. Тогда
Общий знаменатель значений неизвестных (3) легко выражается через элементы матрицы (2): он равен произведению элементов главной диагонали минус произведение элементов второй диагонали. Это число называется определителем или детерминантом матрицы (2), причем, как говорят, определителем второго порядка, т. к. матрица (2) есть матрица второго порядка. Для обозначения определителя матрицы (2) употребляется следующий символ:
Произведения а11 а22 - а12 а21 называются членами определителя второго порядка.
Итак, матрица есть таблица чисел, а определитель – число, соответствующее матрице.
Примеры:
1)
Числитель выражений (3) имеет такой же вид, как и знаменатель, т. е. это тоже знаменатель второго порядка. Числитель выражения для x1 есть определитель матрицы, получающейся из матрицы (2) заменой ее первого столбца столбцом из свободных членов системы (1), а числитель выражения для x2 есть определитель матрицы, получающейся из матрицы (2) такой же заменой ее второго столбца. Таким образом, формулы (3) в новых обозначениях записываются в следующем виде:
Это и есть правило Крамера решения системы двух линейных уравнений с двумя неизвестными: Если определитель (4) из коэффициентов системы уравнений (1) отличен от нуля, то получаем решение системы (1), беря в качестве значений для неизвестных дроби, общим знаменателем которых служит определитель (4) матрицы коэффициентов системы (1), а числителем для неизвестного хi (i=1,2) является определитель, получающийся заменой в определителе (4) i-го столбца (т. е. столбца коэффициентов при неизвестном) столбцом из свободных членов системы (1).
Пример:
Определитель из коэффициентов есть
Он отличен от нуля, и поэтому к системе применимо правило Крамера. Числителями для неизвестных будут определители
Таким образом, решением системы служит следующая пара чисел:
Введение определителей второго порядка не вносит существенных упрощений в решение систем двух линейных уравнений с двумя неизвестными, и без того не представляющее никаких трудностей. Однако, уже для случая трех уравнений с тремя неизвестными аналогичные методы становятся практически полезными.
Пусть дана система
с квадратной матрицей из коэффициентов
Если мы умножим обе части первого из уравнений (6) на число а22а33 - а23а32, обе части второго – на а13а32 - а12а33, обе части третьего – на а12а23 - а13а22, а затем сложим все три уравнения, то, как легко проверить, коэффициенты при х2 и х3 окажутся равными нулю, т. е. эти неизвестные одновременно исключаются, и мы получим равенство:
(a11a22a33+ a12a23a31+ a13a21a32- a13a22a31- a12a21a33- a11a23a32)х1=
= b1a22a33+ a12a23b3+ a13b2a32- a13a22b3- a12b2a33- b1a23a32 (8)
Коэффициенты при х1 в этом равенстве называются определителем третьего порядка, соответствующим матрице (7). Для его записи употребляется такая же символика, как и в случае определителя второго порядка:
Хотя выражение определителя третьего порядка выглядит весьма громоздким, закон его составления из элементов матрицы (7) оказывается довольно простым. В самом деле, один из трех членов определителя, входящих со знаком «плюс» есть произведение элементов главной диагонали, каждый из двух других – произведением элементов, лежащих на параллели к этой диагонали с добавлением третьего множителя из противоположного угла матрицы. Члены, входящие в (9) со знаком «минус» строятся также, но относительно второй диагонали. На рис. 1 слева указано правило вычисления положительных членов определителя третьего порядка, а справа – правило вычисления отрицательных членов. Это правило называется правилом Саррюса.
Шесть основных свойств определителя 3-го порядка.
Определители третьего порядка (как и определители 2-го порядка) обладают следующими шестью свойствами, следующими из формулы (9) (для определителей второго порядка – из формулы (4)).
1. определитель не изменится, если строки его матрицы сделать столбцами, а столбцы строками;
2. при перестановке двух строк определителя он меняет знак;
3. если в определителе имеются две одинаковые строки, то определитель равен нулю;
4. общий множитель определителя строки можно вынести за знак определителя;
5. если элементы одной строки определителя пропорциональны элементам другой, то определитель равен нулю;
6. если к одной строке определителя прибавить другую, умноженную на любое число, то определитель не изменится.
Примеры:
1)
2)
= -20 + 15 +4 = - 1
Правая часть равенства (8) также будет определителем третьего порядка, а именно определителем матрицы, получающейся из матрицы (7) заменой ее первого столбца столбцом из свободных членов системы (6). Обозначим определитель (9) символом D, а определитель матрицы, получающейся заменой j-го столбца столбцом из свободных членов системы (6) символом D1. Тогда равенство (8) приобретает вид D×x1=D1, откуда при D¹0 следует
Таким же путем, умножая уравнения (6) соответственно на числа а23а31 – а21а33, а11а33 – а13а31, а13а21 – а11а23, получим для х2 следующее выражение (снова при d¹0):
Наконец, умножая уравнения (6) соответственно на а21а32 – а22а31, а12а31 – а11а32, а11а22 – а12а21, придем к выражению для х3:
Таким образом, если определитель из коэффициентов системы трех линейных уравнений с тремя неизвестными отличен от нуля, то решение этой системы может быть найдено по правилу Крамера, формулируемому также, как и в случае системы двух уравнений.
Пример: Решить систему:
Определитель из коэффициентов системы отличен от нуля:
поэтому к системе применимо правило Крамера. Числителями для неизвестных будут определители
т. е. решением системы являются следующие значения хi:
7. Минор
Если номера отмеченных строк совпадают с номерами отмеченных столбцов, то минор называется главным, а если отмечены первые k строк и первые k столбцов ― угловым или ведущим главным.
Дополнительный минор элемента матрицы n-го порядка есть определитель порядка (n-1), соответствующий той матрице, которая получается из матрицы путем вычеркивания i-ой строки и j-го столбца.
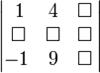
Базисным минором матрицы называется любой её ненулевой минор максимального порядка. Для того чтобы минор был базисным, необходимо и достаточно, чтобы все окаймляющие его миноры (то есть содержащие его миноры на единицу большего порядка) были равны нулю. Система строк (столбцов) матрицы, связанных с базисным минором, является максимальной линейно независимой подсистемой системы всех строк (столбцов) матрицы. Пример Например, есть матрица:
Предположим, надо найти дополнительный минор. Этот минор — определитель матрицы, получающейся путем вычеркивания строки 2 и столбца 3:
Получаем
8. Алгебраические дополнения:
Алгебраическим дополнением элемента аij называется его минор, взятый со знаком "+", если сумма (i + j) четное число, и со знаком "-", если эта сумма нечетное число. Обозначается Аij. Аij = (-1)i+j × Мij.
Тогда можно переформулировать изложенное выше свойство. Определитель матрицы равен сумме произведение элементов некторого ряда (строки или столбца) матрицы на соответствующие им алгебраические дополнения. Пример:
9. Определение через разложение по первой строке
Схема расчета определителя матрицы.
Для матрицы первого порядка детерминантом является сам единственный элемент этой матрицы:
Для матрицы
Для матрицы
В частности, формула вычисления определителя матрицы
Легко доказать, что при транспонировании определитель матрицы не изменяется (иными словами, аналогичное разложение по первому столбцу также справедливо, то есть даёт такой же результат, как и разложение по первой строке):
10. Основные свойства определителей Прежде всего отметим, что det[A] = det[A]t, т. е. определитель матрицы не изменяет своего значения при взаимной замене ее строк и столбцов. Поэтому все свойства определителя, сформулированные для столбцов, справедливы и для строк, и обратно.
Ниже приводятся основные свойства определителей, которые легко доказываются на основе общего выражения (1).
1. При перестановке двух столбцов определитель меняет знак на противоположный (свойство антисимметрии).
2. Определитель равен нулю, если все элементы какого-нибудь столбца равны нулю или если один из столбцов является линейной комбинацией любых его других столбцов (в частности, определитель, у которого хотя бы два столбца одинаковы, равен нулю).
3. Умножение всех элементов какого-нибудь столбца на скаляр k равнозначно умножению определителя на k (общий множитель элементов строки или столбца можно вынести за знак определителя).
4. Умножение матрицы n-го порядка на скаляр k соответствует умножению ее определителя на kn, т.е. det(k[A]) = kndet[A].
5. Значение определителя не изменится, если к какому-нибудь столбцу прибавить другой столбец, умноженный на скаляр k.
6. Если два определителя одинаковых порядков различаются между собой только элементами j-го столбца, то их сумма равна определителю, элементы j-го столбца которого равны суммам соответствующих элементов j-х столбцов исходных определителей, а остальные элементы те же, что у исходных (свойство линейности).
11. Невырожденные матрицы Пусть А - квадратная матрица n - ого порядка.
Квадратная матрица А называется невырожденной, если определитель матрицы (Δ = det A) не равен нулю (Δ = det A ≠ 0). В противном случае (Δ = 0) матрица А называется вырожденной.
Матрицей, союзной к матрице А, называется матрица
, где Аij - алгебраическое дополнение элемента аij данной матрицы (оно определяется так же, как и алгебраическое дополнение элемента определителя матрицы).
Матрица А-1 называется обратной матрице А, если выполняется условие: А × А-1 = А-1 × А = Е , где Е - единичная матрица того же порядка, что и матрица А. Матрица А-1 имеет те же размеры, что и матрица А.
12. Обра́тная ма́трица — такая матрица A−1, при умножении на которую исходная матрица A даёт в результате единичную матрицу E:
Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует. Однако возможно обобщить это понятие и ввести псевдообратные матрицы, похожие на обратные по многим свойствам.
|

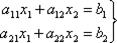 (1)
(1)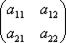 (2)
(2)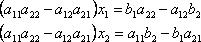
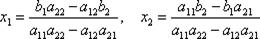 (3)
(3)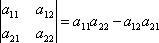 (4)
(4) 2)
2) 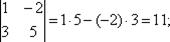
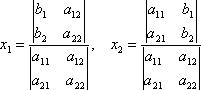 (5)
(5)

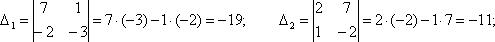
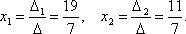
 (6)
(6)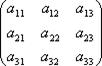 (7)
(7)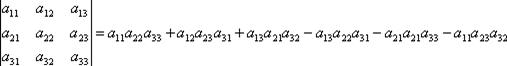 (9)
(9) 2×3×5+1×1×2+2×(-4)×3-2×3×2-1×(-4)×5-2×1×3=30 + 2 – 24 – 12 +20 – 6 =10
2×3×5+1×1×2+2×(-4)×3-2×3×2-1×(-4)×5-2×1×3=30 + 2 – 24 – 12 +20 – 6 =10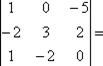 1×3×0+0×2×1+(-5)×(-2)×(-2)-(-5)×3×1-0×(-2)×0-1×2×(-3)=
1×3×0+0×2×1+(-5)×(-2)×(-2)-(-5)×3×1-0×(-2)×0-1×2×(-3)=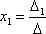 (10)
(10) (11)
(11)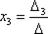 (12)
(12)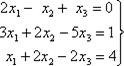



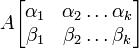 матрицы A ― определитель квадратной матрицы порядка k (который называется также порядком этого минора), элементы которой стоят в матрице A на пересечении строк с номерами
матрицы A ― определитель квадратной матрицы порядка k (который называется также порядком этого минора), элементы которой стоят в матрице A на пересечении строк с номерами 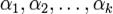 и столбцов с номерами
и столбцов с номерами 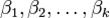 .
.

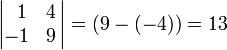
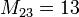
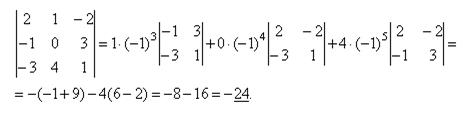
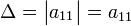
 детерминант определяется как
детерминант определяется как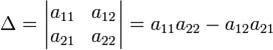
 определитель задаётся рекурсивно:
определитель задаётся рекурсивно: , где
, где 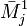 — дополнительный минор к элементу a1j. Эта формула называется разложением по строке.
— дополнительный минор к элементу a1j. Эта формула называется разложением по строке. такова:
такова: = a11a22a33 − a11a23a32 − a12a21a33 + a12a23a31 + a13a21a32 − a13a22a31
= a11a22a33 − a11a23a32 − a12a21a33 + a12a23a31 + a13a21a32 − a13a22a31