Содержание
1. Функция. Основные определения. Последовательность. Предел последовательности 4
2. Предел функции непрерывного аргумента. 12
3. Вычисление пределов функций. Основные приёмы. 18
4. Замечательные пределы. 23
5. Применение эквивалентных бесконечно малых к нахождению пределов функции. Сравнение бесконечно малых. 26
6. Непрерывность функций. Точки разрывa. 31
Список литературы. 35
Функция. Основные определения. Последовательность. Предел последовательности
Если каждому значению переменной х, принадлежащему некоторой области, соответствует одно определенное значение другой переменной у, то у есть функция от х, 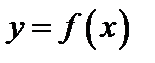 .
.
Переменная х называется независимой переменной или аргументом. Зависимость переменных х и у -функциональная зависимость. Совокупность значений х, для которых определяются значения у в силу  называется областью определения функции (или областью существования). Совокупность всех значений, принимаемых переменной у, называется областью значений функции.
называется областью определения функции (или областью существования). Совокупность всех значений, принимаемых переменной у, называется областью значений функции.
Основные свойства функций:
1. Четность и нечетность. Функция  называется четной, если для любого значения x из области определения
называется четной, если для любого значения x из области определения  и нечетной, еcли для любого значения x из области определения
и нечетной, еcли для любого значения x из области определения 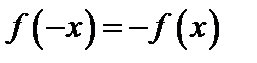 .
.
Например, 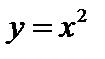 - четная функция, потому что
- четная функция, потому что  , график ее в декартовой системе координат симметричен относительно оси ФОУ;
, график ее в декартовой системе координат симметричен относительно оси ФОУ;
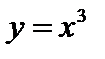 - нечетная функция, потому что
- нечетная функция, потому что 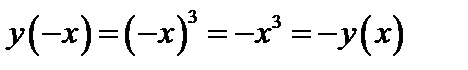 , график ее в декартовой системе координат симметричен относительно точки О(0;0);
, график ее в декартовой системе координат симметричен относительно точки О(0;0);  - не является четной или нечетной,
- не является четной или нечетной,  .
.
2. Монотонность функции. Функция  называется возрастающей, если большему значению аргумента соответствует большее значение функции. Функция
называется возрастающей, если большему значению аргумента соответствует большее значение функции. Функция 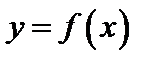 называется убывающей, если большему значению аргумента соответствует меньшее значение функции. Возрастающие или убывающие функции называются монотонными.
называется убывающей, если большему значению аргумента соответствует меньшее значение функции. Возрастающие или убывающие функции называются монотонными.
Для любой монотонной функции 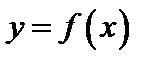 существует обратная функция
существует обратная функция 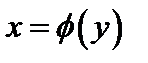 . Значения функции
. Значения функции  для обратной к ней становятся значениями аргумента, а значения аргумента функции
для обратной к ней становятся значениями аргумента, а значения аргумента функции  для обратной к ней становятся значениями функции. График обратной функции в декартовой системе координат симметричен графику данной функции относительно биссектрисы первого координатного угла. Например,
для обратной к ней становятся значениями функции. График обратной функции в декартовой системе координат симметричен графику данной функции относительно биссектрисы первого координатного угла. Например,  и
и 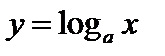 .
.
3. Ограниченность. Функция  называется ограниченной сверху на отрезке
называется ограниченной сверху на отрезке 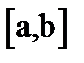 , если существует такое число A, что для всех
, если существует такое число A, что для всех 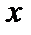
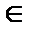
 будет выполняться неравенство
будет выполняться неравенство  <A. Функция
<A. Функция  называется ограниченной снизу на отрезке
называется ограниченной снизу на отрезке 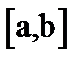 , если существует такое число A, что для всех
, если существует такое число A, что для всех 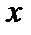
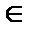
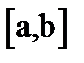 будет выполняться неравенство
будет выполняться неравенство 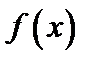 >A. Функция
>A. Функция 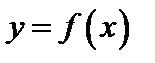 называется ограниченной на отрезке
называется ограниченной на отрезке  , если существует такое положительное число A>0, что для всех
, если существует такое положительное число A>0, что для всех 
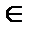
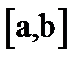 будет выполняться неравенство |
будет выполняться неравенство | 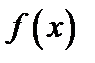 |<A.
|<A.
4. Периодичность. Функция 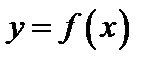 называется периодической, если существует такое число
называется периодической, если существует такое число 
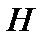 , что для любого значения
, что для любого значения 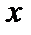 из области определения выполняется равенство
из области определения выполняется равенство  . Период
. Период  - наименьшее положительное число
- наименьшее положительное число  .
.
5. Сложная функция. Пусть у является функцией от u, а u в свою очередь зависит от х, тогда у является функцией от функции или сложной функцией.
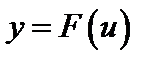 ,
,  .
.
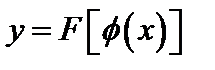
Например,  .
.
Элементарной функцией называется функция, которая может быть задана одной формулой вида 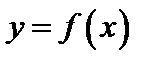 , где справа стоящее выражение составлено из основных элементарных функций и постоянных при помощи конечного числа операций сложения, вычитания, умножения, деления и взятия функции от функции. Основными элементарными функциями являются следующие: степенная, показательная, логарифмическая, тригонометрическая, обратная тригонометрическая.
, где справа стоящее выражение составлено из основных элементарных функций и постоянных при помощи конечного числа операций сложения, вычитания, умножения, деления и взятия функции от функции. Основными элементарными функциями являются следующие: степенная, показательная, логарифмическая, тригонометрическая, обратная тригонометрическая.
Пример 1. Дана функция 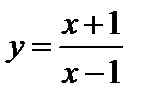 , найти
, найти  ,
, 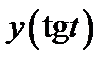 :
:
 ;
; 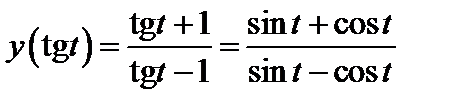
Пример 2. Дана функция: 
Найти y(-1); y(3).
На рис.1 изображен график заданной функции:
Рис 1.
y(-1)=1; y(3)=0
Пример 3. Записать в виде цепочки основных элементарных функций 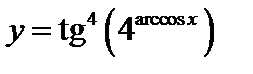 :
:
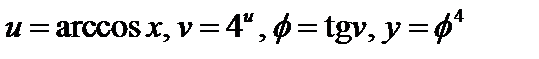 .
.
Пример 4. Найти область определения функции  :
:
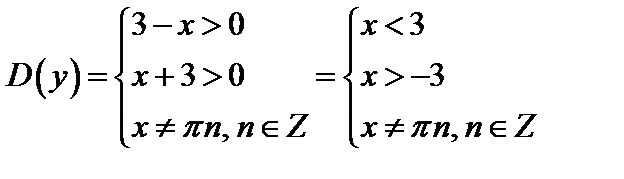
 .
.
Пример 5. Перечислить свойства функции  :
:
четная,  ;
;
ограниченная,  ;
;
периодическая, 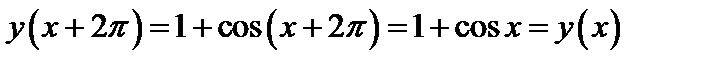 ,
,
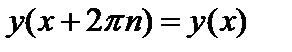 ,
, 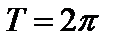 -наименьший период.
-наименьший период.
Последовательность. Предел последовательности
Последовательностью действительных чисел называется функция, определенная на множестве всех натуральных чисел. Число  называется n-м членом последовательности и обозначается символом
называется n-м членом последовательности и обозначается символом  , а формула
, а формула 
 (n) называется формулой общего члена последовательности
(n) называется формулой общего члена последовательности 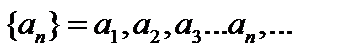
Если для любого n будет выполняться условие  , то последовательность возрастающая; если
, то последовательность возрастающая; если  , то убывающая.
, то убывающая.
Рассмотрим последовательность, заданную 
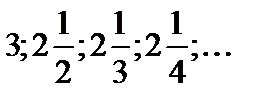
Каждый последующий член этой последовательности меньше предыдущего, это убывающая последовательность.
Число А называется пределом числовой последовательности 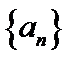 , если для любого сколь угодно малого числа
, если для любого сколь угодно малого числа  найдется такой номер N, что для всех членов последовательности с номерами n>N справедливо неравенство
найдется такой номер N, что для всех членов последовательности с номерами n>N справедливо неравенство
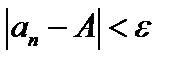 ,
, 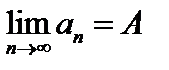
Если последовательность имеет предел, она называется сходящейся, если не имеет – расходящейся.
Пример 6. Написать первые шесть членов последовательности 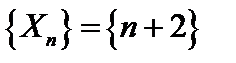

это возрастающая неограниченная последовательность (рис.2).
Рис.2
Пример 7. Написать формулу общего члена последовательности:
 .
.
Ответ: 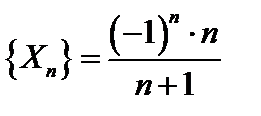 .
.
Пример 8. Используя определение, доказать, что последовательность, заданная формулой 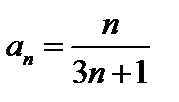 имеет предел, равный
имеет предел, равный  .
.
Чтобы показать, что 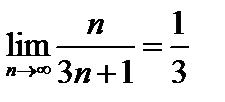 , надо в соответствии с определением по произвольному
, надо в соответствии с определением по произвольному 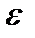 >0 суметь найти такой номер N=N(
>0 суметь найти такой номер N=N(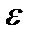 ), чтобы для всех n>N выполнялось неравенство
), чтобы для всех n>N выполнялось неравенство
|  |<
|<  (1),
(1),
преобразуем
|  | <
| < 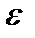 .
.
Так как n-натуральное число, то 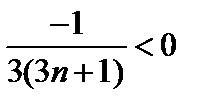 , следовательно
, следовательно
|  |=
|= 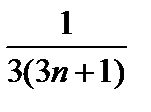 .
.
Таким образом, получаем
 <
<  ,
,
3n+1> 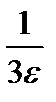 ,
,
3n> 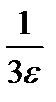 -1,
-1,
n> 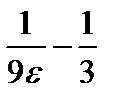 .
.
Следовательно, если положить N( )=[
)=[ 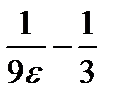 ] ([ ]-целая часть), то при всех n>N неравенство (1) будет выполняться. Таким образом, по произвольно заданному числу
] ([ ]-целая часть), то при всех n>N неравенство (1) будет выполняться. Таким образом, по произвольно заданному числу 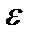 >0 мы можем найти такой номер N=N(
>0 мы можем найти такой номер N=N(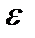 ) (а именно, N=
) (а именно, N= 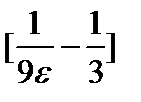 ), что при всех n>N будет выполняться неравенство |
), что при всех n>N будет выполняться неравенство | 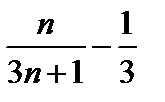 |<
|<  , следовательно, по определению предела
, следовательно, по определению предела 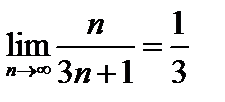 , что и требовалось доказать.
, что и требовалось доказать.
Пример 9. Показать, что при 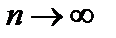 последовательность с общим членом
последовательность с общим членом  имеет пределом число 3/2.
имеет пределом число 3/2.
 ;
; 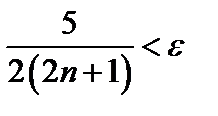 ;
; 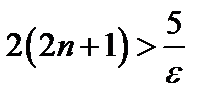 ;
;  .
.
Итак, если 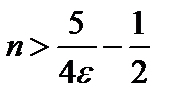 , то
, то  , т.е.
, т.е. 
Полагая 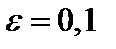 , заключаем, что неравенство
, заключаем, что неравенство 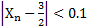 выполняется при
выполняется при 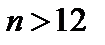 (например, при
(например, при  ). Аналогично, неравенство
). Аналогично, неравенство 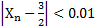 выполняется при
выполняется при 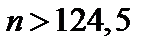 (п=125), а неравенство
(п=125), а неравенство  - при
- при  (п=1250).
(п=1250).
Задания для самостоятельной работы.
№1. Дана функция  . Найти а)
. Найти а) 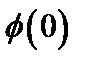 ; б)
; б) 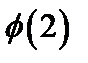 ; в)
; в)  ; г)
; г)  .
.
№2. Дана функция  . Найти а)
. Найти а) 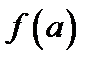 ; б)
; б) 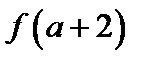 ; в)
; в)  ; г)
; г)  .
.
№3. Дана функция 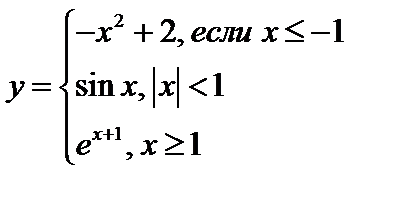 .
.
Найти: а)y(4); б)y(0); в)y(-4).
№4. Записать в виде цепочки основных элементарных функций 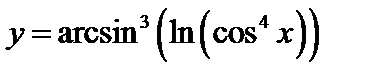 .
.
№5. Записать в виде одной функции цепочку функций 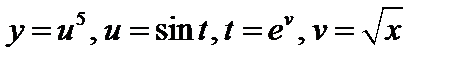 .
.
№6. Найти область определения функций:
а) 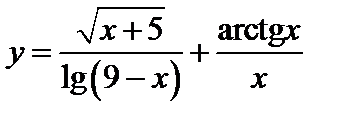 ; б)
; б) 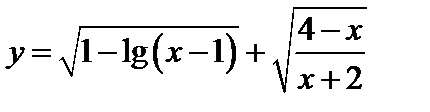 ;
;
в) 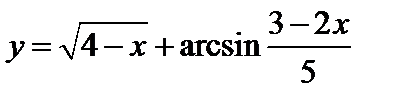 ; г)
; г)  .
.
№7. Перечислить свойства функций:
а)  ; б)
; б)  ;
;
в) 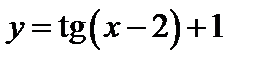 ; г)
; г)  .
.
№8. Написать первые шесть членов последовательностей, изобразить их на чертеже:
а) 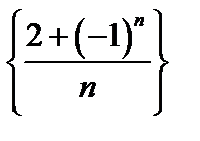 ; б)
; б)  ; в)
; в) 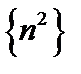 ; г)
; г) 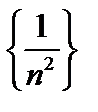 .
.
№9. Написать формулу общего члена последовательности:
а) 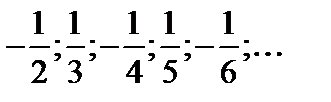 ; б)
; б) 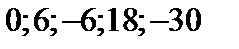 ; в)
; в) 
№10. С помощью определения предела последовательности доказать, что последовательность с общим членом 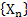 имеет предел а. Найти
имеет предел а. Найти 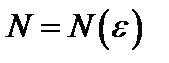 , взяв
, взяв  0,1; 0,01; 0,001; 0,0001, результаты записать в таблицу:
0,1; 0,01; 0,001; 0,0001, результаты записать в таблицу:

| 0,1
| 0,01
| 0,001
| 0,0001
|
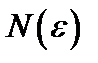
|
|
|
|
|
а)  , а=1.
, а=1.
б) 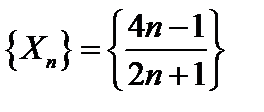 , а=2;
, а=2; 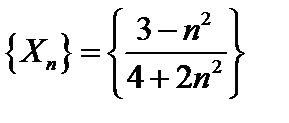 , а
, а  .
.
2. Предел функции непрерывного аргумента
Пусть функция 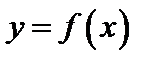 определена в некоторой окрестности точки а или в некоторых точках этой окрестности.
определена в некоторой окрестности точки а или в некоторых точках этой окрестности.
Определение. Функция 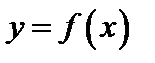 стремится к пределу
стремится к пределу 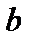 (
(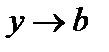 ) при х, стремящемся к
) при х, стремящемся к 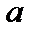 (
( ), если для каждого положительного числа
), если для каждого положительного числа 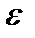 , как бы мало оно ни было, можно указать такое положительное число
, как бы мало оно ни было, можно указать такое положительное число 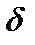 , что для всех х, отличных от а и удовлетворяющих неравенству:
, что для всех х, отличных от а и удовлетворяющих неравенству:  , имеет место неравенство
, имеет место неравенство 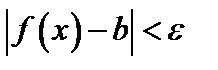
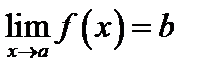
Рис. 3
Так как из неравенства  следует неравенство
следует неравенство 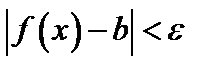 , это значит, что на графике функции
, это значит, что на графике функции  , для всех точек х, отстоящих от точки а не далее чем на
, для всех точек х, отстоящих от точки а не далее чем на 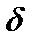 , точки графика М лежат внутри полосы шириной
, точки графика М лежат внутри полосы шириной 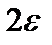 , ограниченной прямыми
, ограниченной прямыми  и
и  .
.
Если  стремится к пределу b1 при х, стремящемся к некоторому числу а так, что х принимает только значения, меньшие а, то пишут
стремится к пределу b1 при х, стремящемся к некоторому числу а так, что х принимает только значения, меньшие а, то пишут  и называют b1 пределом функции
и называют b1 пределом функции 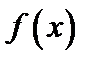 в точке слева.
в точке слева.
Рис. 4
Для существования предела функции при  не требуется, чтобы функция была определена в точке х = а. При нахождении предела рассматриваются значения функции в окрест- ности а.
не требуется, чтобы функция была определена в точке х = а. При нахождении предела рассматриваются значения функции в окрест- ности а.
Функция 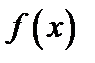 стремится к пределу b при
стремится к пределу b при  , если для каждого произвольно малого положительного числа
, если для каждого произвольно малого положительного числа  можно указать такое положительное число N, что для всех х удовлетворяющих неравенству
можно указать такое положительное число N, что для всех х удовлетворяющих неравенству 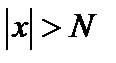 , будет выполняться
, будет выполняться 
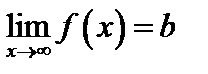
Рис. 5
Пример 1. Докажем, что  . Пусть задано произвольное
. Пусть задано произвольное  , для того чтобы выполнялось неравенство
, для того чтобы выполнялось неравенство 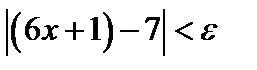 , необходимо выполнение неравенств
, необходимо выполнение неравенств 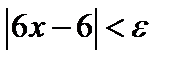 ;
; 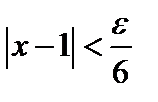 ;
; 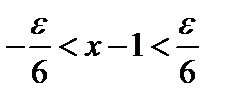 .
.
Таким образом, при любом 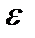 для всех значений х, удовлетворяющих неравенству
для всех значений х, удовлетворяющих неравенству 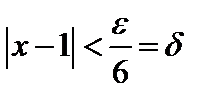 , значение функции 6х+1 будет отличаться от 7 меньше, чем на
, значение функции 6х+1 будет отличаться от 7 меньше, чем на 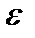 . А это значит, что 7 есть предел функции при
. А это значит, что 7 есть предел функции при 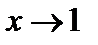 .
.
Пример 2. Докажем, что 
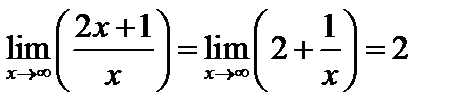
Нужно доказать, что при произвольном 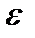 будет выполняться неравенство
будет выполняться неравенство 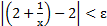 , если только
, если только 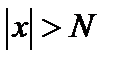 , причем N определяется выбором
, причем N определяется выбором 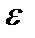 . Данному неравенству эквивалентно следующее:
. Данному неравенству эквивалентно следующее: 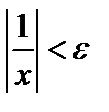 , которое будет выполняться, если будет
, которое будет выполняться, если будет 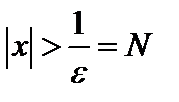 . Это и значит, что
. Это и значит, что  .
.
Функция 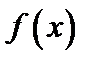 стремится к бесконечности при
стремится к бесконечности при 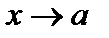 , т.е. является бесконечно большой величиной при
, т.е. является бесконечно большой величиной при 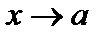 , если для каждого положительного числа М, как бы велико оно ни было, можно найти такое
, если для каждого положительного числа М, как бы велико оно ни было, можно найти такое  , что для всех значений х, отличных от а, удовлетворяющих условию
, что для всех значений х, отличных от а, удовлетворяющих условию 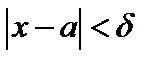 , имеет место неравенство
, имеет место неравенство 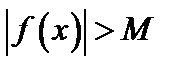 . Тогда пишут:
. Тогда пишут: 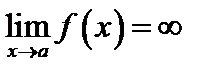 .
.
Если 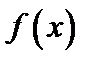 стремится к бесконечности при
стремится к бесконечности при  и при этом принимает только положительные или только отрицательные значения соответственно пишут
и при этом принимает только положительные или только отрицательные значения соответственно пишут  или
или  .
.
Пример 3. Докажем, что 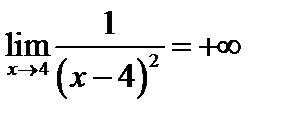
Возьмем произвольное число M>0. Если найдем такое число 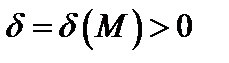 , что для всех х, удовлетворяющих
, что для всех х, удовлетворяющих  , где а=4, будет справедливо неравенство
, где а=4, будет справедливо неравенство  , где
, где 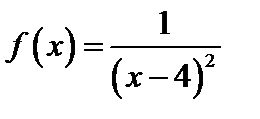 , то утверждение
, то утверждение 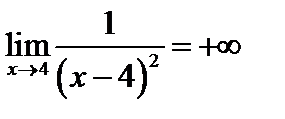 будет доказано.
будет доказано.
 ;
; 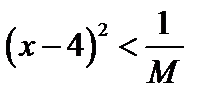 ;
;  .
.
Если положить  и потребовать выполнения неравенства
и потребовать выполнения неравенства
 , то неравенство
, то неравенство  будет справедливо,
будет справедливо,
 .
.
Рис. 6
Геометрически это означает, что для всех  и
и 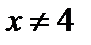 соответствующие точки графика функции
соответствующие точки графика функции 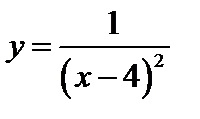 будут находиться выше прямой у = М, т.е. будут находиться в бесконечной полуполосе, ограниченной прямыми
будут находиться выше прямой у = М, т.е. будут находиться в бесконечной полуполосе, ограниченной прямыми  и
и 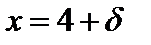 , у = М, причем у>М.
, у = М, причем у>М.
Пример 4. Докажем, что при  функция
функция  предела не имеет.
предела не имеет.
Функция sinx периодическая с периодом 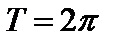 , следовательно, при неограниченном возрастании аргумента эта функция периодически пробегает все свои значения
, следовательно, при неограниченном возрастании аргумента эта функция периодически пробегает все свои значения 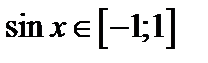 .
.
Но это значит, что при возрастании х значения функции не могут отличаться от любого постоянного числа все менее и менее. Значит функция sinx предела не имеет.
На самом деле, из определения конечного предела вытекает, что если функция имеет конечный предел при  то этот предел один. Следовательно, если взять последовательность точек
то этот предел один. Следовательно, если взять последовательность точек 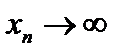 , то соответствующая последовательность значений функции
, то соответствующая последовательность значений функции 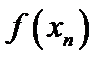 должна иметь предел, равный а.
должна иметь предел, равный а.
Возьмем две последовательности 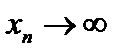 .
.
1)  ;
; 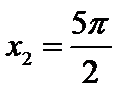 ;
; 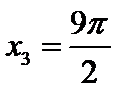 ; …;
; …; 
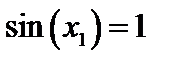 ;
;  ;
;  ; …;
; …; 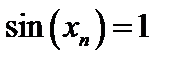 , предел равен а=1.
, предел равен а=1.
2) 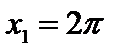 ;
;  ;
; 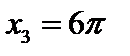 ;…;
;…; 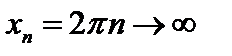
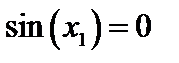 ;
;  ;
;  ; …;
; …; 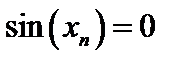 , предел равен а=0.
, предел равен а=0.
Выделение последовательности значений функции sinx при 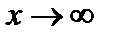 имеют различные пределы, следовательно, данная функция предела не имеет.
имеют различные пределы, следовательно, данная функция предела не имеет.
Задания для самостоятельной работы.
№1 Найти пределы функций или доказать, что они не существуют
а) 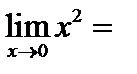 ; б)
; б) 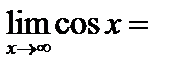 ; в)
; в)  ;
;
г)  ; д)
; д)  ; е)
; е) 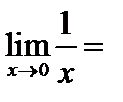
№2 Доказать, что а)  ; б)
; б) 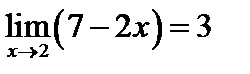
№3 Доказать, что 
№4 Доказать, что 
3. Вычисление пределов функций. Основные приёмы
Основные теоремы о пределах.
Теорема 1. Предел алгебраической суммы двух, трех и вообще определенного числа переменных равен алгебраической сумме пределов этих переменных:
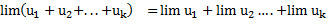
Теорема 2. Предел произведение двух и трех и вообще определенного числа переменных равен произведению пределов этих переменных.

Следствие: Постоянный множитель можно выносить за знак предела.
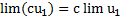
Теорема 3. Предел частного двух переменных равен частному пределов этих переменных, если предел знаменателя отличен от нуля:
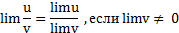
Теорема 4. Если между соответствующими значениями трех функций 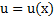 ,
, 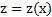 ,
,  выполняются неравенства
выполняются неравенства  ≤
≤  ≤
≤  , при этом функции
, при этом функции 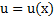 и
и  при
при  (или при
(или при  ) стремятся к одному и тому же пределу b, то
) стремятся к одному и тому же пределу b, то 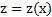 при
при  (или при
(или при  ) стремится к тому же пределу b.
) стремится к тому же пределу b.
Теорема 5. Если при  (или при
(или при  ) функция у принимает неотрицательные значения y ≥ 0 и при этом стремится к пределу b, то b есть неотрицательное число (b ≥0).
) функция у принимает неотрицательные значения y ≥ 0 и при этом стремится к пределу b, то b есть неотрицательное число (b ≥0).
Теорема 6. Если между соответствующими значениями двух функций 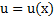 и
и  , стремящихся к пределам при
, стремящихся к пределам при  (или при
(или при  ), выполняется неравенство
), выполняется неравенство  ≥
≥  , то имеет место
, то имеет место 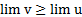 .
.
Теорема 7. Если переменная величина  возрастает, т.е. всякое ее последующее значение больше предыдущего, и если она ограничена, т.е.
возрастает, т.е. всякое ее последующее значение больше предыдущего, и если она ограничена, т.е.  <M, то эта переменная величина имеет предел
<M, то эта переменная величина имеет предел
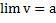 , где
, где 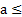 M.
M.
Пример 1. Найти предел  , применяя теоремы о пределах
, применяя теоремы о пределах
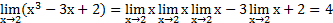
Пример 2. Найти предел 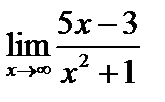
Чтобы раскрыть неопределенность 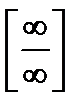 следует числитель и знаменатель поделить почленно на переменную в высшей степени (высшего порядка), стоящую в знаменателе.
следует числитель и знаменатель поделить почленно на переменную в высшей степени (высшего порядка), стоящую в знаменателе.
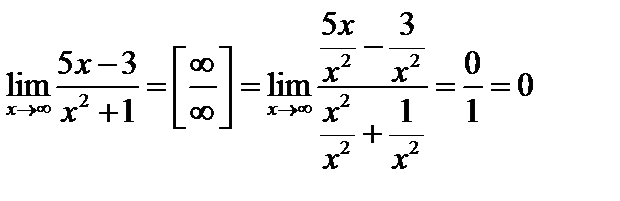
Пример 3. Найти предел 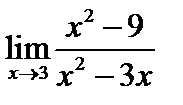
Чтобы раскрыть неопределенность 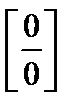 - при случае х→а отношения двух многочленов, следует в числителе и знаменателе дроби выделить общий множитель вида (х - а) и на него сократить, т.к. под знаком предела х → а, но никогда его не достигает.
- при случае х→а отношения двух многочленов, следует в числителе и знаменателе дроби выделить общий множитель вида (х - а) и на него сократить, т.к. под знаком предела х → а, но никогда его не достигает.
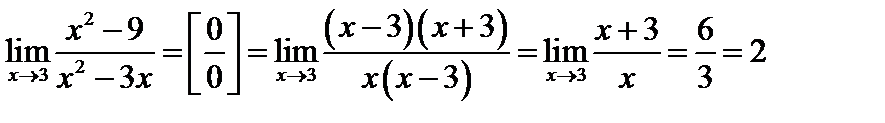 .
.
Пример 4. Найти предел 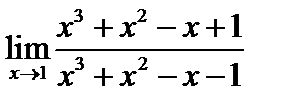 .
.

Пример 5. Найти предел 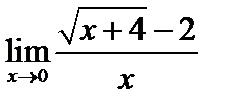 .
.
Чтобы раскрыть неопределенность  при х → а в случае отношения иррациональных функций, следует начать с умножения на выражение, сопряженное данному иррациональному, с целью последующего выделения общего множителя (х - а) и сокращения,
при х → а в случае отношения иррациональных функций, следует начать с умножения на выражение, сопряженное данному иррациональному, с целью последующего выделения общего множителя (х - а) и сокращения,
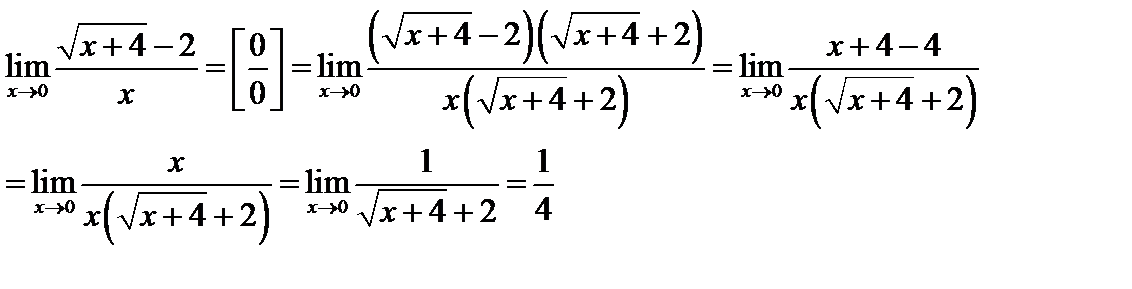
Пример 6. Найти предел 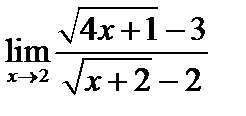 .
.
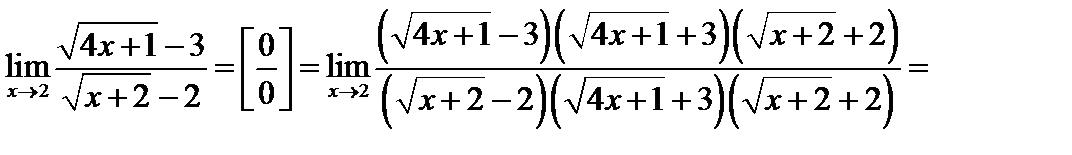

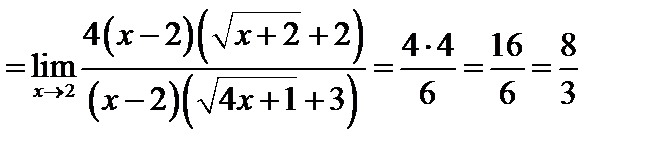
Пример 7. Найти предел  .
.
Чтобы разрешить неопределенность 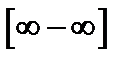 в данном случае, следует привести выражение к общему знаменателю.
в данном случае, следует привести выражение к общему знаменателю.

Пример 8. Найти предел 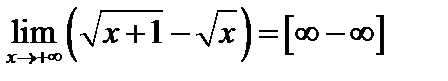
Чтобы разрешить неопределенность 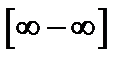 в данном случае, следует домножить и разделить на сопряженное выражение.
в данном случае, следует домножить и разделить на сопряженное выражение.

Задания для самостоятельной работы
Найти пределы:
1) 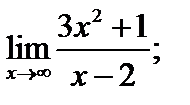 2)
2) 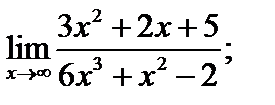 3)
3) 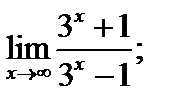
4) 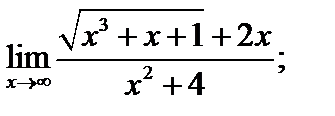 5)
5) 
6) 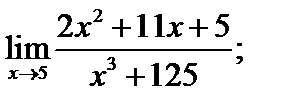 7)
7) 
8)  9)
9)  ;
;
10)  ; 11)
; 11) 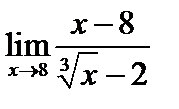 ;
;
12) 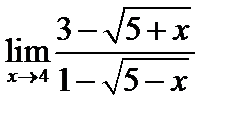 ; 13)
; 13)  ;
;
14)  ; 15)
; 15) 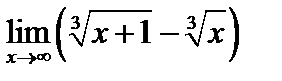

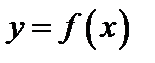 .
. называется областью определения функции (или областью существования). Совокупность всех значений, принимаемых переменной у, называется областью значений функции.
называется областью определения функции (или областью существования). Совокупность всех значений, принимаемых переменной у, называется областью значений функции. называется четной, если для любого значения x из области определения
называется четной, если для любого значения x из области определения  и нечетной, еcли для любого значения x из области определения
и нечетной, еcли для любого значения x из области определения 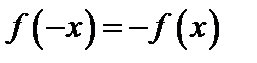 .
.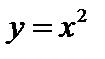 - четная функция, потому что
- четная функция, потому что  , график ее в декартовой системе координат симметричен относительно оси ФОУ;
, график ее в декартовой системе координат симметричен относительно оси ФОУ;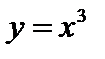 - нечетная функция, потому что
- нечетная функция, потому что 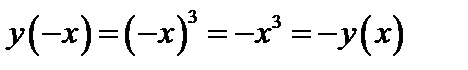 , график ее в декартовой системе координат симметричен относительно точки О(0;0);
, график ее в декартовой системе координат симметричен относительно точки О(0;0);  - не является четной или нечетной,
- не является четной или нечетной,  .
. называется возрастающей, если большему значению аргумента соответствует большее значение функции. Функция
называется возрастающей, если большему значению аргумента соответствует большее значение функции. Функция 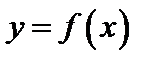 называется убывающей, если большему значению аргумента соответствует меньшее значение функции. Возрастающие или убывающие функции называются монотонными.
называется убывающей, если большему значению аргумента соответствует меньшее значение функции. Возрастающие или убывающие функции называются монотонными.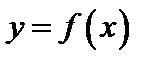 существует обратная функция
существует обратная функция 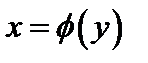 . Значения функции
. Значения функции  для обратной к ней становятся значениями аргумента, а значения аргумента функции
для обратной к ней становятся значениями аргумента, а значения аргумента функции  для обратной к ней становятся значениями функции. График обратной функции в декартовой системе координат симметричен графику данной функции относительно биссектрисы первого координатного угла. Например,
для обратной к ней становятся значениями функции. График обратной функции в декартовой системе координат симметричен графику данной функции относительно биссектрисы первого координатного угла. Например,  и
и 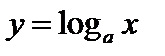 .
. называется ограниченной сверху на отрезке
называется ограниченной сверху на отрезке 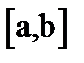 , если существует такое число A, что для всех
, если существует такое число A, что для всех 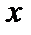
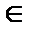
 будет выполняться неравенство
будет выполняться неравенство  <A. Функция
<A. Функция  называется ограниченной снизу на отрезке
называется ограниченной снизу на отрезке 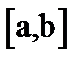 , если существует такое число A, что для всех
, если существует такое число A, что для всех 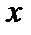
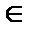
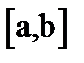 будет выполняться неравенство
будет выполняться неравенство 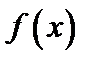 >A. Функция
>A. Функция 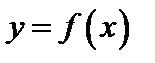 называется ограниченной на отрезке
называется ограниченной на отрезке  , если существует такое положительное число A>0, что для всех
, если существует такое положительное число A>0, что для всех 
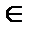
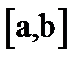 будет выполняться неравенство |
будет выполняться неравенство | 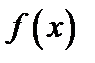 |<A.
|<A.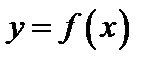 называется периодической, если существует такое число
называется периодической, если существует такое число 
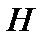 , что для любого значения
, что для любого значения 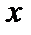 из области определения выполняется равенство
из области определения выполняется равенство  . Период
. Период  - наименьшее положительное число
- наименьшее положительное число  .
.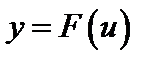 ,
,  .
.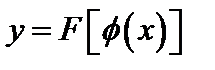
 .
.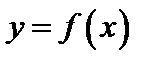 , где справа стоящее выражение составлено из основных элементарных функций и постоянных при помощи конечного числа операций сложения, вычитания, умножения, деления и взятия функции от функции. Основными элементарными функциями являются следующие: степенная, показательная, логарифмическая, тригонометрическая, обратная тригонометрическая.
, где справа стоящее выражение составлено из основных элементарных функций и постоянных при помощи конечного числа операций сложения, вычитания, умножения, деления и взятия функции от функции. Основными элементарными функциями являются следующие: степенная, показательная, логарифмическая, тригонометрическая, обратная тригонометрическая.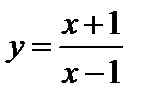 , найти
, найти  ,
, 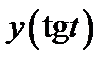 :
: ;
; 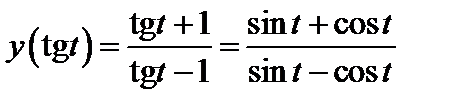

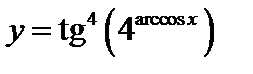 :
: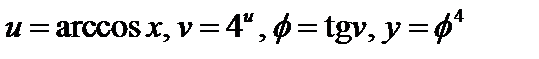 .
. :
: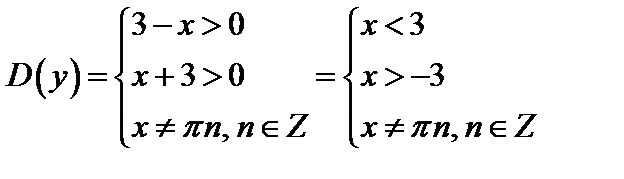
 .
. :
: ;
; ;
;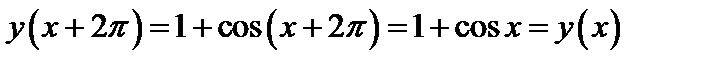 ,
,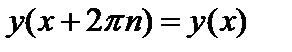 ,
, 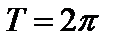 -наименьший период.
-наименьший период. называется n-м членом последовательности и обозначается символом
называется n-м членом последовательности и обозначается символом  , а формула
, а формула 
 (n) называется формулой общего члена последовательности
(n) называется формулой общего члена последовательности 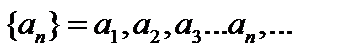
 , то последовательность возрастающая; если
, то последовательность возрастающая; если  , то убывающая.
, то убывающая.
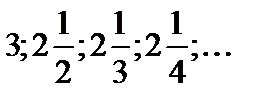
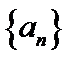 , если для любого сколь угодно малого числа
, если для любого сколь угодно малого числа  найдется такой номер N, что для всех членов последовательности с номерами n>N справедливо неравенство
найдется такой номер N, что для всех членов последовательности с номерами n>N справедливо неравенство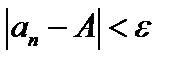 ,
, 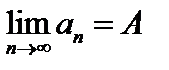
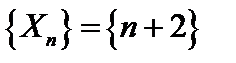

 .
.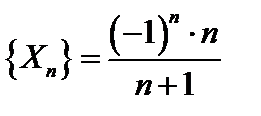 .
.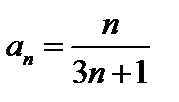 имеет предел, равный
имеет предел, равный  .
.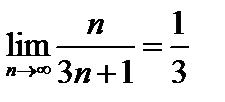 , надо в соответствии с определением по произвольному
, надо в соответствии с определением по произвольному 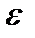 >0 суметь найти такой номер N=N(
>0 суметь найти такой номер N=N(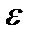 ), чтобы для всех n>N выполнялось неравенство
), чтобы для всех n>N выполнялось неравенство |<
|<  (1),
(1), | <
| < 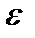 .
.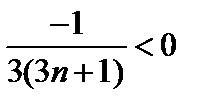 , следовательно
, следовательно |=
|= 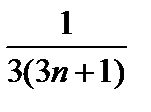 .
. <
<  ,
,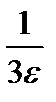 ,
,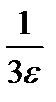 -1,
-1,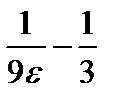 .
. )=[
)=[ 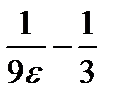 ] ([ ]-целая часть), то при всех n>N неравенство (1) будет выполняться. Таким образом, по произвольно заданному числу
] ([ ]-целая часть), то при всех n>N неравенство (1) будет выполняться. Таким образом, по произвольно заданному числу 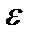 >0 мы можем найти такой номер N=N(
>0 мы можем найти такой номер N=N(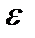 ) (а именно, N=
) (а именно, N= 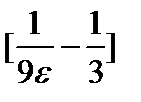 ), что при всех n>N будет выполняться неравенство |
), что при всех n>N будет выполняться неравенство | 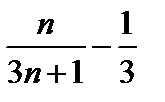 |<
|<  , следовательно, по определению предела
, следовательно, по определению предела 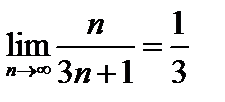 , что и требовалось доказать.
, что и требовалось доказать.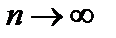 последовательность с общим членом
последовательность с общим членом  имеет пределом число 3/2.
имеет пределом число 3/2. ;
; 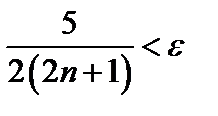 ;
; 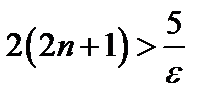 ;
;  .
.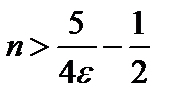 , то
, то  , т.е.
, т.е. 
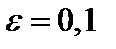 , заключаем, что неравенство
, заключаем, что неравенство 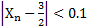 выполняется при
выполняется при 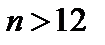 (например, при
(например, при  ). Аналогично, неравенство
). Аналогично, неравенство 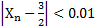 выполняется при
выполняется при 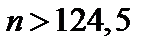 (п=125), а неравенство
(п=125), а неравенство  - при
- при  (п=1250).
(п=1250). . Найти а)
. Найти а) 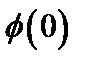 ; б)
; б) 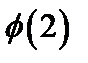 ; в)
; в)  ; г)
; г)  .
. . Найти а)
. Найти а) 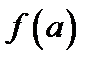 ; б)
; б) 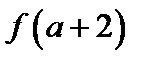 ; в)
; в)  ; г)
; г)  .
.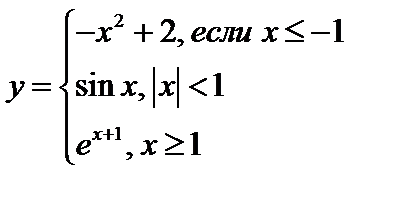 .
.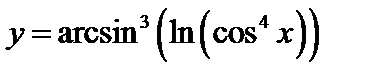 .
.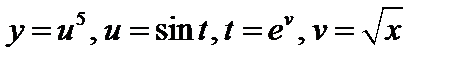 .
.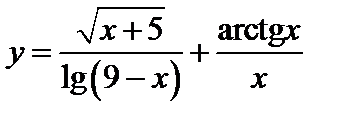 ; б)
; б) 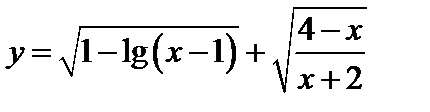 ;
;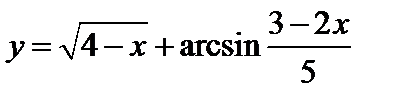 ; г)
; г)  .
. ; б)
; б)  ;
;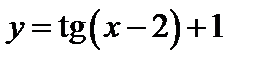 ; г)
; г)  .
.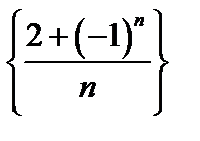 ; б)
; б)  ; в)
; в) 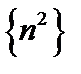 ; г)
; г) 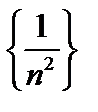 .
.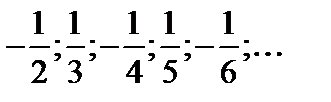 ; б)
; б) 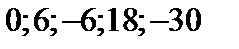 ; в)
; в) 
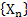 имеет предел а. Найти
имеет предел а. Найти 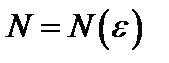 , взяв
, взяв  0,1; 0,01; 0,001; 0,0001, результаты записать в таблицу:
0,1; 0,01; 0,001; 0,0001, результаты записать в таблицу:
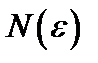
 , а=1.
, а=1.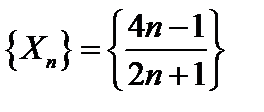 , а=2;
, а=2; 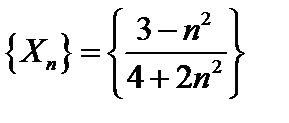 , а
, а  .
.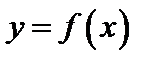 определена в некоторой окрестности точки а или в некоторых точках этой окрестности.
определена в некоторой окрестности точки а или в некоторых точках этой окрестности.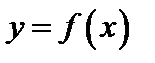 стремится к пределу
стремится к пределу 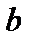 (
(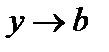 ) при х, стремящемся к
) при х, стремящемся к 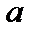 (
( ), если для каждого положительного числа
), если для каждого положительного числа 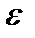 , как бы мало оно ни было, можно указать такое положительное число
, как бы мало оно ни было, можно указать такое положительное число 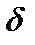 , что для всех х, отличных от а и удовлетворяющих неравенству:
, что для всех х, отличных от а и удовлетворяющих неравенству:  , имеет место неравенство
, имеет место неравенство 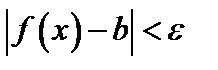
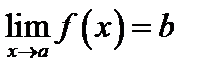
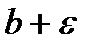



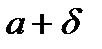

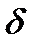

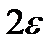
 следует неравенство
следует неравенство 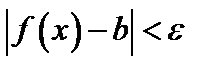 , это значит, что на графике функции
, это значит, что на графике функции  , для всех точек х, отстоящих от точки а не далее чем на
, для всех точек х, отстоящих от точки а не далее чем на 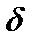 , точки графика М лежат внутри полосы шириной
, точки графика М лежат внутри полосы шириной 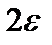 , ограниченной прямыми
, ограниченной прямыми  и
и  .
. стремится к пределу b1 при х, стремящемся к некоторому числу а так, что х принимает только значения, меньшие а, то пишут
стремится к пределу b1 при х, стремящемся к некоторому числу а так, что х принимает только значения, меньшие а, то пишут  и называют b1 пределом функции
и называют b1 пределом функции 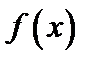 в точке слева.
в точке слева.
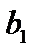
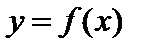
 не требуется, чтобы функция была определена в точке х = а. При нахождении предела рассматриваются значения функции в окрест- ности а.
не требуется, чтобы функция была определена в точке х = а. При нахождении предела рассматриваются значения функции в окрест- ности а.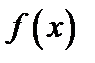 стремится к пределу b при
стремится к пределу b при  , если для каждого произвольно малого положительного числа
, если для каждого произвольно малого положительного числа  можно указать такое положительное число N, что для всех х удовлетворяющих неравенству
можно указать такое положительное число N, что для всех х удовлетворяющих неравенству 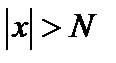 , будет выполняться
, будет выполняться 
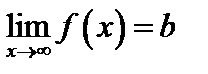
 . Пусть задано произвольное
. Пусть задано произвольное  , для того чтобы выполнялось неравенство
, для того чтобы выполнялось неравенство 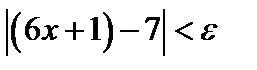 , необходимо выполнение неравенств
, необходимо выполнение неравенств 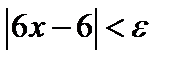 ;
; 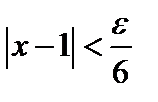 ;
; 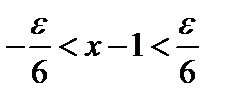 .
.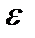 для всех значений х, удовлетворяющих неравенству
для всех значений х, удовлетворяющих неравенству 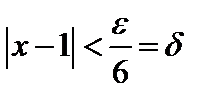 , значение функции 6х+1 будет отличаться от 7 меньше, чем на
, значение функции 6х+1 будет отличаться от 7 меньше, чем на 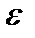 . А это значит, что 7 есть предел функции при
. А это значит, что 7 есть предел функции при 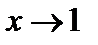 .
.
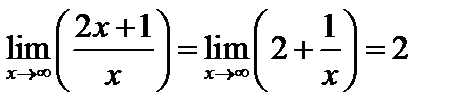
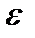 будет выполняться неравенство
будет выполняться неравенство 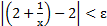 , если только
, если только 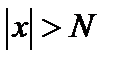 , причем N определяется выбором
, причем N определяется выбором 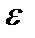 . Данному неравенству эквивалентно следующее:
. Данному неравенству эквивалентно следующее: 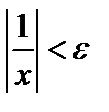 , которое будет выполняться, если будет
, которое будет выполняться, если будет 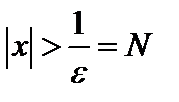 . Это и значит, что
. Это и значит, что  .
.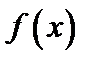 стремится к бесконечности при
стремится к бесконечности при 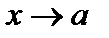 , т.е. является бесконечно большой величиной при
, т.е. является бесконечно большой величиной при 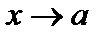 , если для каждого положительного числа М, как бы велико оно ни было, можно найти такое
, если для каждого положительного числа М, как бы велико оно ни было, можно найти такое  , что для всех значений х, отличных от а, удовлетворяющих условию
, что для всех значений х, отличных от а, удовлетворяющих условию 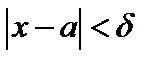 , имеет место неравенство
, имеет место неравенство 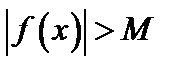 . Тогда пишут:
. Тогда пишут: 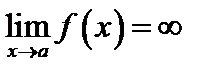 .
.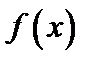 стремится к бесконечности при
стремится к бесконечности при  и при этом принимает только положительные или только отрицательные значения соответственно пишут
и при этом принимает только положительные или только отрицательные значения соответственно пишут  или
или  .
.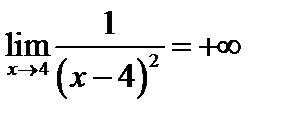
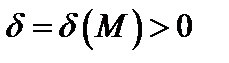 , что для всех х, удовлетворяющих
, что для всех х, удовлетворяющих  , где а=4, будет справедливо неравенство
, где а=4, будет справедливо неравенство  , где
, где 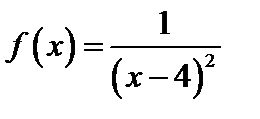 , то утверждение
, то утверждение 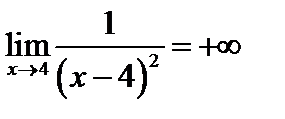 будет доказано.
будет доказано. ;
; 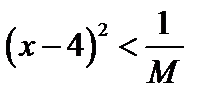 ;
;  .
. и потребовать выполнения неравенства
и потребовать выполнения неравенства , то неравенство
, то неравенство  будет справедливо,
будет справедливо, .
.
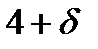
 и
и 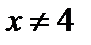 соответствующие точки графика функции
соответствующие точки графика функции 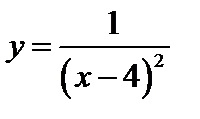 будут находиться выше прямой у = М, т.е. будут находиться в бесконечной полуполосе, ограниченной прямыми
будут находиться выше прямой у = М, т.е. будут находиться в бесконечной полуполосе, ограниченной прямыми  и
и 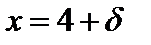 , у = М, причем у>М.
, у = М, причем у>М. функция
функция  предела не имеет.
предела не имеет.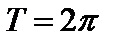 , следовательно, при неограниченном возрастании аргумента эта функция периодически пробегает все свои значения
, следовательно, при неограниченном возрастании аргумента эта функция периодически пробегает все свои значения 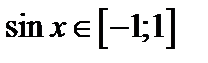 .
. то этот предел один. Следовательно, если взять последовательность точек
то этот предел один. Следовательно, если взять последовательность точек 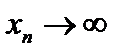 , то соответствующая последовательность значений функции
, то соответствующая последовательность значений функции 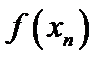 должна иметь предел, равный а.
должна иметь предел, равный а.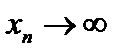 .
. ;
; 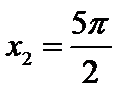 ;
; 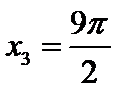 ; …;
; …; 
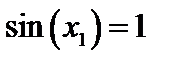 ;
;  ;
;  ; …;
; …; 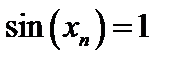 , предел равен а=1.
, предел равен а=1.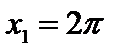 ;
;  ;
; 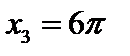 ;…;
;…; 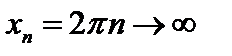
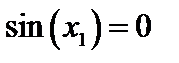 ;
;  ;
;  ; …;
; …; 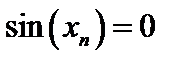 , предел равен а=0.
, предел равен а=0.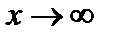 имеют различные пределы, следовательно, данная функция предела не имеет.
имеют различные пределы, следовательно, данная функция предела не имеет.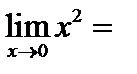 ; б)
; б) 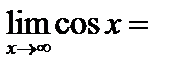 ; в)
; в)  ;
; ; д)
; д)  ; е)
; е) 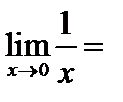
 ; б)
; б) 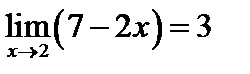


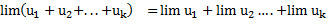

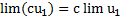
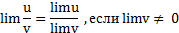
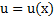 ,
, 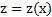 ,
,  выполняются неравенства
выполняются неравенства  ≤
≤  ≤
≤  , при этом функции
, при этом функции  (или при
(или при  ) стремятся к одному и тому же пределу b, то
) стремятся к одному и тому же пределу b, то 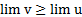 .
.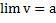 , где
, где 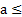 M.
M. , применяя теоремы о пределах
, применяя теоремы о пределах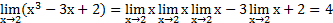
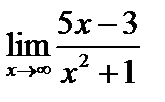
 следует числитель и знаменатель поделить почленно на переменную в высшей степени (высшего порядка), стоящую в знаменателе.
следует числитель и знаменатель поделить почленно на переменную в высшей степени (высшего порядка), стоящую в знаменателе.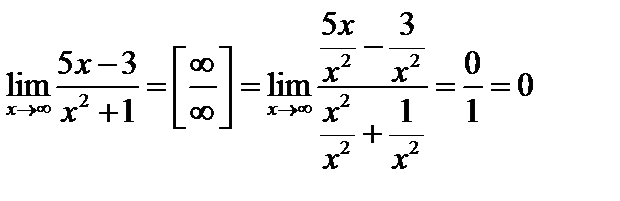
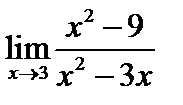
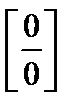 - при случае х→а отношения двух многочленов, следует в числителе и знаменателе дроби выделить общий множитель вида (х - а) и на него сократить, т.к. под знаком предела х → а, но никогда его не достигает.
- при случае х→а отношения двух многочленов, следует в числителе и знаменателе дроби выделить общий множитель вида (х - а) и на него сократить, т.к. под знаком предела х → а, но никогда его не достигает.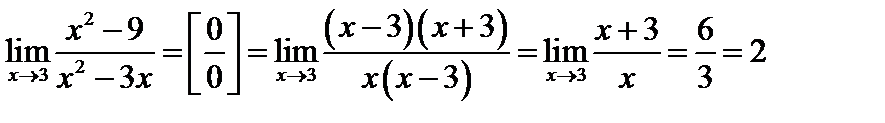 .
.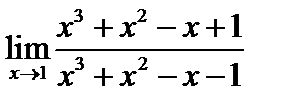 .
.
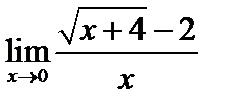 .
. при х → а в случае отношения иррациональных функций, следует начать с умножения на выражение, сопряженное данному иррациональному, с целью последующего выделения общего множителя (х - а) и сокращения,
при х → а в случае отношения иррациональных функций, следует начать с умножения на выражение, сопряженное данному иррациональному, с целью последующего выделения общего множителя (х - а) и сокращения,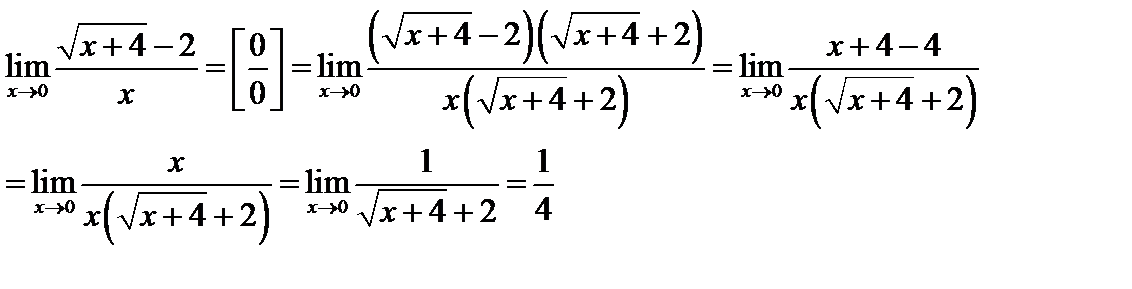
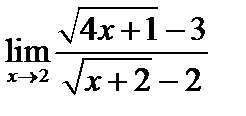 .
.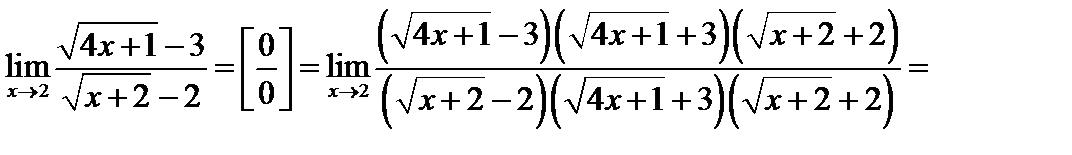

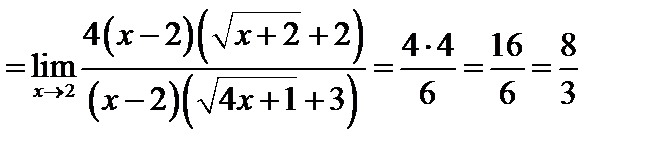
 .
.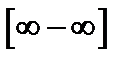 в данном случае, следует привести выражение к общему знаменателю.
в данном случае, следует привести выражение к общему знаменателю.
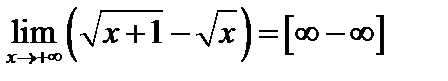
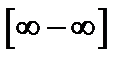 в данном случае, следует домножить и разделить на сопряженное выражение.
в данном случае, следует домножить и разделить на сопряженное выражение.
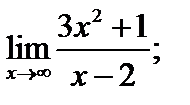 2)
2) 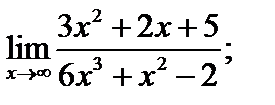 3)
3) 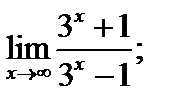
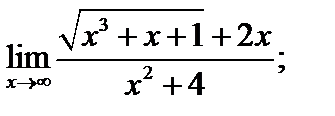 5)
5) 
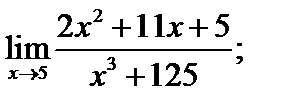 7)
7) 
 9)
9)  ;
; ; 11)
; 11) 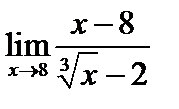 ;
;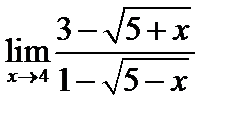 ; 13)
; 13)  ;
; ; 15)
; 15)