Случайное событие, его частота и вероятность
Таблица основных интегралов
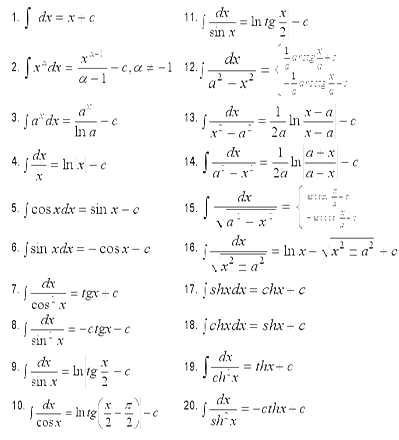
Случайное событие, его частота и вероятность
| Случайными событиями называются такие события, которые могут произойти или не произойти при осуществлении совокупности условий, связанных с возможностью появления данных событий. Случайные события обозначают буквами A, B, C,.... Каждое осуществление рассматриваемой совокупности называется испытанием. Число испытаний может неограниченно возрастать. Отношения числа m наступлений данного случайного события A в данной серии испытаний к общему числу n испытаний этой серии называется частотой появления события A в данной серии испытаний (или просто частотой события А) и обозначается Р*(А). Таким образом, P*(A)=m/n. Частота случайного события всегда заключена между нулем и единицей: 0 ≤ P*(A) ≤ 1. Массовые случайные события обладают свойством устойчивости частоты: наблюдаемые в различных сериях однородных испытаний (с достаточно большим числом испытаний в каждой серии) значения частоты данного случайного события колеблются от серии к серии в довольно тесных пределах. Именно это обстоятельство позволяет при изучении случайных событий применять математические методы, приписывая каждому массовому случайному событию его вероятность, за которую принимается то (вообще говоря заранее неизвестное) число, около которого колеблется наблюдаемая частота события. Вероятность случайного события А обозначается через Р(А). Вероятность случайного события, как и его частота, заключена между нулем и единицей: 0 ≤ P(A) ≤ 1. Достоверному событию (т.е. событию, которое должно произойти при каждом испытании) приписывают вероятность Р(А)=1. Невозможному событию (т.е. событие, которое не может произойти ни при одном испытании) приписывают вероятность Р(А)=0. В некоторых простейших случаях вероятность случайного события может быть определена заранее. Это можно сделать, например, тогда, когда возможные результаты каждого из однородных испытаний могут быть представлены в виде n единственно возможных, несовместных друг с другом и равновозможных исходов ("случаев") (т.е. кроме этих n исходов не может быть никаких других, никакие два из них не могут произойти одновременно и есть основания считать, что любой из них не является более возможным, чем другие). Если из этих n единственно возможных, несовместных и равновозможных случаев m случаев связаны с наступлением события А (или, как говорят в теории вероятностей, "благоприятствуют" А), то за вероятность события А принимается отношение m к n: P(A)=m/n. Задача 1 В ящике 10 перенумерованных шаров с номерами от 1 до 10. Вынули один шар. Какова вероятность того, что номер вынутого шара не превышает 10? Решение. Так как номер любого шара, находящегося в ящике, не превышает 10, то число случаев, благоприятствующих событию А, равно числу всех возможных случаев, т.е. m=n=10 и P(A)=1. В этом случае А достоверно. Задача 2 В урне 15 шаров: 5 белых и 10 черных. Какова вероятность вынуть из урны синий шар? Решение. Синий шаров в урне нет, т.е. m=0, a n=15. Следовательно, P(A)=0/15=0. В данном случае событие А - невозможное. Задача 3 В урне 12 шаров: 3 белых, 4 черных и 5 красных. Какова вероятность вынуть из урны черный шар? Решение. Здесь m=4, n=12 и P(A)=4/12=1/3. Задача 4 В урне 10 шаров: 6 белых и 4 черных. Вынули два шара. Какова вероятность, что оба шара - белые? Решение. Здесь число всех случаев n=C210=(10·9)/(1·2)=45. Число же случаев, благоприятствующих событию А, определяется равенством m=C26 т.е. m=(6·5)/(1·2)=15. Итак, Р(А)=15/45=1/3. Задача 5 В лотерее 2000 билетов. На один билет падает выигрыш 100 руб., на четыре билета - выигрыш по 50 руб., на десять билетов - выигрыш по 20 руб., на двадцать билетов - выигрыш по 10 руб., на 165 билетов - выигрыш по 5 руб., на 400 билетов - выигрыш по 1 руб. Остальные билеты невыигрышные. Какова вероятность выиграть по билету не меньше 10 руб.? Решение. Здесь m=1+4+10+20=35, n=2000, т.е. Р(А)=m/n=35/2000=0,0175.
| Аксиомы сложения и умножения вероятностей
Объединением (или суммой) нескольких случайных событий называется событие, состоящее в осуществлении по крайней мере одного из данных событий. Объединение событий А1, А2,..., Аnобозначается через А1∪ А2∪... ∪ Аn или А1 + А2 +... + Аn. Если объединяемые события несовместны (никакие два из них не могут произойти одновременно), то вероятность объединения нескольких событий равна сумме вероятностей объединяемых событий (аксиома сложения вероятностей):
P(А1∪ А2∪... ∪ Аn) = P(А1) + P(А2) +... + P(Аn)
Событие, состоящее в ненаступлении случайного события А, называется событием, противоположным событию А, и обозначается через  . Объединение событий А и дает событие достоверное, а так как события А и несовместны, то
P(A) + P() = 1, или Р() = 1 - Р(А).
Если в результате данного испытания может наступить лишь одно из несовместных событий А1, А2,..., Аn, то события А1, А2,..., Аn образуют так называемую полную группу событий. Так как объединение событий полной группы является событие достоверным, то для таких событий имеет место равенство
P(А1) + P(А2) +... + P(Аn) = 1
Пересечением (или совмещением, произведением) двух случайных событий А1 и А2называется сложное событие, заключающееся в одновременном или последовательном осуществлении обоих событий. Совмещение событий А1 и А2 обозначается через А1∩А2 или А1А2. Под условной вероятностью события А2 по отношению к событию А1 [обозначается Р(А2/А1)] понимается вероятность осуществления события А2, определенная в предположении, что событие А1имело место. Вероятность совмещения двух событий А1 и А1 равна произведению вероятности одного из них на условную вероятность второго по отношению к первому (аксиома умножения вероятностей):
P(А1∩А2) = P(А1) · Р(А2/А1) = P(А2) · Р(А1/А2).
Два случайных события А1 и А2 называются независимыми, если условная вероятность одного из них по отношению к другому равна безусловной вероятности этого же события: Р(А2/А1) = P(А2). В этом случае имеют место равенства:
P(А2/ 1) = P(А2/A1) = P(А2); P(А1/A2) = P(А1/ 2) = P(А1);
Для независимых событий вероятность их совмещения равна произведению их вероятностей:
P(А1∩А2) = P(А1) · Р(А2)
Совмещение n событий А1, А2,..., Аn (определяемое аналогично) обозначается через А1∩А2∩... ∩Аn. Условная вероятность события Аk, определенная в предположении, что осуществились события А1, А2,..., Аk-1, обозначается P(Аk/А1∩А2∩... ∩Аk-1). Вероятность совмещения n событий по аксиоме умножения вероятностей определяется формулой
P(А1∩А2∩... ∩Аn) = P(А1)·Р(А2/А1)·Р(А3/А1∩А2)·...·P(Аn/А1∩А2∩... ∩Аn-1).
Говорят, что n событий А1, А2,..., Аn называются независимыми в их совокупности, если на вероятность осуществления каждого из них не оказывает влияния осуществление любых других, взятых в какой угодно комбинации. Вероятность совмещения n событий, независимых в их совокупности, равна произведению их вероятностей:
P(А1∩А2∩... ∩Аn) = P(А1)·P(А2)·...·P(Аn). Задача 1 В урне 10 белых, 15 черных, 20 синих и 25 красных шаров. Вынули один шар. Найти вероятность того, что вынутый шар: белый; черный; синий; красный; белый или черный; синий или красный; белый, черный или синий. Решение. Имеем n=10+15+20+25=70, Р(Б)=10/70=1/7, Р(Ч)=15/70=3/14, Р(С)=20/70=2/7, Р(К)=25/70=5/14. Применив аксиому сложения вероятностей, получим
Р(Б+Ч) = Р(Б) + Р(Ч) = 1/7 + 3/14 = 5/14; Р(С+К) = Р(С) + Р(К) = 2/7 + 5/14 = 9/14; Р(Б+Ч+С) = 1 - Р(К) = 1 - 5/4 = 9/14;
Задача 2 В первом ящике 2 белых и 10 черных шаров; во втором ящике 8 белых и 4 черных шара. Из каждого ящика вынули по шару. Какова вероятность, что оба шара белые? Решение. В данном случае речь идет о совмещении событий А и В, где событие А - появление белого шара из первого ящика. При этом А и В - независимые события. Имеем Р(А)=2/12=1/6, Р(В)=8/12=2/3. Применив аксиому умножения вероятностей, находим Р(А∩В) = Р(А)·Р(В)=(1/6)·(2/3)=1/9. Задача 3 Три стрелка стреляют по цели. Вероятность попадания в цель для первого стрелка равна 0,75, для второго - 0,8, для третьего - 0,9. Определить вероятность того, что все три стрелка одновременно попадут в цель и вероятность того, что в цель попадет хотя бы один стрелок. Решение. Имеем Р(A) = 0,75, P(B)=0,8, P(C)=0,9. Тогда вероятность, что все три стрелка попадут в цель Р(А∩В∩С)=P(A)·P(B)·P(C)=0,75·0,8·0,9=0,54. Вероятность промаха первого стрелка: Р()=1-Р(А)=1-0,75=0,25. Вероятность промаха второго и третьего стрелка соответственно 0,2 и 0,1. Тогда вероятность одновременного промаха всех стрелков 0,25·0,2·0,1=0,005. Но событие, противоположное к этому, является событие, заключающееся в поражении цели хотя бы одним стрелком. Следовательно, искомая вероятность равна 1-0,005=0,995.
|
Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени...
|
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Статика является частью теоретической механики, изучающей условия, при которых тело находится под действием заданной системы сил...
|
Теория усилителей. Схема Основная масса современных аналоговых и аналого-цифровых электронных устройств выполняется на специализированных микросхемах...
|
Логические цифровые микросхемы Более сложные элементы цифровой схемотехники (триггеры, мультиплексоры, декодеры и т.д.) не имеют...
|
|
Понятие метода в психологии. Классификация методов психологии и их характеристика Метод – это путь, способ познания, посредством которого познается предмет науки (С...
ЛЕКАРСТВЕННЫЕ ФОРМЫ ДЛЯ ИНЪЕКЦИЙ К лекарственным формам для инъекций относятся водные, спиртовые и масляные растворы, суспензии, эмульсии, новогаленовые препараты, жидкие органопрепараты и жидкие экстракты, а также порошки и таблетки для имплантации...
Тема 5. Организационная структура управления гостиницей 1. Виды организационно – управленческих структур. 2. Организационно – управленческая структура современного ТГК...
|
|
Машины и механизмы для нарезки овощей В зависимости от назначения овощерезательные машины подразделяются на две группы: машины для нарезки сырых и вареных овощей...
Классификация и основные элементы конструкций теплового оборудования Многообразие способов тепловой обработки продуктов предопределяет широкую номенклатуру тепловых аппаратов...
Именные части речи, их общие и отличительные признаки Именные части речи в русском языке — это имя существительное, имя прилагательное, имя числительное, местоимение...
|
|
