Опр. Линейное пространство, в котором существует базис из n векторов назовем n-мерным, а число n-размерностью пространства. Размерность нулевого пространства =0. Любые точки найдется в пространстве n независимых векторов такое что пространство будет называться бесконечно мерным.Множ-во векторов на плоскости является двумерным, а в пространстве трехмерным линейным пространством.Линейное пространство столбцов имеет размерность n. Линейное пространство непрерывных функций одного аргумента t 0 ≤ t ≤ 1является бесконечно мерным.Любые т. существует n линейно независимых векторов х°,х1,...хт-1. Тогда линейная комбинация векторов α0+ α1x+ α2x2+… αmxm - это выражение тождественно равно нулю (должно быть), Линейно зависимая комбинация, но оно не равно нулю.В пространстве конечной размерности существует бесконечно много различных базисов, это видно из предложения 1.
Предложение 1 В n-мерном пространстве каждая упорядоченная система из n является базисом. Док-во: Если дана такая система век-ов, то каждый вектор пространства раскладывается по этим векторам, иначе мы бы пришли к n -1 независимых векторов, а это противоречит размерности пространства. Ч.Т.Д. Предложение 2. В n мерном пространстве каждая упорядоченная линейно независимая система из k<n можно дополнить до базиса.Док-во: Можно присоединить еще один вектор, к-ый через нее не выражается (если бы это было не так, то это базис). Теперь имеем к+1линейно независимый вектор, можно присоединить еще один вектор, к-ый через нее не выражается. Действуем так до к+...=n,следовательно, до базиса мы можем дополнить ненулевой вектор. Ч.Т.Д.
53.Замена базиса. Если в n-мерном пространстве дан базис ( ) и (
) и (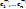 ), то каждый вектор второго мы можем разместить через первый базис:
), то каждый вектор второго мы можем разместить через первый базис: 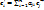 (1)
(1)
, распишем 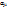 : А=
: А=  Обозначим эту матрицу через А. Столбцы матрицы А координатные столбцы (
Обозначим эту матрицу через А. Столбцы матрицы А координатные столбцы ( ) в базисе (
) в базисе ( ). Поэтому столбцы матрицы А линейно независимы и detА
). Поэтому столбцы матрицы А линейно независимы и detА  0. Опр. Матрицу ij столбец к-ой есть координатный столбец
0. Опр. Матрицу ij столбец к-ой есть координатный столбец  по базису (
по базису ( ) мы назовем матрицей перехода от матрицы e к
) мы назовем матрицей перехода от матрицы e к  или
или  =eА .(2) Умножим обе части этого равенства на
=eА .(2) Умножим обе части этого равенства на 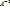 (справа), получим e=
(справа), получим e=  , отсюда следует, что
, отсюда следует, что 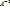 будет матрицей перехода от
будет матрицей перехода от  к базису e. Предложение 6. Задан базис e. Каждая матрица А(detА
к базису e. Предложение 6. Задан базис e. Каждая матрица А(detА  0) служит матрицей перехода e к базису
0) служит матрицей перехода e к базису  . Док-во: Если detА
. Док-во: Если detА  , то столбцы матрицы А линейно независимы, и они служат координатными столбцами n линейно независимых век-ов, к-ые составляют нам нужный базис
, то столбцы матрицы А линейно независимы, и они служат координатными столбцами n линейно независимых век-ов, к-ые составляют нам нужный базис  .Выясним, как связаны между собой координаты базисов e и
.Выясним, как связаны между собой координаты базисов e и  . Рассмотрим вектор x x=
. Рассмотрим вектор x x=  в одном базисе и
в одном базисе и  в другом базисе. Получим: x=
в другом базисе. Получим: x=  x=eА
x=eА  ; e
; e  ;e
;e 
 (3)
(3)
 *
*  Это и есть формула перехода:
Это и есть формула перехода: 
54.Линейное подпространство. Опр. Непустое мн-воZ’ век-ов в линейном пространстве Z называется линейном подпространством, если:A)Сумма любых век-ов из 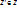 ; Б)Произведение каждого ветора из
; Б)Произведение каждого ветора из  на число также
на число также  . Из определение следует: любая линейная век-ов из
. Из определение следует: любая линейная век-ов из  .
.


 вектор; (-1)
вектор; (-1) 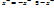 противоположенный. Все 8 аксиом линейного пространства будут выполняться в
противоположенный. Все 8 аксиом линейного пространства будут выполняться в  и следовательно
и следовательно  -также является линейным пространством. Пример 1: Дано некоторое множество P век-ов линейного пространства Z, обозначим через
-также является линейным пространством. Пример 1: Дано некоторое множество P век-ов линейного пространства Z, обозначим через  совокупности всевозможных линейных комбинаций, каждая из которых составлено из целого числа век-ов
совокупности всевозможных линейных комбинаций, каждая из которых составлено из целого числа век-ов  -при Z.
-при Z.  вектор – линейная комбинация k-век-ов: x=
вектор – линейная комбинация k-век-ов: x= 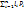 ; y=
; y= 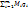 от сюда следует, x+y=
от сюда следует, x+y= 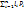 +
+  -снова линейная комбинация из P.Если
-снова линейная комбинация из P.Если  умножим на число, то:
умножим на число, то:  линейная комбинация.Построенное подпространство
линейная комбинация.Построенное подпространство  наз-ся оболочкой множества P.Пусть
наз-ся оболочкой множества P.Пусть 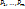 - независимая линейная комбинация век-ов из P, обладающая тем свойством, что каждый вектор из P есть линейная комбинация этих век-ов.Тогда
- независимая линейная комбинация век-ов из P, обладающая тем свойством, что каждый вектор из P есть линейная комбинация этих век-ов.Тогда 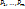 - базис в линейной оболочке множества P. В частности, если P – конечное множество век-ов. Утверждение 1. Размерность линейной оболочки конечного мно-ва век-ов не превосходит числа этих век-ов.
- базис в линейной оболочке множества P. В частности, если P – конечное множество век-ов. Утверждение 1. Размерность линейной оболочки конечного мно-ва век-ов не превосходит числа этих век-ов.
Пример 2: Рассмотр. однородную систему линейных уравнений с n-неизвестными. Совокупность всех решений этой сис-мы представляет собой подпространство линейного пространства столбцов высоты n.Тогда фундаментальная сис-ма решений-базис.В каждом линейном пространстве множества состоящего из одно нулевого вектора, является линейным подпространством оно называется нулевым подпространством.
Пример 3 Множество состоящее из всех век-ов пространства Z, является подпространством Z и оно является всем пространством Z. Утверждение 2 Пусть Z’- подпространство Z –мерного пространства  , тогда размерность
, тогда размерность  =k
=k  n. Если k=n, то
n. Если k=n, то  =
=  .Док-во: Необходимо для случая, когда
.Док-во: Необходимо для случая, когда  -ненулевое подпространство. Мы можем исходя из любого ненулевого подпространства построить базис. Процесс построения должен закончится на не большем n, т.к. каждая линейно незав. комбинация есть такая же система n векторов
-ненулевое подпространство. Мы можем исходя из любого ненулевого подпространства построить базис. Процесс построения должен закончится на не большем n, т.к. каждая линейно незав. комбинация есть такая же система n векторов  и следовательно не может содержать более чем n векторов.Пусть базис в
и следовательно не может содержать более чем n векторов.Пусть базис в  содержит n-век-ов, тогда любой вектор из
содержит n-век-ов, тогда любой вектор из  раскладывается по базису, и таким образом принадлежит
раскладывается по базису, и таким образом принадлежит  . Т.о.
. Т.о.  совпадает с
совпадает с  . Ч.Т.Д.
. Ч.Т.Д. 
 -линейная оболочка своего базиса, то из утв.2 следует что каждое подпространство конечномерного пространства есть линейная оболочка конечного множества век-ов.
-линейная оболочка своего базиса, то из утв.2 следует что каждое подпространство конечномерного пространства есть линейная оболочка конечного множества век-ов.
53.Замена базиса. Если в n-мерном пространстве дан базис ( ) и (
) и (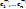 ), то каждый вектор второго мы можем разместить через первый базис:
), то каждый вектор второго мы можем разместить через первый базис: 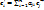 (1)
(1)
, распишем 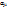 : А=
: А= 
Обозначим эту матрицу через А. Столбцы матрицы А координатные столбцы ( ) в базисе (
) в базисе ( ). Поэтому столбцы матрицы А линейно независимы и detА
). Поэтому столбцы матрицы А линейно независимы и detА  0. Опр. Матрицу ij столбец к-ой есть координатный столбец
0. Опр. Матрицу ij столбец к-ой есть координатный столбец  по базису (
по базису ( ) мы назовем матрицей перехода от матрицы e к
) мы назовем матрицей перехода от матрицы e к  или
или  =eА .(2) Умножим обе части этого равенства на
=eА .(2) Умножим обе части этого равенства на 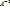 (справа), получим e=
(справа), получим e=  , отсюда следует, что
, отсюда следует, что 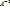 будет матрицей перехода от
будет матрицей перехода от  к базису e. Предложение 6. Задан базис e. Каждая матрица А(detА
к базису e. Предложение 6. Задан базис e. Каждая матрица А(detА  0) служит матрицей перехода e к базису
0) служит матрицей перехода e к базису  . Док-во: Если detА
. Док-во: Если detА  , то столбцы матрицы А линейно независимы, и они служат координатными столбцами n линейно независимых век-ов, к-ые составляют нам нужный базис
, то столбцы матрицы А линейно независимы, и они служат координатными столбцами n линейно независимых век-ов, к-ые составляют нам нужный базис  .Выясним, как связаны между собой координаты базисов e и
.Выясним, как связаны между собой координаты базисов e и  . Рассмотрим вектор x x=
. Рассмотрим вектор x x=  в одном базисе и
в одном базисе и  в другом базисе. Получим:
в другом базисе. Получим:
x= 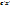 ; x=eА
; x=eА  ; e
; e  ; e
; e 
 (3)
(3)
 *
*  Это и есть формула перехода:
Это и есть формула перехода:
56.Линейное отображение. Пусть Z и  - линейное пространства,оба вещественные или оба комплексные. Под отображением А в простран. Z и
- линейное пространства,оба вещественные или оба комплексные. Под отображением А в простран. Z и  понимается закон, по которому каждому вектору из Z сопоставлен единственный вектор из
понимается закон, по которому каждому вектору из Z сопоставлен единственный вектор из  .(обозначаем образ-вектор x через А(x)). Опр. Отображение А из Z в
.(обозначаем образ-вектор x через А(x)). Опр. Отображение А из Z в  называется линейным, если для любых 2-х векторов y и x
называется линейным, если для любых 2-х векторов y и x  Z и любого числа
Z и любого числа  выполнено: 1) А(x+y)=А(x)+А(y), 2)А(
выполнено: 1) А(x+y)=А(x)+А(y), 2)А( x)=
x)= 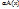 .Линейное отображение мы будем называть линейным преобразованием, если постр. Z и
.Линейное отображение мы будем называть линейным преобразованием, если постр. Z и  совпадают.Из определения следует, что линейная комбинация векторов при линейном отображении переходит в линейную комбинацию их образов.
совпадают.Из определения следует, что линейная комбинация векторов при линейном отображении переходит в линейную комбинацию их образов.
Пример:лин. отобр.1: 
 -фиксированное число. Сопоставим каждому вектору x
-фиксированное число. Сопоставим каждому вектору x  Z вектор
Z вектор  x, можно видеть, что линейное преобразование. Выберем в
x, можно видеть, что линейное преобразование. Выберем в  базис, это сопоставит каждому вектору его координатный столбец и следовательно определит линейное отображение, р/м пространство столбцов высоты n. Если мы сопоставим каждому вектору x 1-ую его компоненту, то получим отображение
базис, это сопоставит каждому вектору его координатный столбец и следовательно определит линейное отображение, р/м пространство столбцов высоты n. Если мы сопоставим каждому вектору x 1-ую его компоненту, то получим отображение  в пространство R.
в пространство R.
В силу правил действия с координатами векторов такое отображение – линейное. Такие отображения линейные функции.
Предложение 1: При линейном отображении А простр.  линейное подпространство
линейное подпространство 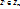 переходит в линейное подпространство А(
переходит в линейное подпространство А( )
) 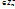 , причем размерность А(
, причем размерность А( )≤размерности
)≤размерности  : dim (А(
: dim (А( )) ≤dim(
)) ≤dim( ).
).
Док-во: Пусть  - базис в
- базис в  . Для любых x
. Для любых x 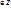 ,
,  , Аx=А(
, Аx=А( ) = А
) = А 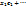 А
А  (2)
(2)
Это означает, что произвольный элемент А( ) есть линейная комбинация А
) есть линейная комбинация А  , и следовательно оно есть подпространством, размерность этого подпростр. Не превосходит k. Ч.Т.Д.
, и следовательно оно есть подпространством, размерность этого подпростр. Не превосходит k. Ч.Т.Д.
57.Координатная запись линейного отображения. Опр. Матрица линейного отображения А  в
в  в паре базисов e и f
в паре базисов e и f  ,
,  называется матрица корд. столбцами векторов А(
называется матрица корд. столбцами векторов А( )…А(
)…А( ).Матрица лин. отображения в след. системе однозначно определена. Если для любого
).Матрица лин. отображения в след. системе однозначно определена. Если для любого  представим как вектор
представим как вектор  на вектор x:
на вектор x:  . Столбцы матрицы В
. Столбцы матрицы В 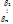 совпадут со столбцами матрицы А и матрица В совпадет с матрицей А. Умножим матр. В на координ. столбец вектора
совпадут со столбцами матрицы А и матрица В совпадет с матрицей А. Умножим матр. В на координ. столбец вектора  (столбец единичной матрицы), очевидно, что произведение =I столбцу матрицы В, а это и есть координатный столбец А
(столбец единичной матрицы), очевидно, что произведение =I столбцу матрицы В, а это и есть координатный столбец А  .Последний пример лин. отображ. Показывает, что каждая матрица размеров m
.Последний пример лин. отображ. Показывает, что каждая матрица размеров m  n служит матрицей некоторого лин. отображ. простр.
n служит матрицей некоторого лин. отображ. простр.  в
в  .Т.о., мы видим, что выбор базиса в простран.
.Т.о., мы видим, что выбор базиса в простран.  и
и  устанавливается взаимооднозначное соответствие между линю отображением и матрицей размерности m
устанавливается взаимооднозначное соответствие между линю отображением и матрицей размерности m  n. Предложение 4 Ранг матрицы лин. отображения = рангу этого отображения. Док-во:
n. Предложение 4 Ранг матрицы лин. отображения = рангу этого отображения. Док-во: 
 , в кот-ом расположен базисный минор матр.А. Это значит, что вектора А(
, в кот-ом расположен базисный минор матр.А. Это значит, что вектора А(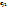 )…А(
)…А( ) линейно независимы и каждый вектор
) линейно независимы и каждый вектор  (i=1…n) есть линейная комбинация этих векторов, следовательно мы можем выразить образ любого вектора через (А
(i=1…n) есть линейная комбинация этих векторов, следовательно мы можем выразить образ любого вектора через (А 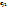 …А
…А  ),
),
т.о., они образуют базис во множестве значений А и их число = размерности промтр. А  т.е. ранг отображения. Ч.Т.Д. Из предложения 4 вытекает:
т.е. ранг отображения. Ч.Т.Д. Из предложения 4 вытекает:  матрицы линейного отображения один и тот же какую бы пару базисов мы не взяли. Предложение 5 Сумма
матрицы линейного отображения один и тот же какую бы пару базисов мы не взяли. Предложение 5 Сумма  отображений и размерности его ядра = размерности отображаемого пространства.Док-во: Согласно предложению ядро отображения определяется однородной системой лин. уравнений. Аx=
отображений и размерности его ядра = размерности отображаемого пространства.Док-во: Согласно предложению ядро отображения определяется однородной системой лин. уравнений. Аx=  (с n неизвестными). Так видно из предл. 4. Ранг матрицы этой с-мы=рангу отображения и равен r.
(с n неизвестными). Так видно из предл. 4. Ранг матрицы этой с-мы=рангу отображения и равен r.  размерность ядра =d из свойства множества решений однородных уравнений вытекает, что d=n-r, отсюда вытекает, что n=d+r. Ч.Т.Д. Частный случай: r=n ядро является нулевым, и отображение является вложением. Взаимоодн. Отобр. Является одновременно и вложением и разложением. Предложение 6 Отображение А:
размерность ядра =d из свойства множества решений однородных уравнений вытекает, что d=n-r, отсюда вытекает, что n=d+r. Ч.Т.Д. Частный случай: r=n ядро является нулевым, и отображение является вложением. Взаимоодн. Отобр. Является одновременно и вложением и разложением. Предложение 6 Отображение А:  в
в  взаимооднозначно тогда и только тогда, когда размерностей пространств совпадают и равны рангу отображения.
взаимооднозначно тогда и только тогда, когда размерностей пространств совпадают и равны рангу отображения.
58.Изоморфизм линейного пространства.Изменение матрицы линейного отображения при замене базиса. Опр. Взаимоодн.лин. отображения лин.пространства назыв. изоморфизмами. 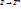 сами пространства – изоморфные.Из предложения 6 следуют, чтобы 2 пространства были изоморфные необходимо и достаточно чтобы их размерности совпадали. Теорема: 2 вещественных пространства изоморфны тогда и только тогда, когда их размерности равны. Тоже верно и для комплексных простанств.Док-во: Достаточность. Пусть Z и
сами пространства – изоморфные.Из предложения 6 следуют, чтобы 2 пространства были изоморфные необходимо и достаточно чтобы их размерности совпадали. Теорема: 2 вещественных пространства изоморфны тогда и только тогда, когда их размерности равны. Тоже верно и для комплексных простанств.Док-во: Достаточность. Пусть Z и  - два изоморф. простр-ва. Если в каждом из них выбран базис, то определяем некот. Отображ.
- два изоморф. простр-ва. Если в каждом из них выбран базис, то определяем некот. Отображ. 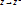 по формуле (5) В = Аx. Это отображение будет изоморфизмом, если ранг матрицы = n. Чтобы задать изоморф.
по формуле (5) В = Аx. Это отображение будет изоморфизмом, если ранг матрицы = n. Чтобы задать изоморф. 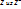 необходимо создать базисы в этих пространствах и задать матрицу ранга r.Изменение матрицы линейного отображения при замене базисов.Рассмотрим лин. отобр А:
необходимо создать базисы в этих пространствах и задать матрицу ранга r.Изменение матрицы линейного отображения при замене базисов.Рассмотрим лин. отобр А:  . В
. В  базис e, в простр.
базис e, в простр.  f. Пусть задана другая с-ма базисов. В
f. Пусть задана другая с-ма базисов. В 
 (
( ), в
), в 
 (
( ). Пусть матрица перехода от базиса e к базису
). Пусть матрица перехода от базиса e к базису  S, а от f к
S, а от f к  P. В базисах
P. В базисах  и
и  отображение А имеет матрицу
отображение А имеет матрицу  . Существует произвольный вектор x из
. Существует произвольный вектор x из  , его образ y=А(x) из
, его образ y=А(x) из  . Обозначим координатные столбцы векора x в базисах
. Обозначим координатные столбцы векора x в базисах 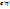 и eη, а координ. cтодбцы y: fз и
и eη, а координ. cтодбцы y: fз и  . Используя формулу перехода к координатам: η=S
. Используя формулу перехода к координатам: η=S  , з=P
, з=P  . Подставим эти выражения в В = Аx, получим: P
. Подставим эти выражения в В = Аx, получим: P  = АS
= АS  . Можно найти
. Можно найти  из этого равенства:
из этого равенства:  =
=  , но с другой стороны
, но с другой стороны  =
= 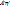 , следовательно
, следовательно 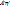 =
=  ,
,  =
=  =
=  АS (6). – матрица лин. отображ. для данной пары базисов. Это и есть связь между матрицами.Если обозначить элемент матр. А -
АS (6). – матрица лин. отображ. для данной пары базисов. Это и есть связь между матрицами.Если обозначить элемент матр. А - 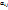 , а элемент матр.
, а элемент матр.  -
- 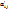 ,
,  -
-  , S-
, S-  , то матричное равенство (6) можем переписать:
, то матричное равенство (6) можем переписать: 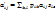 (7),i=1…m, k=1…m,j=1…n,l=1…n.
(7),i=1…m, k=1…m,j=1…n,l=1…n.
59. Канонический вид линейного отображения. Сумма и произведение отображений. Для любого линейного отображения А: α→ά ранг r можно так выбрать базисы: α и ά, что оно будет иметь матрицу  (7) Er – единичная матрица порядка, r остальные элементы, если они есть равны 0. Док-во. Поместим векторы еr+1… еn базиса пространства α в KerA, векторы е1… еr можем выбрать произвольно. В силу такого выбора при любом базисе в ά последние n-r столбцов матрицы А будут нулевыми. Так как RgA=r, первые r столбцов должны быть линейно независимыми. Поэтому линейно независимые векторы А(е1), …, А(еr). Примем их за первые r базисных векторов в пространстве ά, а остальные векторы fr+1, …, fm этого базиса выберем произвольно. При таком выборе первые r столбцов А будут первыми r столбцами единичной матрицы порядка m. Это и есть вид (7).
(7) Er – единичная матрица порядка, r остальные элементы, если они есть равны 0. Док-во. Поместим векторы еr+1… еn базиса пространства α в KerA, векторы е1… еr можем выбрать произвольно. В силу такого выбора при любом базисе в ά последние n-r столбцов матрицы А будут нулевыми. Так как RgA=r, первые r столбцов должны быть линейно независимыми. Поэтому линейно независимые векторы А(е1), …, А(еr). Примем их за первые r базисных векторов в пространстве ά, а остальные векторы fr+1, …, fm этого базиса выберем произвольно. При таком выборе первые r столбцов А будут первыми r столбцами единичной матрицы порядка m. Это и есть вид (7).
Рассмотрим 2 линейных отображения А: α→ά и В: α→ά. Мы назовем суммой этих отображений и обозначим А+В отображение С: α→ά, определяемое равенством С(х)=А(х)+В(х) для любого хϵα. Сумма А+В линейных отображений – линейное отображение, и его матрица равна сумме матриц А+В. Произведение линейного отображения А на число α определяется как отображение В, сопоставляющее вектору х вектор αА(х). Легко проверить, что это отображение линейное и имеет матрицу αА, если А- матрица отображения А. Теперь рассмотрим три линейных пространства α,α’,α’’. Результат последовательного выполнения отображений А и В называется их произведением и обозначается ВА. Пусть в пространствах α,α’,α’’ выбраны базисы соответственно e, f, g. Обозначим через А матрицу отображения А в базисах е и f, а через В – матрицу отображения В в базисах f и g. Отображение ВА имеет матрицу ВА в базисах е и g. Док-во. Рассмотрим координатный столбец ξ произвольного вектора из α. Координатные столбцы векторов А(х) и В(А(х)) обозначим соответственно через η и ζ. Тогда η=Аξ и ζ=Вη=ВАξ. Ранг произведения отображений не превосходит рангов этих отображений. Линейное отображение А имеет обратное тогда и только тогда, когда оно – изоморфизм.
60. Линейные преобразования. Инвариантность подпространств. Линейное преобразование – отображение, которое отображает линейное пространство в то же самое пространство. Матрицей линейного преобразования А: α→ά в базисе е=||е1 … еn|| называется матрица, столбцы которой – координатные столбцы векторов А(е1) … А(еn) в базисе е. Формула для матрицы преобразования А’=S-1AS. Подпространство άСα называется инвариантным относительно А, если для каждого вектора х из ά образ А(х) лежит в ά. Матрица линейного преобразования клеточно-треугольная тогда, когда линейная оболочка базисных векторов е1 … ек – инвариантное подпространство. Матрица линейного преобразования является клеточно – диагональной тогда, когда базис есть объединение базисов инвариантных подпространств. Если преобразование А и В перестановочны, то ядро и множество значений одного из них инвариантны относительно другого. Док-во 1. Если хϵKerА, то А(х)=0, и потому В(А(х))=0. Тогда А(В(х))=0, а значит В(х)ϵKerА. 2. Если хϵ ImA, то существует вектор я такой, что х=А(z). Тогда В(х)=В(А(z))=А(В(z)). Это означает, что В(х)ϵ ImА.
61. Собственные векторы. Собственные числа. Теорема 1 Собственными числами матрицы 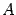 являются корни уравнения
являются корни уравнения 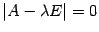 и только они. Определение 1. Матрица
и только они. Определение 1. Матрица  называется характеристической матрицей матрицы
называется характеристической матрицей матрицы 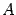 , многочлен
, многочлен 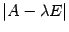 называется характеристическим многочленом матрицы
называется характеристическим многочленом матрицы 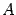 , уравнение
, уравнение 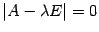 называется характеристическим уравнением матрицы
называется характеристическим уравнением матрицы 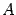 . Определение 2. Ненулевой вектор
. Определение 2. Ненулевой вектор 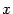 называется собственным вектором линейного преобразования
называется собственным вектором линейного преобразования 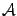 , соответствующим собственному числу l, если
, соответствующим собственному числу l, если 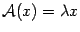 . Определение 3. Совокупность всех собственных чисел линейного преобразования
. Определение 3. Совокупность всех собственных чисел линейного преобразования 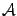 конечномерного линейного пространства называется спектром преобразования
конечномерного линейного пространства называется спектром преобразования 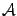 . Вместо слов "собственное число" говорят также собственное значение, характеристическое число или характеристическое значение. Если
. Вместо слов "собственное число" говорят также собственное значение, характеристическое число или характеристическое значение. Если  - двумерное или трехмерное линейное пространство, то собственный вектор линейного преобразования - это такой вектор, образ которого коллинеарен его прообразу[1]. Иными словами, после применения преобразования (в вещественном случае) может измениться длина вектора, а направление или сохранится, или изменится на противоположное, или вектор станет равным нулю (в случае l=0). Утверждение 1. Пусть x- собственный вектор линейного преобразования
- двумерное или трехмерное линейное пространство, то собственный вектор линейного преобразования - это такой вектор, образ которого коллинеарен его прообразу[1]. Иными словами, после применения преобразования (в вещественном случае) может измениться длина вектора, а направление или сохранится, или изменится на противоположное, или вектор станет равным нулю (в случае l=0). Утверждение 1. Пусть x- собственный вектор линейного преобразования 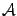 , соответствующий собственному числу l и пусть α - ненулевое число. Тогда αx - тоже собственный вектор линейного преобразования
, соответствующий собственному числу l и пусть α - ненулевое число. Тогда αx - тоже собственный вектор линейного преобразования 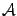 , соответствующий собственному числу l. Определение 3. Ненулевая матрица-столбец α называется собственным вектором квадратной матрицы
, соответствующий собственному числу l. Определение 3. Ненулевая матрица-столбец α называется собственным вектором квадратной матрицы 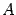 , соответствующим собственному числу l, если выполнено равенство
, соответствующим собственному числу l, если выполнено равенство  . Замечание 1. Между собственными числами (собственными векторами) матрицы и линейного преобразования есть некоторое различие. Линейное преобразование вещественного линейного пространства может не иметь собственных векторов и, соответственно, собственных чисел. Матрица же, как увидим дальше, всегда имеет хотя бы одно собственное число, быть может, комплексное, и ему соответствует собственный вектор (тоже, быть может, комплексный). Но если рассматривать линейные преобразования n-мерных комплексных пространств, то собственные числа преобразований совпадают с собственными числами матриц и собственные векторы преобразований имеют координатными столбцами собственные векторы матриц.
. Замечание 1. Между собственными числами (собственными векторами) матрицы и линейного преобразования есть некоторое различие. Линейное преобразование вещественного линейного пространства может не иметь собственных векторов и, соответственно, собственных чисел. Матрица же, как увидим дальше, всегда имеет хотя бы одно собственное число, быть может, комплексное, и ему соответствует собственный вектор (тоже, быть может, комплексный). Но если рассматривать линейные преобразования n-мерных комплексных пространств, то собственные числа преобразований совпадают с собственными числами матриц и собственные векторы преобразований имеют координатными столбцами собственные векторы матриц.

 ) и (
) и (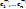 ), то каждый вектор второго мы можем разместить через первый базис:
), то каждый вектор второго мы можем разместить через первый базис: 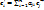 (1)
(1)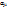 : А=
: А=  Обозначим эту матрицу через А. Столбцы матрицы А координатные столбцы (
Обозначим эту матрицу через А. Столбцы матрицы А координатные столбцы ( ) в базисе (
) в базисе ( ). Поэтому столбцы матрицы А линейно независимы и detА
). Поэтому столбцы матрицы А линейно независимы и detА  0. Опр. Матрицу ij столбец к-ой есть координатный столбец
0. Опр. Матрицу ij столбец к-ой есть координатный столбец  по базису (
по базису ( или
или 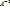 (справа), получим e=
(справа), получим e=  , отсюда следует, что
, отсюда следует, что  к базису e. Предложение 6. Задан базис e. Каждая матрица А(detА
к базису e. Предложение 6. Задан базис e. Каждая матрица А(detА  , то столбцы матрицы А линейно независимы, и они служат координатными столбцами n линейно независимых век-ов, к-ые составляют нам нужный базис
, то столбцы матрицы А линейно независимы, и они служат координатными столбцами n линейно независимых век-ов, к-ые составляют нам нужный базис  в одном базисе и
в одном базисе и  в другом базисе. Получим: x=
в другом базисе. Получим: x=  x=eА
x=eА  ; e
; e  ;e
;e 
 (3)
(3) *
*  Это и есть формула перехода:
Это и есть формула перехода: 
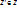 ; Б)Произведение каждого ветора из
; Б)Произведение каждого ветора из  на число также
на число также  . Из определение следует: любая линейная век-ов из
. Из определение следует: любая линейная век-ов из  .
.

 вектор; (-1)
вектор; (-1) 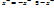 противоположенный. Все 8 аксиом линейного пространства будут выполняться в
противоположенный. Все 8 аксиом линейного пространства будут выполняться в  и следовательно
и следовательно 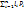 ; y=
; y= 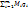 от сюда следует, x+y=
от сюда следует, x+y=  -снова линейная комбинация из P.Если
-снова линейная комбинация из P.Если  умножим на число, то:
умножим на число, то:  линейная комбинация.Построенное подпространство
линейная комбинация.Построенное подпространство 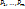 - независимая линейная комбинация век-ов из P, обладающая тем свойством, что каждый вектор из P есть линейная комбинация этих век-ов.Тогда
- независимая линейная комбинация век-ов из P, обладающая тем свойством, что каждый вектор из P есть линейная комбинация этих век-ов.Тогда  , тогда размерность
, тогда размерность  n. Если k=n, то
n. Если k=n, то  совпадает с
совпадает с 
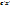 ; x=eА
; x=eА  - линейное пространства,оба вещественные или оба комплексные. Под отображением А в простран. Z и
- линейное пространства,оба вещественные или оба комплексные. Под отображением А в простран. Z и  Z и любого числа
Z и любого числа  выполнено: 1) А(x+y)=А(x)+А(y), 2)А(
выполнено: 1) А(x+y)=А(x)+А(y), 2)А(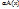 .Линейное отображение мы будем называть линейным преобразованием, если постр. Z и
.Линейное отображение мы будем называть линейным преобразованием, если постр. Z и 
 -фиксированное число. Сопоставим каждому вектору x
-фиксированное число. Сопоставим каждому вектору x  линейное подпространство
линейное подпространство 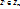 переходит в линейное подпространство А(
переходит в линейное подпространство А(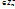 , причем размерность А(
, причем размерность А( - базис в
- базис в 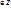 ,
,  , Аx=А(
, Аx=А(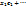 А
А  (2)
(2) , и следовательно оно есть подпространством, размерность этого подпростр. Не превосходит k. Ч.Т.Д.
, и следовательно оно есть подпространством, размерность этого подпростр. Не превосходит k. Ч.Т.Д. в паре базисов e и f
в паре базисов e и f  ,
,  называется матрица корд. столбцами векторов А(
называется матрица корд. столбцами векторов А( )…А(
)…А( ).Матрица лин. отображения в след. системе однозначно определена. Если для любого
).Матрица лин. отображения в след. системе однозначно определена. Если для любого  представим как вектор
представим как вектор  на вектор x:
на вектор x:  . Столбцы матрицы В
. Столбцы матрицы В 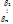 совпадут со столбцами матрицы А и матрица В совпадет с матрицей А. Умножим матр. В на координ. столбец вектора
совпадут со столбцами матрицы А и матрица В совпадет с матрицей А. Умножим матр. В на координ. столбец вектора  (столбец единичной матрицы), очевидно, что произведение =I столбцу матрицы В, а это и есть координатный столбец А
(столбец единичной матрицы), очевидно, что произведение =I столбцу матрицы В, а это и есть координатный столбец А  n служит матрицей некоторого лин. отображ. простр.
n служит матрицей некоторого лин. отображ. простр.  в
в  .Т.о., мы видим, что выбор базиса в простран.
.Т.о., мы видим, что выбор базиса в простран.  , в кот-ом расположен базисный минор матр.А. Это значит, что вектора А(
, в кот-ом расположен базисный минор матр.А. Это значит, что вектора А(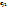 )…А(
)…А( ) линейно независимы и каждый вектор
) линейно независимы и каждый вектор  (i=1…n) есть линейная комбинация этих векторов, следовательно мы можем выразить образ любого вектора через (А
(i=1…n) есть линейная комбинация этих векторов, следовательно мы можем выразить образ любого вектора через (А  матрицы линейного отображения один и тот же какую бы пару базисов мы не взяли. Предложение 5 Сумма
матрицы линейного отображения один и тот же какую бы пару базисов мы не взяли. Предложение 5 Сумма 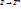 сами пространства – изоморфные.Из предложения 6 следуют, чтобы 2 пространства были изоморфные необходимо и достаточно чтобы их размерности совпадали. Теорема: 2 вещественных пространства изоморфны тогда и только тогда, когда их размерности равны. Тоже верно и для комплексных простанств.Док-во: Достаточность. Пусть Z и
сами пространства – изоморфные.Из предложения 6 следуют, чтобы 2 пространства были изоморфные необходимо и достаточно чтобы их размерности совпадали. Теорема: 2 вещественных пространства изоморфны тогда и только тогда, когда их размерности равны. Тоже верно и для комплексных простанств.Док-во: Достаточность. Пусть Z и 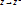 по формуле (5) В = Аx. Это отображение будет изоморфизмом, если ранг матрицы = n. Чтобы задать изоморф.
по формуле (5) В = Аx. Это отображение будет изоморфизмом, если ранг матрицы = n. Чтобы задать изоморф. 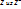 необходимо создать базисы в этих пространствах и задать матрицу ранга r.Изменение матрицы линейного отображения при замене базисов.Рассмотрим лин. отобр А:
необходимо создать базисы в этих пространствах и задать матрицу ранга r.Изменение матрицы линейного отображения при замене базисов.Рассмотрим лин. отобр А:  . В
. В  ), в
), в  (
( ). Пусть матрица перехода от базиса e к базису
). Пусть матрица перехода от базиса e к базису  . Существует произвольный вектор x из
. Существует произвольный вектор x из 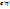 и eη, а координ. cтодбцы y: fз и
и eη, а координ. cтодбцы y: fз и  . Используя формулу перехода к координатам: η=S
. Используя формулу перехода к координатам: η=S  , з=P
, з=P  . Подставим эти выражения в В = Аx, получим: P
. Подставим эти выражения в В = Аx, получим: P  , но с другой стороны
, но с другой стороны 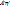 , следовательно
, следовательно  =
=  АS (6). – матрица лин. отображ. для данной пары базисов. Это и есть связь между матрицами.Если обозначить элемент матр. А -
АS (6). – матрица лин. отображ. для данной пары базисов. Это и есть связь между матрицами.Если обозначить элемент матр. А - 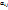 , а элемент матр.
, а элемент матр. 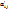 ,
,  , S-
, S-  , то матричное равенство (6) можем переписать:
, то матричное равенство (6) можем переписать: 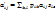 (7),i=1…m, k=1…m,j=1…n,l=1…n.
(7),i=1…m, k=1…m,j=1…n,l=1…n. (7) Er – единичная матрица порядка, r остальные элементы, если они есть равны 0. Док-во. Поместим векторы еr+1… еn базиса пространства α в KerA, векторы е1… еr можем выбрать произвольно. В силу такого выбора при любом базисе в ά последние n-r столбцов матрицы А будут нулевыми. Так как RgA=r, первые r столбцов должны быть линейно независимыми. Поэтому линейно независимые векторы А(е1), …, А(еr). Примем их за первые r базисных векторов в пространстве ά, а остальные векторы fr+1, …, fm этого базиса выберем произвольно. При таком выборе первые r столбцов А будут первыми r столбцами единичной матрицы порядка m. Это и есть вид (7).
(7) Er – единичная матрица порядка, r остальные элементы, если они есть равны 0. Док-во. Поместим векторы еr+1… еn базиса пространства α в KerA, векторы е1… еr можем выбрать произвольно. В силу такого выбора при любом базисе в ά последние n-r столбцов матрицы А будут нулевыми. Так как RgA=r, первые r столбцов должны быть линейно независимыми. Поэтому линейно независимые векторы А(е1), …, А(еr). Примем их за первые r базисных векторов в пространстве ά, а остальные векторы fr+1, …, fm этого базиса выберем произвольно. При таком выборе первые r столбцов А будут первыми r столбцами единичной матрицы порядка m. Это и есть вид (7).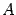 являются корни уравнения
являются корни уравнения 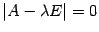 и только они. Определение 1. Матрица
и только они. Определение 1. Матрица  называется характеристической матрицей матрицы
называется характеристической матрицей матрицы 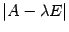 называется характеристическим многочленом матрицы
называется характеристическим многочленом матрицы 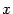 называется собственным вектором линейного преобразования
называется собственным вектором линейного преобразования 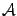 , соответствующим собственному числу l, если
, соответствующим собственному числу l, если 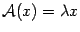 . Определение 3. Совокупность всех собственных чисел линейного преобразования
. Определение 3. Совокупность всех собственных чисел линейного преобразования  - двумерное или трехмерное линейное пространство, то собственный вектор линейного преобразования - это такой вектор, образ которого коллинеарен его прообразу[1]. Иными словами, после применения преобразования (в вещественном случае) может измениться длина вектора, а направление или сохранится, или изменится на противоположное, или вектор станет равным нулю (в случае l=0). Утверждение 1. Пусть x- собственный вектор линейного преобразования
- двумерное или трехмерное линейное пространство, то собственный вектор линейного преобразования - это такой вектор, образ которого коллинеарен его прообразу[1]. Иными словами, после применения преобразования (в вещественном случае) может измениться длина вектора, а направление или сохранится, или изменится на противоположное, или вектор станет равным нулю (в случае l=0). Утверждение 1. Пусть x- собственный вектор линейного преобразования  . Замечание 1. Между собственными числами (собственными векторами) матрицы и линейного преобразования есть некоторое различие. Линейное преобразование вещественного линейного пространства может не иметь собственных векторов и, соответственно, собственных чисел. Матрица же, как увидим дальше, всегда имеет хотя бы одно собственное число, быть может, комплексное, и ему соответствует собственный вектор (тоже, быть может, комплексный). Но если рассматривать линейные преобразования n-мерных комплексных пространств, то собственные числа преобразований совпадают с собственными числами матриц и собственные векторы преобразований имеют координатными столбцами собственные векторы матриц.
. Замечание 1. Между собственными числами (собственными векторами) матрицы и линейного преобразования есть некоторое различие. Линейное преобразование вещественного линейного пространства может не иметь собственных векторов и, соответственно, собственных чисел. Матрица же, как увидим дальше, всегда имеет хотя бы одно собственное число, быть может, комплексное, и ему соответствует собственный вектор (тоже, быть может, комплексный). Но если рассматривать линейные преобразования n-мерных комплексных пространств, то собственные числа преобразований совпадают с собственными числами матриц и собственные векторы преобразований имеют координатными столбцами собственные векторы матриц.


