Мы выяснили, что каждое линейное преобразование n-мерного линейного пространства в фиксированном базисе задается матрицей. Если меняется базис, то, как правило, меняется и матрица. Возникает вопрос, нельзя ли найти базис, в котором матрица линейного преобразования имеет наиболее простой вид. В общем случае выбрать такой базис довольно сложно, что обусловлено поиском нормальной жордановой формы матрицы, изложение которого можно найти в более обстоятельных учебниках по линейной алгебре. Следующая теорема отвечает на этот вопрос в более простом случае. Теорема 2 Пусть 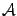 -- линейное преобразование
-- линейное преобразование 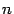 -мерного линейного пространства. Матрица линейного преобразования имеет диагональный вид
-мерного линейного пространства. Матрица линейного преобразования имеет диагональный вид
 тогда и только тогда, когда векторы базиса являются собственнными векторами преобразования
тогда и только тогда, когда векторы базиса являются собственнными векторами преобразования 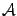 , соответствующими собственным числам
, соответствующими собственным числам 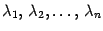 . Следствие Если у матрицы A порядка n существует набор из n линейно независимых собственных векторов, соответствующих собственным числам
. Следствие Если у матрицы A порядка n существует набор из n линейно независимых собственных векторов, соответствующих собственным числам  , то матрица A подобна диагональной матрице с числами
, то матрица A подобна диагональной матрице с числами  на диагонали. Теорема 3. Пусть собственные векторы
на диагонали. Теорема 3. Пусть собственные векторы  преобразования
преобразования 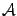 соответствуют собственным числам
соответствуют собственным числам  , среди которых нет равных друг другу. Тогда система векторов
, среди которых нет равных друг другу. Тогда система векторов  является линейно независимой. Следствие Если матрица A порядка n имеет n попарно различных собственных чисел, то она подобна диагональной матрице.
является линейно независимой. Следствие Если матрица A порядка n имеет n попарно различных собственных чисел, то она подобна диагональной матрице.
62. Скалярное произведение. Длина и угол. Определение. назовем длинно вектора x и обозначим |x| число 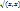 . Углом между векторами x и y назовем каждое число
. Углом между векторами x и y назовем каждое число  , удовлетворяющее условию
, удовлетворяющее условию  В силу аксиомы длина вектора- вещественное неотрицательное число, причем она равна нулю тогда и только тогда, когда вектор нулевой.
В силу аксиомы длина вектора- вещественное неотрицательное число, причем она равна нулю тогда и только тогда, когда вектор нулевой. 
-неравенство, связываемое с именами Шварца, Коши и Буняковского.
Неравенство треугольника  следует из неравенства Коши-Буняковского:
следует из неравенства Коши-Буняковского: 
Знак неравенства имеет место, если 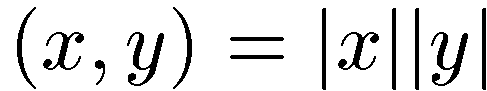 , т.е. если угол между x и y равен нулю, и только в этом случае. Неравенство
, т.е. если угол между x и y равен нулю, и только в этом случае. Неравенство  для векторов – направленных отрезков – означает, что длина стороны треугольника меньше суммы длин остальных его сторон.Векторы x и y называются перпендикулярными или ортогональными, если (x,y)=0. Это условие выполнено, если хоть один из векторов нулевой. Если оба вектора ненулевые, то по
для векторов – направленных отрезков – означает, что длина стороны треугольника меньше суммы длин остальных его сторон.Векторы x и y называются перпендикулярными или ортогональными, если (x,y)=0. Это условие выполнено, если хоть один из векторов нулевой. Если оба вектора ненулевые, то по  угол между ними равен
угол между ними равен 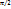 .Только нулевой вектор ортогонален каждому вектору пространства.Действительно, если (x,y)=0 для всех y, то, положив y=x, получим (x,x)=0что возможно только при x=0
.Только нулевой вектор ортогонален каждому вектору пространства.Действительно, если (x,y)=0 для всех y, то, положив y=x, получим (x,x)=0что возможно только при x=0
Скалярное произведение. вещественное линейное пространство  называется евклидовым, если в нем определена операция скалярного умножения: любым двум векторам x и y из
называется евклидовым, если в нем определена операция скалярного умножения: любым двум векторам x и y из  сопоставлено вещественное число(обозначаемое (x,y)), и это соответствие удовлетворяет сл.требованиям, каковы бы ни были вектора x,y и z и число
сопоставлено вещественное число(обозначаемое (x,y)), и это соответствие удовлетворяет сл.требованиям, каковы бы ни были вектора x,y и z и число  :
:
Будем рассматривать n-мерное пространство евклидово пространство  . Любое подпространство
. Любое подпространство  - также евклидово пространство, т.к. для его векторов определено то же самое скалярное умножение. Т.к. (x,
- также евклидово пространство, т.к. для его векторов определено то же самое скалярное умножение. Т.к. (x,  =
=  , имеем (x,
, имеем (x,  =
=  Аналогично доказывается
Аналогично доказывается  можно дасть второе определение евклидова пространства, эквивалентное первому. Вещественное линейное пространство называется евклидовым, если в нем задана положительная определенная квадратичная форма. Из первого определения следует второе. Действительно,если в вещественном линейном пространстве определена операция скалярного умножения, то это- функция от двух векторов. Аксиомы 2),3) и формулы(x,
можно дасть второе определение евклидова пространства, эквивалентное первому. Вещественное линейное пространство называется евклидовым, если в нем задана положительная определенная квадратичная форма. Из первого определения следует второе. Действительно,если в вещественном линейном пространстве определена операция скалярного умножения, то это- функция от двух векторов. Аксиомы 2),3) и формулы(x,  =
= 
 равносильны тому,что функция билинейная. Аксиома 1) означает, что билинейная функция симметрична, а аксиома 4)-что соответствующая квадратичная форма положительно определена. Поскольку симметричная билинейная функция однозначно определяется соответствующей квадратичной формой, обратное утверждение столь же очевидно.В вещественном линейном пространстве существует бесконечно много положительно определенных квадратичных форм. Во втором определении слово «задана» означает, что одна из них выделена и играет особую роль. Будем называть ее основной квадратичной формой.
равносильны тому,что функция билинейная. Аксиома 1) означает, что билинейная функция симметрична, а аксиома 4)-что соответствующая квадратичная форма положительно определена. Поскольку симметричная билинейная функция однозначно определяется соответствующей квадратичной формой, обратное утверждение столь же очевидно.В вещественном линейном пространстве существует бесконечно много положительно определенных квадратичных форм. Во втором определении слово «задана» означает, что одна из них выделена и играет особую роль. Будем называть ее основной квадратичной формой.
Для векторов геометрического пространства скалярное произведение двух векторов определено как произведение их длин на косинус угла между ними. Так, определенная операция скалярного умножения обладает нужными свойствами, но зависит от выбора единицы измерения длин. Поэтому, если такая единица выбрана, векторы геометрического пространства образуют трехмерное евклидово пространство в определенном здесь смысле.В n-мерном арифметическом пространстве мы можем ввести скалярное умножение, сопоставив столбцами  и
и  число
число  через
через  обозначены элементы столбцов.В пространстве функций, непрерывных на отрезке [0,1], можно ввести скалярное произведение по формуле
обозначены элементы столбцов.В пространстве функций, непрерывных на отрезке [0,1], можно ввести скалярное произведение по формуле  аксиомы вытекают из известных свойств определенных интегралов.
аксиомы вытекают из известных свойств определенных интегралов.
63. Ортонормированный базис. Базис, в котором основная квадратичная форма имеет канонический вид, называется ортонормированным базисом. Т.к. она положительно определена, матрица Грамма ортонормированного базиса единичная: 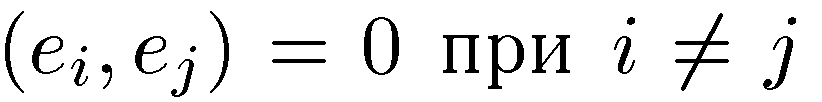
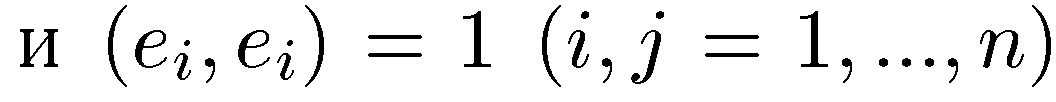 . Это значит, что векторы ортонормированного базиса попарно ортогональны, а по длине равны единице. Для ортонормированного базиса формула
. Это значит, что векторы ортонормированного базиса попарно ортогональны, а по длине равны единице. Для ортонормированного базиса формула  имеет вид:
имеет вид: 
n попарно ортогональных ненулевых векторов  в n-мерном евклидовом пространстве составляют базис. Разложение вектора по этому базису задается формулой
в n-мерном евклидовом пространстве составляют базис. Разложение вектора по этому базису задается формулой  действительно, матрица из произведений
действительно, матрица из произведений 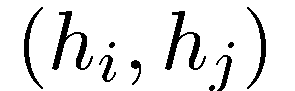 диагональная с ненулевыми элементами на диагонали. Из теоремы следует, что
диагональная с ненулевыми элементами на диагонали. Из теоремы следует, что  , составляют базис.
, составляют базис.
Пусть  . Умножая это равенство скалярно на любой из
. Умножая это равенство скалярно на любой из  , находим, что
, находим, что 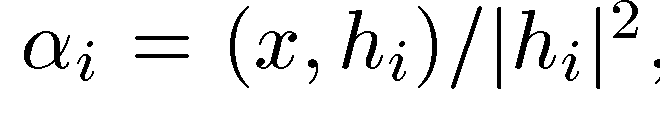 , что равносильно. Базис из ортогональных векторов называется ортогональным базисом. Вычислим (x,x) с помощью формулы
, что равносильно. Базис из ортогональных векторов называется ортогональным базисом. Вычислим (x,x) с помощью формулы  . Поскольку
. Поскольку 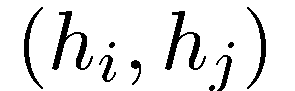 =0 при
=0 при  , получаем равенство Парсеваля
, получаем равенство Парсеваля 
Выражение скалярного произведения через координаты сомножителей. Если в евклидовом пространстве выбран базис e, то скалярное произведение векторов x и y, как и значение любой билинейной функции, выражается по формуле 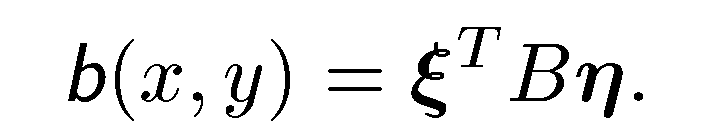 через координатные столбцы
через координатные столбцы 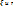 этих векторов:
этих векторов: 
Согласно определению матрицы билинейной функции элементы 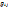 матрицы Г равны скалярным произведениям
матрицы Г равны скалярным произведениям  ,т.е.
,т.е. 
Эта матрица называется матрицей Грама базиса e.Матрица Грама симметрична. По критерию Сильвестра все ее главные миноры положительны, в частности справедливо
Предложение2.Детерминант матрицы Грама любого базиса положителен. Это предложение может быть обобщено сл.образом. Теорема1. Пусть  -произвольная, не обязательно линейно независимая система векторов. Тогда детерминант матрицы, составленной из них попарных скалярных произведений,
-произвольная, не обязательно линейно независимая система векторов. Тогда детерминант матрицы, составленной из них попарных скалярных произведений, 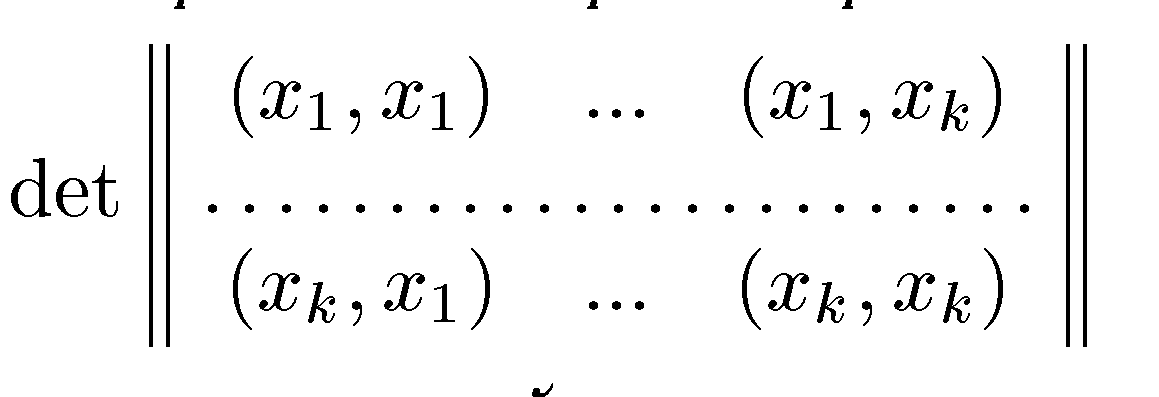 положителен, если векторы линейно независимы, и равен нулю, если они линейно зависимы. Первое утверждение следует из предложения2,т.к. линейно независимые векторы составляют базис в своей линейной оболочке. Докажем второе утверждение. Если вектора линейно зависимые, то выполнено равенство
положителен, если векторы линейно независимы, и равен нулю, если они линейно зависимы. Первое утверждение следует из предложения2,т.к. линейно независимые векторы составляют базис в своей линейной оболочке. Докажем второе утверждение. Если вектора линейно зависимые, то выполнено равенство 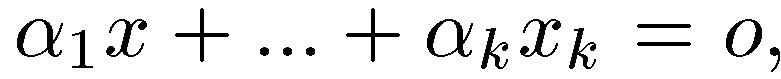 , в котором среди коэффициентов есть отличные от нуля. Умножая это равенство скалярно на каждый из векторов, мы придем к системе линейных уравнений
, в котором среди коэффициентов есть отличные от нуля. Умножая это равенство скалярно на каждый из векторов, мы придем к системе линейных уравнений
 которой удовлетворяют коэффициент
которой удовлетворяют коэффициент 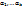 . Т.к. система имеет нетривиальное решение, детерминант ее матрицы равен нулю.
. Т.к. система имеет нетривиальное решение, детерминант ее матрицы равен нулю.
Следствие. Для любых двух векторов в евклидовом пространстве имеет место неравенство Коши-Буняковского, причем оно выполнено как равенство тогда и только тогда, когда вектора линейной зависимы. Пусть базис  связан с базисом e матрицей перехода S. Тогда формула
связан с базисом e матрицей перехода S. Тогда формула  переписывается в виде
переписывается в виде 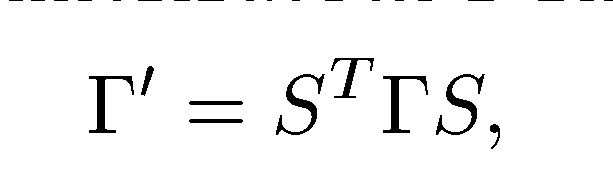 , показывающая связь матрицы Грама двух разных базисов
, показывающая связь матрицы Грама двух разных базисов
65.Ортогональные матрицы. Рассмотрим два ортогональных базиса  и
и  . Тогда в формуле (
. Тогда в формуле ( )
)  , и формула принимает вид
, и формула принимает вид 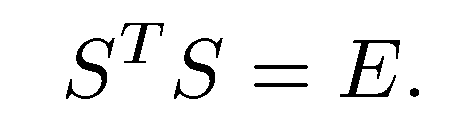
Наоборот, если выполнено условие 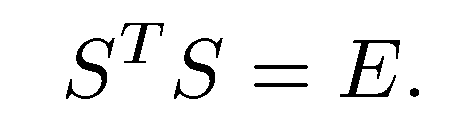 и исходный базис ортонормированный, то мы получаем
и исходный базис ортонормированный, то мы получаем 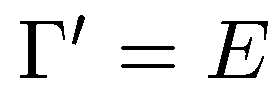 , и новый базис также ортонормированный.
, и новый базис также ортонормированный.
Матрица, удовлетворяющая условию 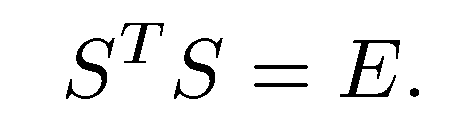 , называется ортогональной матрицей.
, называется ортогональной матрицей.
Ортогональные матрицы и только они могут служить матрицам перехода от одно 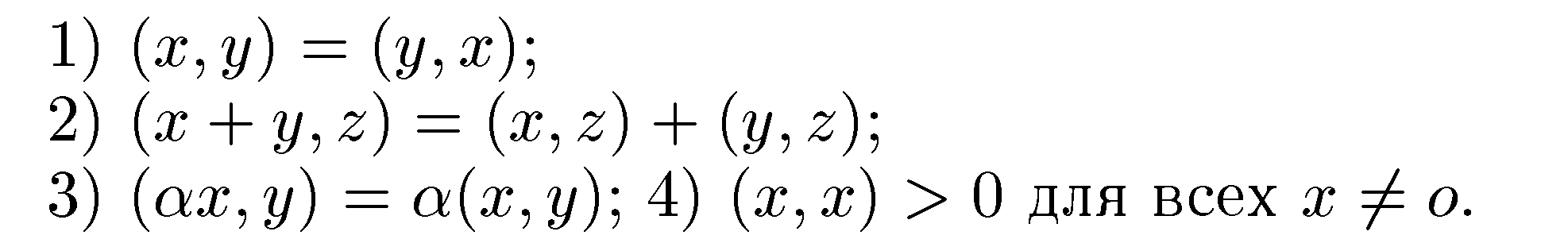 го ортонормированного базиса к другому. Равенство
го ортонормированного базиса к другому. Равенство 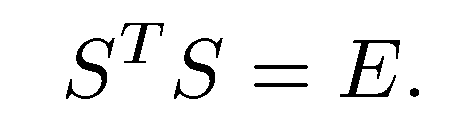 равносильно равенству
равносильно равенству  из свойств обратной матрицы теперь следует, что
из свойств обратной матрицы теперь следует, что 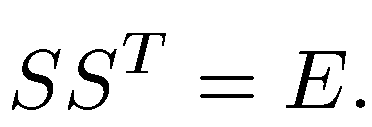 это означает, что матрица
это означает, что матрица 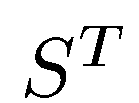 также является ортогональной. Обозначив элементы матрицы S через
также является ортогональной. Обозначив элементы матрицы S через  , мы может написать равенства, равносильные
, мы может написать равенства, равносильные 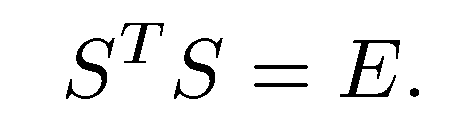 и
и 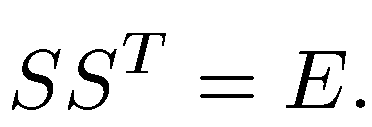 :
:
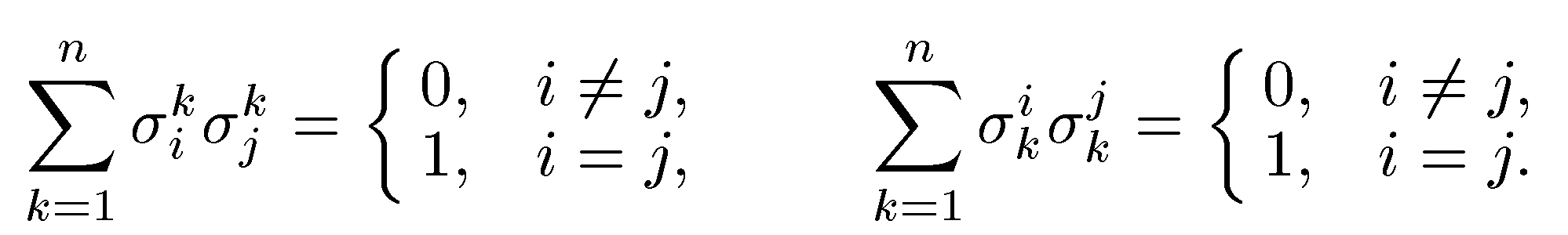 первое из неравенств можно получить непосредственно из
первое из неравенств можно получить непосредственно из  , если вспомнить, что столбцы матрицы перехода - координатные столбцы новых базисных векторов в старом базисе.Произведение SUдвух ортогональных матриц S и U-ортогональная матрица. Действительно,
, если вспомнить, что столбцы матрицы перехода - координатные столбцы новых базисных векторов в старом базисе.Произведение SUдвух ортогональных матриц S и U-ортогональная матрица. Действительно,  . Вычисляя детерминант обеих частей равенства
. Вычисляя детерминант обеих частей равенства 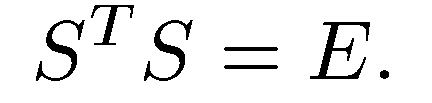 , мы получим
, мы получим 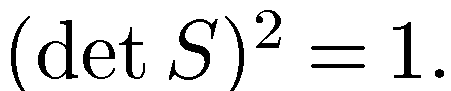 Значит, для ортогональной матрицы
Значит, для ортогональной матрицы 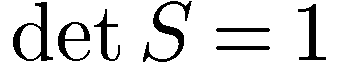 или -1.Любая ортогональная матрица порядка 2 имеет один из двух видов:
или -1.Любая ортогональная матрица порядка 2 имеет один из двух видов:

Ортогональное дополнение подпространства. Пусть  - k-мерное подпространство в n-мерном евклидовом пространстве
- k-мерное подпространство в n-мерном евклидовом пространстве  .Ортогональным дополнением подпространства
.Ортогональным дополнением подпространства  называется множество всех векторов, ортогональных каждому вектору из
называется множество всех векторов, ортогональных каждому вектору из  . Это множество обозначается
. Это множество обозначается  .Ортогональное дополнение k-мерного подпространства в n-мерном пространстве есть (n-k)-мерное подпространство.Док-во. Пусть
.Ортогональное дополнение k-мерного подпространства в n-мерном пространстве есть (n-k)-мерное подпространство.Док-во. Пусть  - базис в
- базис в  . Вектор x лежит в
. Вектор x лежит в  тогда и только тогда, когда
тогда и только тогда, когда 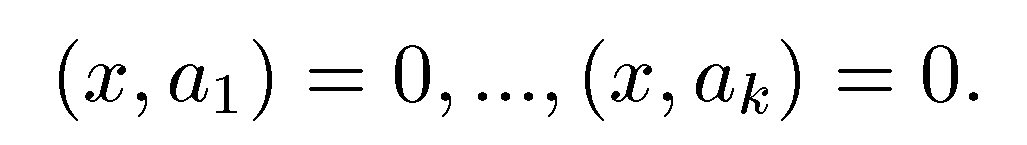 Действительно, если
Действительно, если 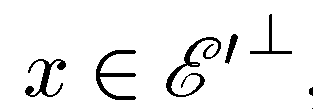 , то равенство
, то равенство 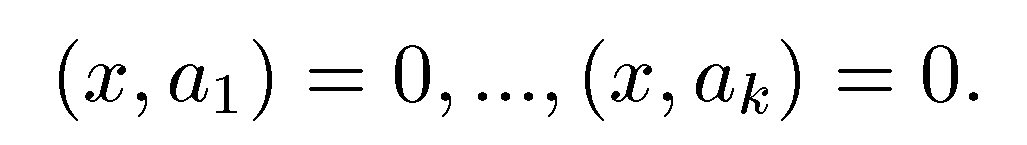 ,разумеется, выполнены. Обратно, при выполнении этих равенств x ортогонален любому a из
,разумеется, выполнены. Обратно, при выполнении этих равенств x ортогонален любому a из  , поскольку
, поскольку
 выберем в
выберем в  ортонормированный базис и обозначим черезь
ортонормированный базис и обозначим черезь 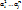 компоненты вектора
компоненты вектора 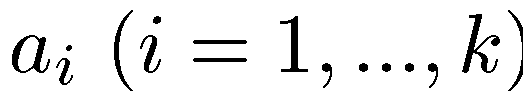 в этом базисе, а через
в этом базисе, а через  - компоненты вектора x. Условия
- компоненты вектора x. Условия 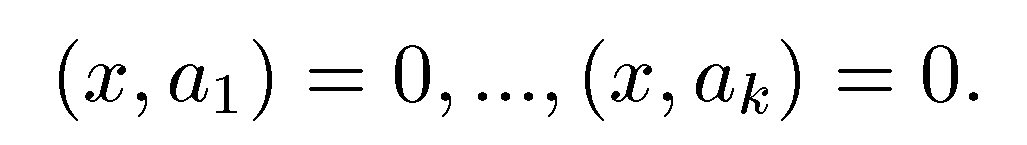 запишутся тогда в виде однородной системы из k линейных уравнений с n неизвестными:
запишутся тогда в виде однородной системы из k линейных уравнений с n неизвестными:
 ранг матрицы системы равен k, поскольку ее строки-строки из компонент векторов
ранг матрицы системы равен k, поскольку ее строки-строки из компонент векторов 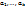 - линейно независимы. Таким образом, множество
- линейно независимы. Таким образом, множество  определяется однородной системой линейных уравнений ранга k, и поэтому является (n-k)-мерным подпространством. Предположении доказаноРассмотрим
определяется однородной системой линейных уравнений ранга k, и поэтому является (n-k)-мерным подпространством. Предположении доказаноРассмотрим 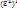 -ортогональное дополнение ортогонального дополнения подпространства
-ортогональное дополнение ортогонального дополнения подпространства  . Каждый вектор из
. Каждый вектор из  ортогонален каждому вектору из
ортогонален каждому вектору из  . Поскольку
. Поскольку 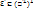 . Но
. Но 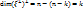 . Итак,
. Итак,  Очевидно, что
Очевидно, что  и
и  не имеют общих ненулевых векторов, а сумма их размерностей равна n. Отсюда следуетЕвклидово пространство-прямая сумма любого своего подпространства и его ортогонального дополнения.Два пространства
не имеют общих ненулевых векторов, а сумма их размерностей равна n. Отсюда следуетЕвклидово пространство-прямая сумма любого своего подпространства и его ортогонального дополнения.Два пространства  и
и  называются ортогональными, если
называются ортогональными, если 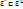 . Тогда
. Тогда  , т.к. (x,y)=0, если
, т.к. (x,y)=0, если 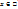 и
и 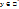

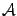 -- линейное преобразование
-- линейное преобразование 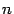 -мерного линейного пространства. Матрица линейного преобразования имеет диагональный вид
-мерного линейного пространства. Матрица линейного преобразования имеет диагональный вид тогда и только тогда, когда векторы базиса являются собственнными векторами преобразования
тогда и только тогда, когда векторы базиса являются собственнными векторами преобразования 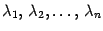 . Следствие Если у матрицы A порядка n существует набор из n линейно независимых собственных векторов, соответствующих собственным числам
. Следствие Если у матрицы A порядка n существует набор из n линейно независимых собственных векторов, соответствующих собственным числам  , то матрица A подобна диагональной матрице с числами
, то матрица A подобна диагональной матрице с числами  преобразования
преобразования  , среди которых нет равных друг другу. Тогда система векторов
, среди которых нет равных друг другу. Тогда система векторов 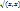 . Углом между векторами x и y назовем каждое число
. Углом между векторами x и y назовем каждое число  , удовлетворяющее условию
, удовлетворяющее условию  В силу аксиомы длина вектора- вещественное неотрицательное число, причем она равна нулю тогда и только тогда, когда вектор нулевой.
В силу аксиомы длина вектора- вещественное неотрицательное число, причем она равна нулю тогда и только тогда, когда вектор нулевой. 
 следует из неравенства Коши-Буняковского:
следует из неравенства Коши-Буняковского: 
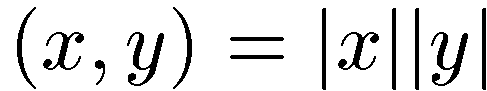 , т.е. если угол между x и y равен нулю, и только в этом случае. Неравенство
, т.е. если угол между x и y равен нулю, и только в этом случае. Неравенство 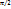 .Только нулевой вектор ортогонален каждому вектору пространства.Действительно, если (x,y)=0 для всех y, то, положив y=x, получим (x,x)=0что возможно только при x=0
.Только нулевой вектор ортогонален каждому вектору пространства.Действительно, если (x,y)=0 для всех y, то, положив y=x, получим (x,x)=0что возможно только при x=0 называется евклидовым, если в нем определена операция скалярного умножения: любым двум векторам x и y из
называется евклидовым, если в нем определена операция скалярного умножения: любым двум векторам x и y из  сопоставлено вещественное число(обозначаемое (x,y)), и это соответствие удовлетворяет сл.требованиям, каковы бы ни были вектора x,y и z и число
сопоставлено вещественное число(обозначаемое (x,y)), и это соответствие удовлетворяет сл.требованиям, каковы бы ни были вектора x,y и z и число  :
: . Любое подпространство
. Любое подпространство  - также евклидово пространство, т.к. для его векторов определено то же самое скалярное умножение. Т.к. (x,
- также евклидово пространство, т.к. для его векторов определено то же самое скалярное умножение. Т.к. (x,  =
=  , имеем (x,
, имеем (x,  Аналогично доказывается
Аналогично доказывается  можно дасть второе определение евклидова пространства, эквивалентное первому. Вещественное линейное пространство называется евклидовым, если в нем задана положительная определенная квадратичная форма. Из первого определения следует второе. Действительно,если в вещественном линейном пространстве определена операция скалярного умножения, то это- функция от двух векторов. Аксиомы 2),3) и формулы(x,
можно дасть второе определение евклидова пространства, эквивалентное первому. Вещественное линейное пространство называется евклидовым, если в нем задана положительная определенная квадратичная форма. Из первого определения следует второе. Действительно,если в вещественном линейном пространстве определена операция скалярного умножения, то это- функция от двух векторов. Аксиомы 2),3) и формулы(x,  число
число  через
через  обозначены элементы столбцов.В пространстве функций, непрерывных на отрезке [0,1], можно ввести скалярное произведение по формуле
обозначены элементы столбцов.В пространстве функций, непрерывных на отрезке [0,1], можно ввести скалярное произведение по формуле  аксиомы вытекают из известных свойств определенных интегралов.
аксиомы вытекают из известных свойств определенных интегралов.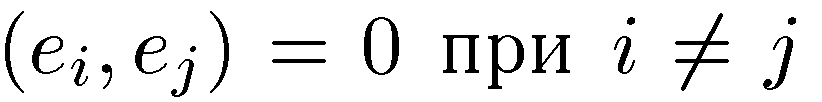
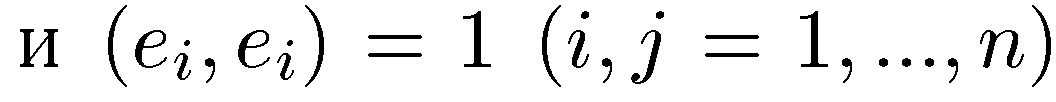 . Это значит, что векторы ортонормированного базиса попарно ортогональны, а по длине равны единице. Для ортонормированного базиса формула
. Это значит, что векторы ортонормированного базиса попарно ортогональны, а по длине равны единице. Для ортонормированного базиса формула  имеет вид:
имеет вид: 
 в n-мерном евклидовом пространстве составляют базис. Разложение вектора по этому базису задается формулой
в n-мерном евклидовом пространстве составляют базис. Разложение вектора по этому базису задается формулой  действительно, матрица из произведений
действительно, матрица из произведений 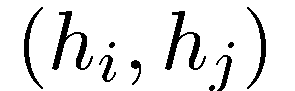 диагональная с ненулевыми элементами на диагонали. Из теоремы следует, что
диагональная с ненулевыми элементами на диагонали. Из теоремы следует, что  . Умножая это равенство скалярно на любой из
. Умножая это равенство скалярно на любой из  , находим, что
, находим, что 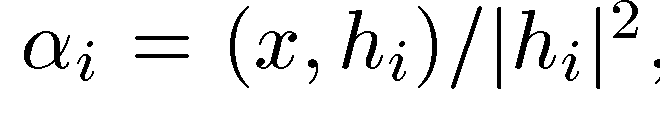 , что равносильно. Базис из ортогональных векторов называется ортогональным базисом. Вычислим (x,x) с помощью формулы
, что равносильно. Базис из ортогональных векторов называется ортогональным базисом. Вычислим (x,x) с помощью формулы  , получаем равенство Парсеваля
, получаем равенство Парсеваля 
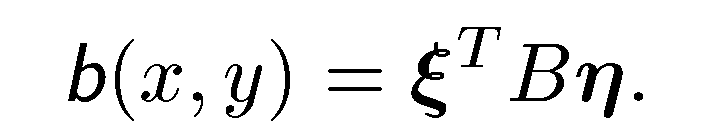 через координатные столбцы
через координатные столбцы 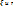 этих векторов:
этих векторов: 
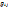 матрицы Г равны скалярным произведениям
матрицы Г равны скалярным произведениям  ,т.е.
,т.е. 
 -произвольная, не обязательно линейно независимая система векторов. Тогда детерминант матрицы, составленной из них попарных скалярных произведений,
-произвольная, не обязательно линейно независимая система векторов. Тогда детерминант матрицы, составленной из них попарных скалярных произведений, 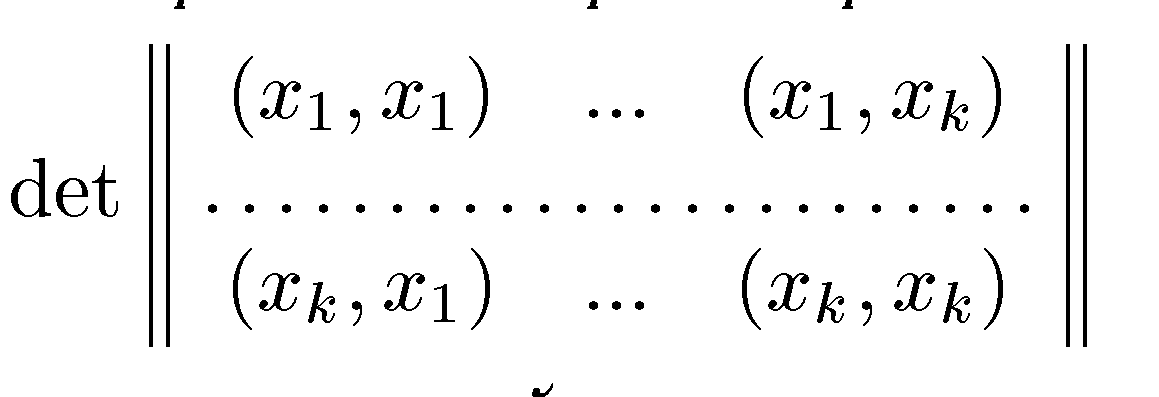 положителен, если векторы линейно независимы, и равен нулю, если они линейно зависимы. Первое утверждение следует из предложения2,т.к. линейно независимые векторы составляют базис в своей линейной оболочке. Докажем второе утверждение. Если вектора линейно зависимые, то выполнено равенство
положителен, если векторы линейно независимы, и равен нулю, если они линейно зависимы. Первое утверждение следует из предложения2,т.к. линейно независимые векторы составляют базис в своей линейной оболочке. Докажем второе утверждение. Если вектора линейно зависимые, то выполнено равенство 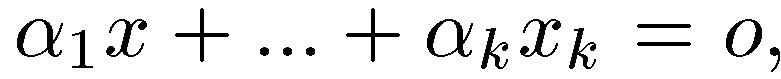 , в котором среди коэффициентов есть отличные от нуля. Умножая это равенство скалярно на каждый из векторов, мы придем к системе линейных уравнений
, в котором среди коэффициентов есть отличные от нуля. Умножая это равенство скалярно на каждый из векторов, мы придем к системе линейных уравнений которой удовлетворяют коэффициент
которой удовлетворяют коэффициент 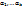 . Т.к. система имеет нетривиальное решение, детерминант ее матрицы равен нулю.
. Т.к. система имеет нетривиальное решение, детерминант ее матрицы равен нулю. связан с базисом e матрицей перехода S. Тогда формула
связан с базисом e матрицей перехода S. Тогда формула  переписывается в виде
переписывается в виде 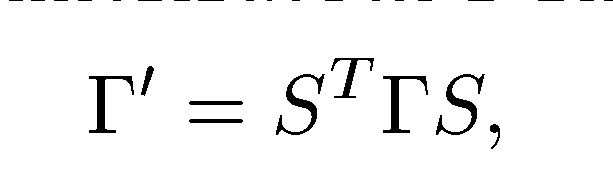 , показывающая связь матрицы Грама двух разных базисов
, показывающая связь матрицы Грама двух разных базисов и
и  . Тогда в формуле (
. Тогда в формуле ( )
)  , и формула принимает вид
, и формула принимает вид 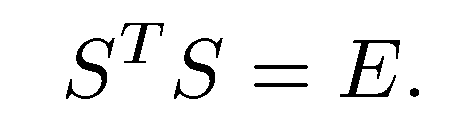
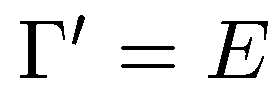 , и новый базис также ортонормированный.
, и новый базис также ортонормированный.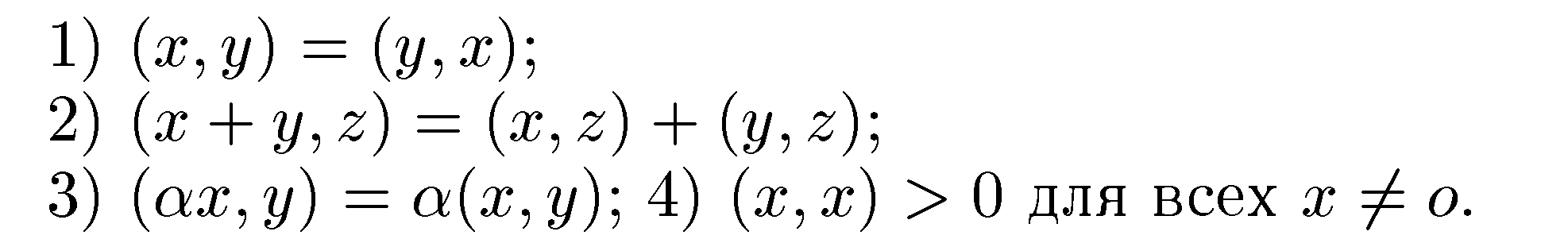 го ортонормированного базиса к другому. Равенство
го ортонормированного базиса к другому. Равенство  из свойств обратной матрицы теперь следует, что
из свойств обратной матрицы теперь следует, что 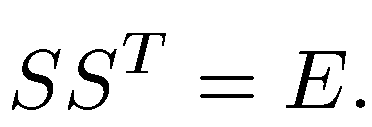 это означает, что матрица
это означает, что матрица 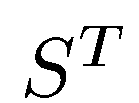 также является ортогональной. Обозначив элементы матрицы S через
также является ортогональной. Обозначив элементы матрицы S через  , мы может написать равенства, равносильные
, мы может написать равенства, равносильные 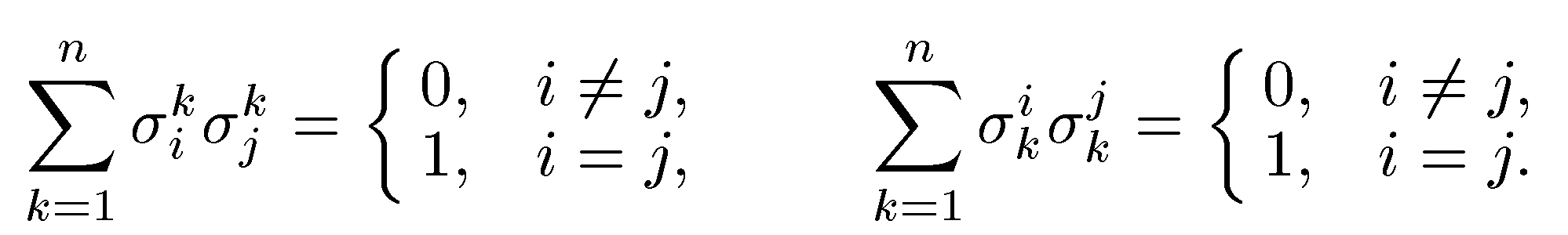 первое из неравенств можно получить непосредственно из
первое из неравенств можно получить непосредственно из  , если вспомнить, что столбцы матрицы перехода - координатные столбцы новых базисных векторов в старом базисе.Произведение SUдвух ортогональных матриц S и U-ортогональная матрица. Действительно,
, если вспомнить, что столбцы матрицы перехода - координатные столбцы новых базисных векторов в старом базисе.Произведение SUдвух ортогональных матриц S и U-ортогональная матрица. Действительно,  . Вычисляя детерминант обеих частей равенства
. Вычисляя детерминант обеих частей равенства 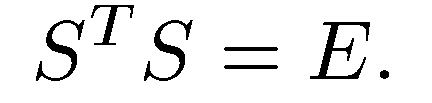 , мы получим
, мы получим 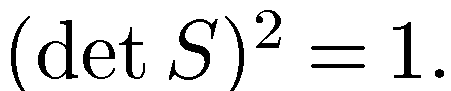 Значит, для ортогональной матрицы
Значит, для ортогональной матрицы 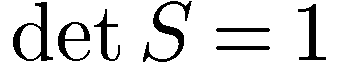 или -1.Любая ортогональная матрица порядка 2 имеет один из двух видов:
или -1.Любая ортогональная матрица порядка 2 имеет один из двух видов:
 - k-мерное подпространство в n-мерном евклидовом пространстве
- k-мерное подпространство в n-мерном евклидовом пространстве  .Ортогональным дополнением подпространства
.Ортогональным дополнением подпространства  .Ортогональное дополнение k-мерного подпространства в n-мерном пространстве есть (n-k)-мерное подпространство.Док-во. Пусть
.Ортогональное дополнение k-мерного подпространства в n-мерном пространстве есть (n-k)-мерное подпространство.Док-во. Пусть  - базис в
- базис в 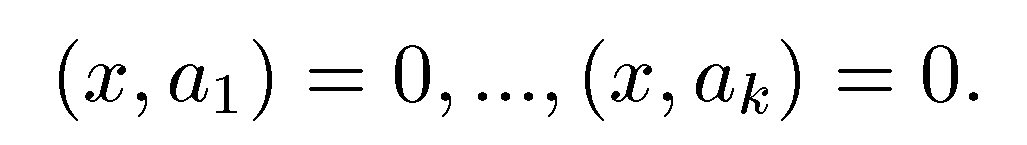 Действительно, если
Действительно, если 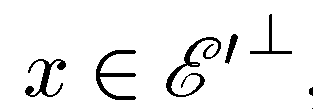 , то равенство
, то равенство  , поскольку
, поскольку выберем в
выберем в 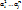 компоненты вектора
компоненты вектора 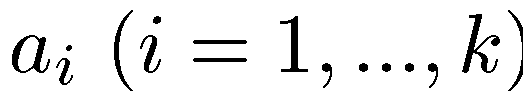 в этом базисе, а через
в этом базисе, а через  - компоненты вектора x. Условия
- компоненты вектора x. Условия  ранг матрицы системы равен k, поскольку ее строки-строки из компонент векторов
ранг матрицы системы равен k, поскольку ее строки-строки из компонент векторов 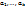 - линейно независимы. Таким образом, множество
- линейно независимы. Таким образом, множество 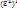 -ортогональное дополнение ортогонального дополнения подпространства
-ортогональное дополнение ортогонального дополнения подпространства  ортогонален каждому вектору из
ортогонален каждому вектору из  . Поскольку
. Поскольку 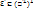 . Но
. Но 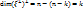 . Итак,
. Итак,  Очевидно, что
Очевидно, что  называются ортогональными, если
называются ортогональными, если 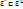 . Тогда
. Тогда  , т.к. (x,y)=0, если
, т.к. (x,y)=0, если 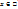 и
и