Свойства векторного произведения.I. [ a * b ] = – [ b * a ] - коллинеарные. II. [a * III .a*b= - b * a – св-во антиперестановочности множителей. III. [ a * b + c ] = [ a * b ] + [ a * c ] - св-во распределенности относительно суммы векторов. 8. Смешанным произведением векторов a, b и c называется число-скаляр, равное скалярному произведению вектора a*b на вектор c:  2. Смешанное произведение не изменится при перемене местами векторного и скалярного произведения: 2. Смешанное произведение не изменится при перемене местами векторного и скалярного произведения:  3. Смешанное произведение меняет знак при перемене мест любых двух векторов-сомножителей: 3. Смешанное произведение меняет знак при перемене мест любых двух векторов-сомножителей: 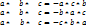 4. Смешанное произведение трех ненулевых векторов равно нулю тогда и только тогда, когда они компланарные: 4. Смешанное произведение трех ненулевых векторов равно нулю тогда и только тогда, когда они компланарные: 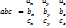 Три вектора называются компланарными, если результат смешанного произведения равен нулю. Три вектора называются компланарными, если результат смешанного произведения равен нулю.
9.
Линейное пространство R, называется евклидовым, если имеется правило, которое позволяет для каждых 2-х векторов x и y из R построить действительное число называемое скалярным произведением векторов x и y и обозначаемые x и y. Для скалярного произведения в действительном и комплексном пространстве справедливо неравенство Буняковского.
10. Для вектора x и y в пространстве Rn называют ортогональный, если их скалярное произведение равно нулю: 11. Матрицей называется прямоугольная таблица чисел. Виды матриц: · Квадратная матрица - если m = n когда число строк = числу столбцов. · Нулевой – если все элементы матрицы = 0. · Главной диагональю квадратичной матрицы - упорядочная совокупность элементов. · Квадратичная матрица - наз. Диагональной, если не 0 –ми является только элементы гл. диагонали. · Единичной матрицей – диагональная матрица, у которой все элементы главной диагонали равны = 0.
12. Действия над матрицами: · Сложение матрицы - сумма матриц А и В – одинакового размера, называется матрица С того же размера каждый которого равен сумме соответствующих элементов матриц А и В. · Умножение матрицы на число – умножение матрицы на действительное число называется матрица, каждый элемент которого получен умножением, соответствующего элемента матрицы А на число альфа. · Св-во операций суммирование и произведение матрицы на число.
13. Определителем второго порядка называется число, полученное с помощью элементов квадратной матрицы 2-го порядка следующим образом: n=2 A При этом из произведения элементов, стоящих на так называемой главной диагонали матрицы (идущей из левого верхнего в правый нижний угол) вычитается произведение элементов, находящихся на второй, или побочной, диагонали. Определителем третьего порядка называется число, определяемое с помощью элементов квадратной матрицы 3-го порядка следующим образом: n =3 A 14. Минором некоторого элемента определителя называется определитель,получаемой из данного определителя вычеркиванием строки и столбца, на пересечении которых расположен этот элемент. Алгебраическим дополнением некоторого элемента определителя называется минор этого элемента, умноженный на -1 в степени Р, где Р - сумма номеров строки и столбца, на пересечение которых расположен этот элемент. Алгебраическое дополнение элемента обозначается такой же прописной буквой, что и сам элемент.
15. Определителем или детерминантом n-го порядка называется число записываемое в виде
Определители n − го порядка вычисляются с помощью метода понижения порядка - по формуле det A =∑ j =1 naijAij (i фиксированно) --- разложение по i −й строке. Из этой формулы и второго свойства определителей - det AT =det A, следует, что верна также формула разложения по j столбцу det A =∑ i =1 naijAij (j фиксированно). 16. Определитель равен сумме произведений элементов какого-нибудь столбца или строки на их алгебраическое дополнение. 17. Матрица B называется обратной для матрицы A, если для них выполняется соотношения А*В=В*А=Е. Для обратной матрицы принято обозначение А в -1 степени. Обратной матрицей А называется матрица А в (-1) степени, если выполняется условие:  det A - это определитель составленный из коофициентов матрицы А a12, a2n – это алгебраические дополнения к элементам матрицы. Обратная матрица может быть найдена единственным способом, для неё выполняется соотношение A*A(-1)=A(-1)*A=E, она очевидна но не для всех, она существует если определитель матрицы А отличен от нуля detA=\0. 18. Элементарные преобразования матрицы det A - это определитель составленный из коофициентов матрицы А a12, a2n – это алгебраические дополнения к элементам матрицы. Обратная матрица может быть найдена единственным способом, для неё выполняется соотношение A*A(-1)=A(-1)*A=E, она очевидна но не для всех, она существует если определитель матрицы А отличен от нуля detA=\0. 18. Элементарные преобразования матрицы Элементарными преобразованиями матрицы называют: 1) умножение какой-нибудь строки (столбца) на отличное от нуля число; 2) прибавление к какой-нибудь строке (столбцу) другой ее строки (столбца), умноженной на произвольное число; 3) перестановку местами любых двух строк (столбцов). Вычисление обратной матрицы. Если с помощью элементарных преобразований строк квадратную матрицу A можно привести к единичной матрице E, то при таких же элементарных преобразованиях над матрицей E получим А в степени -1. Пример:  19. Рангом матрицы называется число ненулевых строк в ступенчатом виде. Ранг матрицы A обозначается r 19. Рангом матрицы называется число ненулевых строк в ступенчатом виде. Ранг матрицы A обозначается r  Ранг матрицы не меняется при элементарных преобразованиях и не зависит от способа приведения матрицы A к ступенчатому виду. 20. Правило Крамара (если система неоднородна, т.е. свободные члены не равны и не равны 0): если d Ранг матрицы не меняется при элементарных преобразованиях и не зависит от способа приведения матрицы A к ступенчатому виду. 20. Правило Крамара (если система неоднородна, т.е. свободные члены не равны и не равны 0): если d 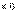 то система имеет одно единственное решение, которое можно найти по формулам Крамара то система имеет одно единственное решение, которое можно найти по формулам Крамара  . В этих формулах . В этих формулах  это определители, полученные из основного определителя заменой соответствующего столбца на столбец свободных членов. Основной определитель системы равен 0, а хотя бы один из определителей это определители, полученные из основного определителя заменой соответствующего столбца на столбец свободных членов. Основной определитель системы равен 0, а хотя бы один из определителей  то система не имеет решений. Определитель равен 0 то система не имеет решений. Определитель равен 0  , бесконечное множество решений. 21. Системой m линейных алгебраических уравнений с n неизвестными называется система вида это совокупность n чисел c1, c2, …, cn, называется решением системы, если при подстановке их в каждое уравнение вместо соответственно неизвестных x1, x2, …, xn все уравнения системы обращаются в тождества. Система уравнений называется совместной, если она имеет хотя бы одно решение. Если система решений не имеет, то она называется несовместной. Теперь можно записать систему в матричной форме A · X = B. Векторная форма системы имеет вид: x1 A1 + x2 A2 + … + xn An = B - здесь A1, A2, …, An — столбцы матрицы A. Теорема Кронекера–Капелли (условие совместности системы уравнений). Для того, чтобы система линейных уравнений была совместна, необходимо и достаточно, чтобы ранг ее основной матрицы был равен рангу расширенной матрицы. 22. Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные. Здесь описан алгоритм решения системы линейных уравнений с помощью так называемого метода Гаусса. Программу вы можете скачать разделе программы. Алгоритм реализован на языке С.Пусть у нас есть система N линейных уравненийa11x1 + a12x2 + a13x3 +... a1NxN = b1 , бесконечное множество решений. 21. Системой m линейных алгебраических уравнений с n неизвестными называется система вида это совокупность n чисел c1, c2, …, cn, называется решением системы, если при подстановке их в каждое уравнение вместо соответственно неизвестных x1, x2, …, xn все уравнения системы обращаются в тождества. Система уравнений называется совместной, если она имеет хотя бы одно решение. Если система решений не имеет, то она называется несовместной. Теперь можно записать систему в матричной форме A · X = B. Векторная форма системы имеет вид: x1 A1 + x2 A2 + … + xn An = B - здесь A1, A2, …, An — столбцы матрицы A. Теорема Кронекера–Капелли (условие совместности системы уравнений). Для того, чтобы система линейных уравнений была совместна, необходимо и достаточно, чтобы ранг ее основной матрицы был равен рангу расширенной матрицы. 22. Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные. Здесь описан алгоритм решения системы линейных уравнений с помощью так называемого метода Гаусса. Программу вы можете скачать разделе программы. Алгоритм реализован на языке С.Пусть у нас есть система N линейных уравненийa11x1 + a12x2 + a13x3 +... a1NxN = b1 a21x1 + a22x2 + a23x3 +... a2NxN = b2 a31x1 + a32x2 + a33x3 +... a3NxN = b3 ... aN1x1 + aN2x2 + aN3x3 +... aNNxN = bN , где xi - неизвестные, aij - коэффициенты при неизвестных, bi - свободные члены в уравнениях, i,j пробегают значения от 1 до N. Цель задачи - зная aij и bi найти xi. Суть метода Гаусса состоит в том, что с помощью некоторых операций исходную систему уравнений можно свести к более простой системе. Эта простая система имеет треугольный вид:
 . Если система к треугольному виду не привилась т.е остаётся ступенчатый вид, то она имеет бесконечное множество решений. Для однородной системы линейных уравнений при решении методом гаусса если число уравнений меньше числанеизвестных то система имеет не нулевое решение. 23. Система однородных уравнений всегда имеет нулевое решение. Если ранг матрицы меньше числа неизвестных, то система имеет бесчисленное множество решений. Для тог, чтобы система имела ненулевые решения, необходимо, чтобы ее определитель был равен нулю. 24. Матрицу А называют ступенчатой, если: . Если система к треугольному виду не привилась т.е остаётся ступенчатый вид, то она имеет бесконечное множество решений. Для однородной системы линейных уравнений при решении методом гаусса если число уравнений меньше числанеизвестных то система имеет не нулевое решение. 23. Система однородных уравнений всегда имеет нулевое решение. Если ранг матрицы меньше числа неизвестных, то система имеет бесчисленное множество решений. Для тог, чтобы система имела ненулевые решения, необходимо, чтобы ее определитель был равен нулю. 24. Матрицу А называют ступенчатой, если: А) любая ее строка имеет хотя бы один отличный от нуля элемент, Б) первый отличный от нуля элемент каждой ее строки, начиная со второй, расположен правее неравного нулю элемента предыдущей строки. Метод Гаусса является эффективным методом решения и исследования систем линейных уравнений. Он состоит в том, что данная система линейных уравнений преобразуется в равносильную ей систему ступенчатого вида, которая легко решается и исследуется. Применение метода Гаусса не зависит ни от числа уравнений, ни от числа неизвестных в системе. 25. Если ранг матрицы А, равен r, то любой отличный от нуля минор порядка r этой матрицы называется базисным. пример
26. Геометрическая интерпретация систем линейных уравнений в случае двух или трех неизвестных Если каждое решение линейного уравнения относительно двух неизвестных ax+by+c = 0, в котором коэффициенты при неизвестных не равны нулю одновременно, изображать точкой плоскости с координатами (x, y), то множество всех таких точек образует некоторую прямую. Поэтому множеству решений системы из двух таких уравнений соответствует множество точек пересечения двух прямых. Система несовместна, если прямые параллельны; имеет единственное решение, если прямые пересекаются; имеет бесконечное множество решений, если прямые совпадают. Множество точек пространства, соответствующих решениям линейного уравнения относительно трех неизвестных ax+by+cz+d = 0, в котором коэффициенты при неизвестных не равны нулю одновременно, является некоторой плоскостью Система из трех таких уравнений определяет множество точек пересечения этих плоскостей. Возможные при этом случаи изображены на предыдущем рисунке. 27. Ненулевые решения однородной системы уравнений Система уравнений называется однородной, если все ее правые части равны нулю. Однородная система всегда имеет решение, например, нулевую строку. Поэтому интересно выяснить, когда имеются и ненулевые решения. Теорема (о ненулевых решениях однородной системы уравнений). Если число уравнений однородной системы линейных уравнений меньше числа неизвестных, то существуют ненулевые решения. Доказательство. Приведем данную однородную систему к ступенчатому виду. Разумеется, она останется однородной. Ясно, что число главных неизвестных не может превысить числа строк. Следовательно, существуют свободные неизвестные, что обеспечивает существование ненулевых решений. 28. 29. 30. Линейный оператор A действует из n-мерного линейного пространства X в m-мерное линейное пространство Y. В этих пространствах определены базисы e = {e1,..., en} и f = {f1,..., fm}. Пусть A(ei) = a1i·f1 + a2i·f2 +...+ ami·fm — разложение образа i-го базисного вектора базиса e пространства X по базису f пространства Y, i = 1, 2,..., n. Матрицей линейного оператора в базисах e, f называется матрица A, столбцами которой являются координаты образов базисных векторов базиса e в базисе f, A = {aij}= {A(ej)i}:
32. Таким образом, можно описать алгоритм приведения матрицы линейного оператора к диагональной форме. Он состоит в следующем: · записываем матрицу оператора A в исходном базисе; · записываем характеристическое уравнение и вычисляем его корни; · находим собственный базис оператора (если он существует); · записываем матрицу C, столбцами которой являются координаты собственных векторов (векторов собственного базиса); · по формуле C-1AC находим диагональную форму матриц оператора — матрицу оператора в собственном базисе. Нормальную (в частности симметричную) матрицу A можно привести к диагональному виду преобразованием подобия — A = TΛT−1 Здесь Λ = diag(λ1,..., λ N) — это диагональная матрица, элементами которой являются собственные значения матрицы A, а T — это матрица, составленная из соответствующих собственных векторов матрицы A, т.е. T = (v1,...,v N). 33. Пусть A^: Xn → Xn — линейный оператор. 1. Все собственные векторы линейного оператора, соответствующие одному и тому же собственному значению, вместе с нулевым вектором образуют линейное пространство. 2. Собственные векторы линейного оператора, соответствующие различным собственным значениям, линейно независимы. 3. Если линейный оператор A^: Xn → Xn имеет n различных (вещественных) собственных значений, то собственные векторы, соответствующие этим собственным значениям, образуют базис в Xn. Такой базис называется собственным базисом линейного оператора A^. 4. Матрица A линейного оператора A^: Xn → Xn в некотором базисе x1, x2, …, xn имеет диагональный вид тогда и только тогда, когда этот базис собственный, причем диагональные элементы этой матрицы — собственные значения оператора λ1, λ2, …, λn. 34.Линейный функционал — функционал, обладающий свойством линейности по своему аргументу:
Иными словами, это линейное отображение из (некоторого) пространства функций во множество чисел — чаще всего подразумеваемых вещественными, или, еще иначе, линейный оператор, действующий из (некоторого) пространства функций в Выделяют следующие специальные виды функционалов: · интегральный: · терминальный: · смешанный (функционал Больца):
35. Пусть e1,..., e n — базис в L. И пусть для векторов x и y из L заданы разложения x = x 1·e1+ x 2·e2+...+ xn · e n и y = y 1·e1+ y 2·e2+...+ yn · e n. Тогда для билинейной формы φ(x, y) справедливо представление Обозначим φ i j = φ(ei , ej). Тогда для билинейной формы формы φ(x, y) справедливо матричное представление φ(x, y) = x T·Φ·y:
Матрица Φ называется матрицей билинейной формы. Ранг матрицы билинейной формы не зависит от выбора базиса и называется рангом билинейной формы. Дефектом билинейной формы называется разность между размерностью пространства и рангом билинейной формы: d = n − r. Билинейная форма называется невырожденной, если её дефект равен нулю. 36. Пусть X — линейное пространство. Функция b(x,y), осуществляющая отображение X × X → R, называется билинейной формой, если она линейна по каждому аргументу, т.е. " x, y, z О X и " α, β О R
Билинейная форма называется симметричной, если " x, y О X b(x, y) = b(y, x). Пусть e1, e2, …, en — базис в Xn. Тогда " x,y О Xn X= Обозначим bij = b(ei, ej). Воспользовавшись линейностью b(x, y) по обоим аргументам, получим:
Квадратная матрица n –го порядка B = (bij) называется матрицей билинейной формы. Обозначив X и Y координатные столбцы векторов x и y, билинейную форму можно записать в виде:
Преобразование матрицы билинейной формы при переходе к новому базису. Пусть в Xn базисы e1, e2, …, en и f1, f2, …, fn связаны матрицей перехода C = (cik) по формуле Обозначим Be и Bf матрицы билинейной формы b(x,y) в базисах e1, e2, …, en и f1, f2, …, fn соответственно. Тогда
Справедливы следующие утверждения. Матрица симметричной билинейной формы симметрична в любом базисе. Если матрица билинейной формы симметрична в некотором базисе, то билинейная форма симметрична.
37. Матрица, представляющая билинейную форму в новом базисе, связана с матрицей, представляющей её в старом базисе, через матрицу, обратную матрице перехода к новому базису (матрице Якоби), через которую преобразуются координаты векторов. Иными словами, если координаты вектора в старом базисе Xi выражаются через координаты в новом xi через матрицу
то есть компоненты матрицы, представляющей билинейную форму в новом базисе, будут:
или, в матричной записи:
38. Квадратичная форма — функция на векторном пространстве, задаваемая однородным многочленом второй степени от координат вектора. Пусть 39. Критерий Сильвестра положительной определенности квадратичной формы. Доказательство критерия Сильвестра основано на методе Якоби приведения квадратичной формы к каноническому виду. Для положительной определённости квадратичной формы необходимо и достаточно, чтобы главные миноры её матрицы были положительны. 1. «Необходимо.» Имеется положительно определённая квадратичная форма. j-ый диагональный элемент положителен, так как k(x)>0 в том числе и для вектора со всеми нулевыми координатами, кроме j-ой. При приведении матрицы к каноническому виду не будет нужно переставлять строки, и знаки главных миноров матрицы не изменятся. А в каноническом виде диагональные элементы положительны, и миноры положительны; следовательно, (так как их знак не менялся при преобразованиях), у положительно определённой квадратичной формы в любом базисе главные миноры матрицы положительны. 2. «Достаточно.» Имеется положительность миноров. Первый минор определяет знак первого диагонального элемента в каноническом виде. Знак отношения Mi+1/Mi определяет знак i+1-ого элемента в диагональном виде. Так получим, что в каноническом виде все элементы на диагонали положительные, то есть квадратичная форма определена положительно.
|

 b ] =
b ] = 
 .
.


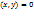
 det A= a11* a22 - a12 *a21
det A= a11* a22 - a12 *a21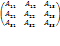

 и вычисляемым по данным числам
и вычисляемым по данным числам  (действительным или комплексным) — элементам определителя – по следующему закону:
(действительным или комплексным) — элементам определителя – по следующему закону:  есть сумма
есть сумма 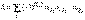 , распространенная на всевозможные различные перестановки
, распространенная на всевозможные различные перестановки  из чисел 1, 2, …, n. Число t от j равно числу транспозиций, которые нужно сделать, чтобы перейти от основной перестановки 1, 2, …, n к перестановке
из чисел 1, 2, …, n. Число t от j равно числу транспозиций, которые нужно сделать, чтобы перейти от основной перестановки 1, 2, …, n к перестановке  . Произведение
. Произведение  называется членом определителя.
называется членом определителя. Решение. Выпишем расширенную матрицу системы и приведем ее к виду, когда ниже главной диагонали будут стоять нули.
Решение. Выпишем расширенную матрицу системы и приведем ее к виду, когда ниже главной диагонали будут стоять нули.  Получим нули в первом столбце матрицы, для чего умножим первую строку на -2 и прибавим ко второй, а затем первую строку умножим на -1 и прибавим к последней строке. Имеем
Получим нули в первом столбце матрицы, для чего умножим первую строку на -2 и прибавим ко второй, а затем первую строку умножим на -1 и прибавим к последней строке. Имеем  Прибавим теперь вторую строку к третьей и к четвертой. Тогда
Прибавим теперь вторую строку к третьей и к четвертой. Тогда 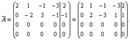 -
-  Система совместна. Выпишем укороченную систему, полученную после преобразований:
Система совместна. Выпишем укороченную систему, полученную после преобразований: 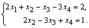 Эта система имеет бесчисленное множество решений, так как ранг матрицы меньше числа неизвестных. Выберем в преобразованной матрице базисный минор. Это
Эта система имеет бесчисленное множество решений, так как ранг матрицы меньше числа неизвестных. Выберем в преобразованной матрице базисный минор. Это 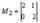 Тогда неизвестные Х1 и Х2 будут базисными, а остальные – свободными. Свободные неизвестные перенесем в правую часть уравнений системы:
Тогда неизвестные Х1 и Х2 будут базисными, а остальные – свободными. Свободные неизвестные перенесем в правую часть уравнений системы:  Ясно, что базисные неизвестные зависят от того, какие значения имеют свободные неизвестные Х3 и Х4 Обозначим
Ясно, что базисные неизвестные зависят от того, какие значения имеют свободные неизвестные Х3 и Х4 Обозначим  где С1 и С2 – это произвольные значения свободных неизвестных, т. е. любые числа. Тогда укороченная система имеет вид
где С1 и С2 – это произвольные значения свободных неизвестных, т. е. любые числа. Тогда укороченная система имеет вид  Из второго уравнения находим
Из второго уравнения находим  Подставим найденное Х2 в первое уравнение:
Подставим найденное Х2 в первое уравнение: 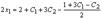 и
и Таким образом, решение системы, которое в данном случае называют общим, имеет вид
Таким образом, решение системы, которое в данном случае называют общим, имеет вид 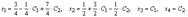
 Координаты образа y = A(x) и прообраза x связаны соотношеннием: y = A · x,
Координаты образа y = A(x) и прообраза x связаны соотношеннием: y = A · x,  ;
; 
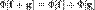 ;
;  , где Ф — линейный функционал, f и g — функции из его области определения, c — число (константа).
, где Ф — линейный функционал, f и g — функции из его области определения, c — число (константа). (иногда в
(иногда в  ).
).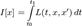

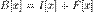
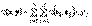
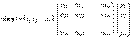 ;
; 
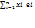 ; y=
; y= 

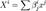 , или в матричной записи
, или в матричной записи  , то билинейная форма F на любых векторах
, то билинейная форма F на любых векторах  и y запишется, как
и y запишется, как ,
, ,
, ,
, 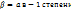 , где
, где  — матрица прямого преобразования координат x = aX.
— матрица прямого преобразования координат x = aX. есть векторное пространство над полем
есть векторное пространство над полем  и
и  — базис в L. Функция Q:L
— базис в L. Функция Q:L  K называется квадратичной формой, если её можно представить в виде
K называется квадратичной формой, если её можно представить в виде 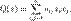 , где
, где  , а
, а 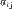 — некоторые элементы поля K. Квадратичные формы.
— некоторые элементы поля K. Квадратичные формы.  . Замена базиса в данном случае очевидным образом следует из замены базиса в билинейной форме.
. Замена базиса в данном случае очевидным образом следует из замены базиса в билинейной форме.


