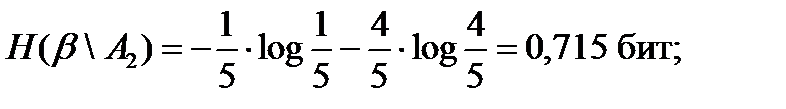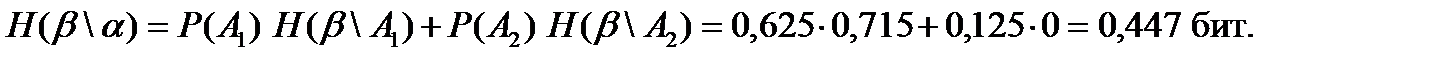Задачи для самостоятельной работыЗадача 10.1. Алфавит состоит из 10 букв: А 1, А 2,…, А 10 с вероятностями появления в сообщении соответственно: р 1=0,3; р 2=0,25; р 3=0,25; р 4=0,1; р 5=0,05; р 6=0,02; р 7=0,01; р 8=0,01; р 9=0,005; р 10=0,005. Осуществить кодирование данного алфавита методами Хаффмена и Шеннона – Фано, и сравнить экономичность полученных кодов. Задача 10.2. Осуществить кодирование вышеуказанного алфавита при следующем распределении вероятностей: р 1=0,2; р 2=0,2; р 3=0,1; р 4=0,1; р 5=0,1; р 6=0,1; р 7=0,05; р 8=0,05; р 9=0,05; р 10=0,05. Сопоставить результаты кодирования. Сделать выводы.
Решения и ответы задач для самостоятельной работы Решение задачи 1.1. В корзине 100 шаров белого, черного и красного цвета. В соответствии с этим количество возможных исходов выемки одного шара определенного цвета определяется множеством 1) 2) для подмножества черных шаров 3) для подмножества красных шаров Ответ:{0,2; 0,3; 0,5}. Решение задачи 1.2. В студенческой группе 22 человека. В соответствии с этим количество возможных исходов отсутствия определенного числа студентов определяется множеством 1) 2) для подмножества девушек 3) для подмножества юношей Задача решена по схеме урн (смотрите пример 1.3). Ответ: { Решение задачи 1.3. В году 365 дней. В соответствии с этим количество возможных ухудшений погоды определяется множеством 1) 2) Задача также решается по схеме урн. Ответ: { Решение задачи 1.6. Общее число попаданий при стрельбе по мишени n =48 (рисунок 0.1) определяет число испытаний для определения апостериорной вероятности.
Рисунок 0.1. – Иллюстрация мишени Из рисунка 0.1 видно, что вероятность того, что цель была поражена одним выстрелом, если по своим размерам она была меньше 10, не определена. Вероятности того, что цель была поражена одним выстрелом, если по своим размерам она была меньше 9, 8, 7, 6,…,0; соответственно равны:
Таким образом, при уменьшении Ответ:{ Решение задачи 2.1. Из 40 вопросов можно выбрать два вопроса С 240 способами. Из 40–8=32 вопросов – два вопроса, на которые студент знает ответ, можно выбрать С 232 способами. Пусть Р(А) – вероятность того, что студент вытянет два вопроса, на которые он знает ответ
Р(В) – вероятность того, что студент только знает один ответ из двух вопросов билета
Тогда вероятность сдачи зачета
так как события А и В несовместные. Искомая вероятность
Ответ:0,715. Решение задачи 2.2. События выхода из строя R и С совместные. Поэтому искомая вероятность определится формулой
Ответ:0,325. Решение задачи 2.3. Существует два способа решения этой задачи. Первый способ. Обозначим
Тогда по формуле сложения вероятностей получим
Второй способ. Обозначим через
Ответ: 0,47. Решениезадачи 2.4. Пусть А – событие наличия файлов данных в каталоге: P(A)= 0,85; B\A – событие того, что файлы данных защищены: Р(В\А) =0,8. Тогда событие В того, что наудачу взятый файл будет защищенным, определяется по формуле
Ответ:0,68. Решение задачи 2.5. Обозначим: событие Из условия задачи находим вероятности событий до и после опыта – перемещения документа из первой папки во вторую:
По формуле полной вероятности вычисляем
Ответ:0,014. Решение задачи 2.6. Пусть событие А состоит в том, что один из трех студентов дал правильный ответ. До ответа на вопрос преподавателя возможны следующие события (гипотезы), совместные с А:
Применяя теорему умножения вероятностей для независимых событий, получим
По формуле Байеса определяем вероятность того, что был вызван второй студент
Ответ:0,18. Решение задачи 2.7. Из 30 вопросов можно выбрать два Пусть Р(А) – вероятность того, что студент вытянет два вопроса, на которые знает ответ
Р(В) – вероятность того, что студент вытянет один вопрос, на который знает ответ
Тогда вероятность сдачи зачета
так как события А и В несовместные. Искомая вероятность равна
Аналогичным образом определяется вероятность сдачи зачета в случае, когда студент должен ответить на два вопроса из трех заданных
Ответ: {0,8; 0,77}. Вероятность сдачи зачета во втором случае уменьшится. Решение задачи 3.1. а). Гистограмма строится следующим образом (Рисунок 0.2).
Рисунок 0.2 – Гистограмма
По оси абсцисс откладываются разряды Ik, и на каждом из разрядов, как на основании, строится прямоугольник, площадь и высота которого равны вероятности pk данного разряда в случае, когда длины Площадь гистограммы равна
Поэтому в пределе площадь гистограммы стремится к единице
б) Составим таблицу для функции распределения ошибки наводки Таблица – Функция распределения ошибки наводки
Функция распределения ошибки наводки F(k) показана на Рисунке 0.3.
Рисунок 0.3.– Функция распределения
Ответ:Площадь гистограммы в пределе стремится к единице и равна 0,998. Решение задачи 4.1. Случайная величина Z соответствует событию попадания и может принимать значения {0,1,2,3,4,5}. Вероятность попадания P (Z=zi) вычисляется по формуле Бернулли:
Используя формулу Бернулли, вычислим вероятности Составим ряд распределений (таблица 0.1) Таблица 0.1 – Ряд распределения попадания в мишень
Построим график функции распределения (Рисунок 0.4).
Рисунок 0.4 – Функция распределения Математическое ожидание, дисперсия и СКО случайной величины Z соответственно равны:
Ответ:{2; 1,203; 1,097}. Решение задачи 4.2. Вероятность брака полупроводниковых изделий равна p =0,1; число изделий – n =40. Так как число полупроводниковых изделий велико, то целесообразно применить закон Пуассона (формула (4.9))
где Тогда вероятность брака 5 изделий будет равна
Ответ: 0,168. Решение задачи 4.3. Сбой ЭВМ за короткое время является редким событием. Поэтому здесь применим закон Пуассона
где а). Определим вероятность того, что в течении ½ часа не пройдет ни одного сбоя. Число возможных сбоев равно
б). Определим вероятность того, что в течении ½ часа пройдет один сбой
в). Определим вероятность того, что в течении ½ часа пройдет два сбоя
Ответ:{0,135; 0,27; 0,27}. Решение задачи 5.1. 1). Сложив вероятности по столбцам, получим вероятности возможных значений веса X (таблица 0.2):
Контроль:
Таблица 0.2 – Закон распределения рабочих циклов двигателя
Сложив вероятности по строкам, получим вероятности возможных значений веса Y (таблица 0.3):
Контроль:
Таблица 0.3 – Закон распределения пробега автомобиля
2). Определим числовые характеристики системы (X, Y): 1. Математические ожидания случайных величин X и Y определяются через суммирование по строкам и столбцам вероятностей
2. Дисперсия СВ X:
3. Дисперсия СВ Y:
4. Средние квадратичные отклонения:
5. Ковариация СВ X и Y:
6. Коэффициент корреляции:
Ответ:2) {2,254, 2,001; 0,64, 0,667; 0,8, 0,8167; 0,0559; 0,0856}. Решение задачи 5.2. Определим числовые характеристики системы (X, Y): 1. Математические ожидания случайных величин X и Y определяются через суммирование по строкам и столбцам вероятностей
2. Дисперсия СВ X:
3. Дисперсия СВ Y:
4. Средние квадратичные отклонения:
5. Ковариация СВ X и Y:
6. Коэффициент корреляции:
Ответ: {159,6, 74,4; 190,96, 24,64; 13,8188, 4,9639; 9,9296; 0,1448}. Решение задачи 5.3. Корреляционная матрица в нашем случае имеет структуру (5.6)
где
Другие ковариации равны Нормированная корреляционная матрица формируется через коэффициенты корреляции между СВ Xi и Xj
Поэтому
Учитывая симметричность матрицы K:
Решение задачи 7.1. Ход решения задачи 7.1 соответствует содержанию примера 7.2 с другими условиями: r =0,2; q =0,1. MatLab – программа представлена в Приложении 1. Ответ: Решение задачи 7.2. Для составления СЛАУ воспользуемся формулой (7.7)
с исключенным первым узлом
После преобразований получим СЛАУ AX=B:
Протокол решения СЛАУ (программа в М-файле MatLab) имеет вид:
MatLab – программа представлена в Приложении 1. Ответ: Решение задачи 7.3. Составим граф состояний в период обучения, считая, что в случае неуспешной сдачи летней сессии студент может восстановиться на этом же курсе (Рисунок 0.5).
Вероятность несдачи экзаменов в летней сессии Тогда вероятности перехода с одного курса на другой курс равны: Последняя группа финальных вероятностей ( Искомая матрица переходов:
Решение задачи 8.1. Во всех трех случаях для вычисления энтропии используется формула (8.1). MatLab – программа для вычисления энтропии при неравновероятном распределении букв алфавита представлена в Приложении 2. Ответ:Энтропия максимальна в случае равновероятного распределения букв русского алфавита. С увеличением числа страниц книги апостериорные вероятности (частоты появления букв) стремятся к априорным вероятностям распределения букв алфавита, приведенных в таблице 1.1, то есть в пределе энтропии в последних двух случаях будут равны между собой. Решение задачи 8.2. Определение той или иной болезни к болезни А представим как опыт β;, имеющий два возможных исхода: В1 – не относится; В 2 – относится. Определение эффективности системы диагностики (СД) представим как опыт α;, также имеющий два возможных исхода: А 1 – определен признак А; А 2 – не определен признак А. Вероятности определения и неопределения признака В соответственно равны:
Неопределенность отношения той или иной болезни к А:
Это есть неопределенность СД по отношению к болезни А. В целом, с учетом эффективности работы системы диагностирования, то есть опыта α;, неопределенность СД можно вычислить через условную энтропию Н(α\β;). Для этого определим: 1). Условные вероятности исходов В 1 и В 2 опыта β; при условии исходов А 1 и А 2 опыта α;:
так как из 25 случаев, когда система диагностики давала положительный ответ, в 20 случаях не подтверждалась болезнь А, а в 5 случаях подтверждалась,
2). Условные энтропии системы диагностики (при условиях А 1 и А 2):
Тогда средняя условная энтропия опыта β; (эффективность системы диагностирования) при условии существования СД (опыт α) равна:
Ответ: СД имеет относительно высокую эффективность, так как снимает неопределенность на 35,6 %. Решение задачи 9.1. Ход решения задачи 9.1 повторяет содержание примеров 9.1 и 9.2. MatLab – программа представлена в Приложении 3. Решение задач 10.1 и 10.2. Ход решения задач повторяет содержание примеров 10.2 и 10.4. Алгоритмы построения кодов Хаффмена и Шеннона–Фано приведены в Приложении 4.
Дополнительные задачи по курсу «Теория информации»
|

 . Поскольку все исходы равновероятны, то выемке одного шара соответствует вероятность
. Поскольку все исходы равновероятны, то выемке одного шара соответствует вероятность  Тогда
Тогда для подмножества белых шаров
для подмножества белых шаров  вероятность выемки белого шара будет
вероятность выемки белого шара будет 
 вероятность выемки черного шара будет
вероятность выемки черного шара будет 
 вероятность выемки красного шара будет
вероятность выемки красного шара будет 
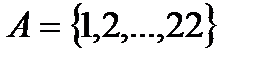 . Поскольку все исходы равновероятны, то отсутствию на семинаре одного студента соответствует вероятность
. Поскольку все исходы равновероятны, то отсутствию на семинаре одного студента соответствует вероятность  Тогда
Тогда вероятность отсутствия на семинаре 1 юноши из группы юношей будет
вероятность отсутствия на семинаре 1 юноши из группы юношей будет 
 вероятность отсутствия на семинаре 1 девушки из группы девушек равна
вероятность отсутствия на семинаре 1 девушки из группы девушек равна 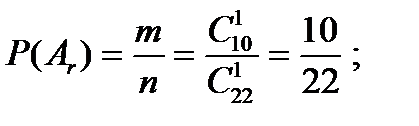

 }.
}. . Поскольку все исходы равновероятны, то выпадению дождя или снега соответствует вероятность
. Поскольку все исходы равновероятны, то выпадению дождя или снега соответствует вероятность 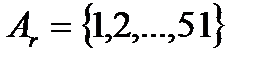 вероятность выпадения осадков, когда вы идете на работу, будет
вероятность выпадения осадков, когда вы идете на работу, будет 

 }.
}.

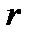 от 10 до 1 апостериорная вероятность попадания одним выстрелом по мишени стремится к априорной вероятности:
от 10 до 1 апостериорная вероятность попадания одним выстрелом по мишени стремится к априорной вероятности: 
 }.
}.


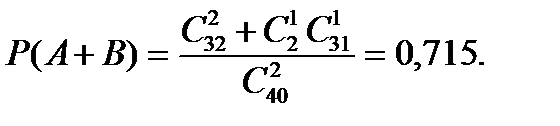

 как событие удачного звонка абонента не более чем с четвертого раза; через
как событие удачного звонка абонента не более чем с четвертого раза; через  – событие, что абонент угадал последнюю цифру телефона с первого раза;
– событие, что абонент угадал последнюю цифру телефона с первого раза; 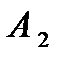 – со второго раза;
– со второго раза;  – с третьего раза;
– с третьего раза; 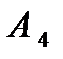 – с четвертого раза. Поскольку события набора последней цифры телефона 0, 1,…, 9 независимые, то вероятности этих событий равны:
– с четвертого раза. Поскольку события набора последней цифры телефона 0, 1,…, 9 независимые, то вероятности этих событий равны:



 – незарегистрированный документ принадлежит первой папке; событие
– незарегистрированный документ принадлежит первой папке; событие  – незарегистрированный документ принадлежит второй папке; событие
– незарегистрированный документ принадлежит второй папке; событие 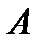 – незарегистрированный документ извлечен из второй папки.
– незарегистрированный документ извлечен из второй папки.




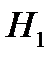 – вызван для ответа первый студент;
– вызван для ответа первый студент; – вызван для ответа второй студент;
– вызван для ответа второй студент; – вызван для ответа третий студент.
– вызван для ответа третий студент. :
:
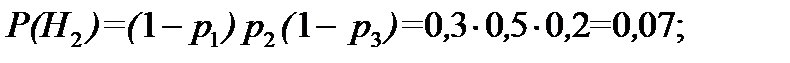

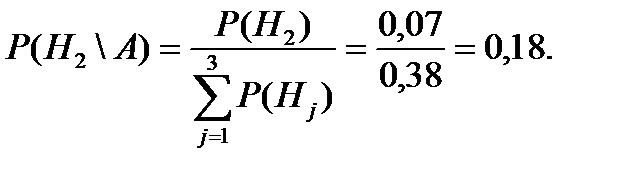
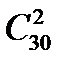 способами. Из 30–5=25 вопросов – вопросы, на которые студент знает ответ, можно выбрать
способами. Из 30–5=25 вопросов – вопросы, на которые студент знает ответ, можно выбрать  способами
способами


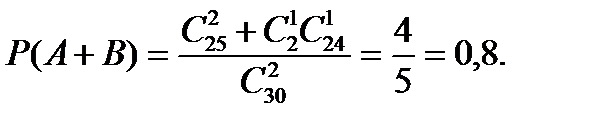



 равны единице.
равны единице.














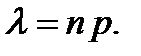
 ; вероятность сбоя – p =0,01. Поэтому
; вероятность сбоя – p =0,01. Поэтому  Тогда
Тогда






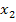

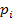







 в таблице 5.5
в таблице 5.5




















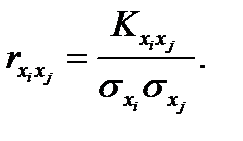

 =
=  сформируем нормированную корреляционную матрицу
сформируем нормированную корреляционную матрицу
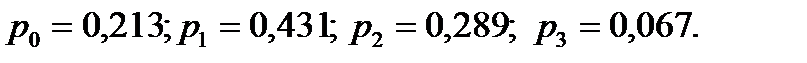



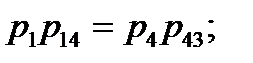
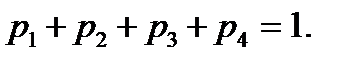






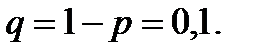


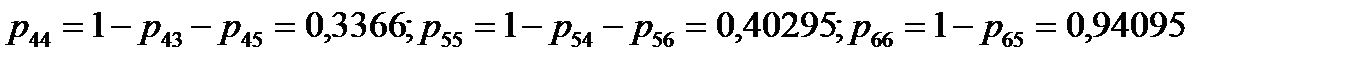 .
. ) определяется согласно свойству цепи Маркова:
) определяется согласно свойству цепи Маркова: 


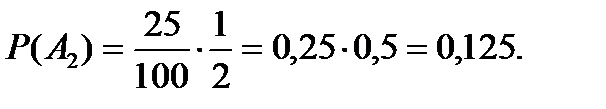


 .
.