Факультет ЭМСиТВариант № 0. Задание 1. Найти пределы функций. а) в) д) Задание 2. Найти производные заданных функций. а) в) Задание 3. Исследовать средствами дифференциального исчисления функцию Задание 4. Найти неопределенные интегралы. а) в) Задание 5. Вычислить определенные интегралы по формуле Ньютона- Лейбница. а) Задание 6. Найти обшее решение дифференциального уравнения
удовлетворяющее начальным условиям х0=0, у0=0. Задание 7. Написать три первых члена ряда по заданному общему члену
исследовать сходимость ряда на концах интервала.
Вариант № 1. Задание 1. Найти пределы функций. а) в) д) Задание 2. Найти производные заданных функций. а) в) Задание 3. Исследовать средствами дифференциального исчисления функцию Задание 4. Найти неопределенные интегралы. а) в) Задание 5. Вычислить определенные интегралы по формуле Ньютона- Лейбница. а) Задание 6. Найти общее решение дифференциального уравнения
удовлетворяющее начальным условиям х0=0, у0=0, Задание 7. Написать три первых члена ряда по заданному общему члену
исследовать сходимость ряда на концах интервала.
Вариант № 2. Задание 1. Найти пределы функций. а) в) д) Задание 2. Найти производные заданных функций. а) в) Задание 3. Исследовать средствами дифференциального исчисления функцию Задание 4. Найти неопределенные интегралы. а) в) Задание 5. Вычислить определенные интегралы по формуле Ньютона- Лейбница. а) Задание 6. Найти общее решение дифференциального уравнения
удовлетворяющее начальным условиям х0=p/2, у0=0. Задание 7. Написать три первых члена ряда по заданному общему члену
исследовать сходимость ряда на концах интервала.
Вариант № 3. Задание 1. Найти пределы функций. а) в) д) Задание 2. Найти производные заданных функций. а) в) Задание 3. Исследовать средствами дифференциального исчисления функцию Задание 4. Найти неопределенные интегралы. а) в) Задание 5. Вычислить определенные интегралы по формуле Ньютона- Лейбница. а) Задание 6. Найти общее решение дифференциального уравнения
удовлетворяющее начальным условиям х0=0, у0= Задание 7. Написать три первых члена ряда по заданному общему члену
исследовать сходимость ряда на концах интервала.
Вариант № 4. Задание 1. Найти пределы функций. а) в) д) Задание 2. Найти производные заданных функций. а) в) Задание 3. Исследовать средствами дифференциального исчисления функцию Задание 4. Найти неопределенные интегралы. а) в) Задание 5. Вычислить определенные интегралы по формуле Ньютона- Лейбница. а) Задание 6. Найти общее решение дифференциального уравнения
удовлетворяющее начальным условиям х0=0, у0=0. Задание 7. Написать три первых члена ряда по заданному общему члену
исследовать сходимость ряда на концах интервала.
Вариант № 5. Задание 1. Найти пределы функций. а) в) д) Задание 2. Найти производные заданных функций. а) в) Задание 3. Исследовать средствами дифференциального исчисления функцию Задание 4. Найти неопределенные интегралы. а) в) Задание 5. Вычислить определенные интегралы по формуле Ньютона- Лейбница. а) Задание 6. Найти общее решение дифференциального уравнения
удовлетворяющее начальным условиям х0=0, у0=0. Задание 7. Написать три первых члена ряда по заданному общему члену
исследовать сходимость ряда на концах интервала.
Вариант № 6. Задание 1. Найти пределы функций. а) в) д) Задание 2. Найти производные заданных функций. а) в) Задание 3. Исследовать средствами дифференциального исчисления функцию Задание 4. Найти неопределенные интегралы. а) в) Задание 5. Вычислить определенные интегралы по формуле Ньютона- Лейбница. а) Задание 6. Найти общее решение дифференциального уравнения
удовлетворяющее начальным условиям х0=0, у0=0 Задание 7. Написать три первых члена ряда по заданному общему члену
Вариант № 7. Задание 1. Найти пределы функций. а) в) д) Задание 2. Найти производные заданных функций. а) в) Задание 3. Исследовать средствами дифференциального исчисления функцию Задание 4. Найти неопределенные интегралы. а) в) Задание 5. Вычислить определенные интегралы по формуле Ньютона- Лейбница. а) Задание 6. Найти общее решение дифференциального уравнения
удовлетворяющее начальным условиям х0=0, у0=0 Задание 7. Написать три первых члена ряда по заданному общему члену
Вариант № 8. Задание 1. Найти пределы функций. а) в) д) Задание 2. Найти производные заданных функций. а) в)
Задание 3. Исследовать средствами дифференциального исчисления функцию Задание 4. Найти неопределенные интегралы. а) в) Задание 5. Вычислить определенные интегралы по формуле Ньютона- Лейбница. а) Задание 6. Найти общее решение дифференциального уравнения
удовлетворяющее начальным условиям х0=1, у0=0. Задание 7. Написать три первых члена ряда по заданному общему члену
исследовать сходимость ряда на концах интервала. Вариант № 9. Задание 1. Найти пределы функций. а) в) д) Задание 2. Найти производные заданных функций. а) в) Задание 3. Исследовать средствами дифференциального исчисления функцию Задание 4. Найти неопределенные интегралы. а) в) Задание 5. Вычислить определенные интегралы по формуле Ньютона- Лейбница. а) Задание 6. Найти общее решение дифференциального уравнения
удовлетворяющее начальным условиям х0=0, у0=1. Задание 7. Написать три первых члена ряда по заданному общему члену
исследовать сходимость ряда на концах интервала.
Вариант № 0. Задание 1. Найти пределы функций. а) в) д) Задание 2. Найти производные заданных функций. а) в) Задание 3. Исследовать средствами дифференциального исчисления функцию Задание 4. Найти неопределенные интегралы. а) в) Задание 5. Вычислить определенные интегралы по формуле Ньютона- Лейбница. а) Задание 6. Найти обшее решение дифференциального уравнения
удовлетворяющее начальным условиям х0=0, у0=0. Задание 7. Написать три первых члена ряда по заданному общему члену
исследовать сходимость ряда на концах интервала.
Вариант № 1. Задание 1. Найти пределы функций. а) в) д) Задание 2. Найти производные заданных функций. а) в) Задание 3. Исследовать средствами дифференциального исчисления функцию Задание 4. Найти неопределенные интегралы. а) в) Задание 5. Вычислить определенные интегралы по формуле Ньютона- Лейбница. а) Задание 6. Найти общее решение дифференциального уравнения
удовлетворяющее начальным условиям х0=0, у0=0, Задание 7. Написать три первых члена ряда по заданному общему члену
исследовать сходимость ряда на концах интервала.
Вариант № 2. Задание 1. Найти пределы функций. а) в) д) Задание 2. Найти производные заданных функций. а) в) Задание 3. Исследовать средствами дифференциального исчисления функцию Задание 4. Найти неопределенные интегралы. а) в) Задание 5. Вычислить определенные интегралы по формуле Ньютона- Лейбница. а) Задание 6. Найти общее решение дифференциального уравнения
удовлетворяющее начальным условиям х0=p/2, у0=0. Задание 7. Написать три первых члена ряда по заданному общему члену
исследовать сходимость ряда на концах интервала.
Вариант № 3. Задание 1. Найти пределы функций. а) в) д) Задание 2. Найти производные заданных функций. а) в) Задание 3. Исследовать средствами дифференциального исчисления функцию Задание 4. Найти неопределенные интегралы. а) в) Задание 5. Вычислить определенные интегралы по формуле Ньютона- Лейбница. а) Задание 6. Найти общее решение дифференциального уравнения
удовлетворяющее начальным условиям х0=0, у0= Задание 7. Написать три первых члена ряда по заданному общему члену
исследовать сходимость ряда на концах интервала.
Вариант № 4. Задание 1. Найти пределы функций. а) в) д) Задание 2. Найти производные заданных функций. а) в) Задание 3. Исследовать средствами дифференциального исчисления функцию Задание 4. Найти неопределенные интегралы. а) в) Задание 5. Вычислить определенные интегралы по формуле Ньютона- Лейбница. а) Задание 6. Найти общее решение дифференциального уравнения
удовлетворяющее начальным условиям х0=0, у0=0. Задание 7. Написать три первых члена ряда по заданному общему члену
исследовать сходимость ряда на концах интервала.
Вариант № 5. Задание 1. Найти пределы функций. а) в) д) Задание 2. Найти производные заданных функций. а) в) Задание 3. Исследовать средствами дифференциального исчисления функцию Задание 4. Найти неопределенные интегралы. а) в) Задание 5. Вычислить определенные интегралы по формуле Ньютона- Лейбница. а) Задание 6. Найти общее решение дифференциального уравнения
удовлетворяющее начальным условиям х0=0, у0=0. Задание 7. Написать три первых члена ряда по заданному общему члену
исследовать сходимость ряда на концах интервала.
Вариант № 6. Задание 1. Найти пределы функций. а) в) д) Задание 2. Найти производные заданных функций. а) в) Задание 3. Исследовать средствами дифференциального исчисления функцию Задание 4. Найти неопределенные интегралы. а) в) Задание 5. Вычислить определенные интегралы по формуле Ньютона- Лейбница. а) Задание 6. Найти общее решение дифференциального уравнения
удовлетворяющее начальным условиям х0=0, у0=0 Задание 7. Написать три первых члена ряда по заданному общему члену
Вариант № 7. Задание 1. Найти пределы функций. а) в) д) Задание 2. Найти производные заданных функций. а) в) Задание 3. Исследовать средствами дифференциального исчисления функцию Задание 4. Найти неопределенные интегралы. а) в) Задание 5. Вычислить определенные интегралы по формуле Ньютона- Лейбница. а) Задание 6. Найти общее решение дифференциального уравнения
удовлетворяющее начальным условиям х0=0, у0=0 Задание 7. Написать три первых члена ряда по заданному общему члену
Вариант № 8. Задание 1. Найти пределы функций. а) в) д) Задание 2. Найти производные заданных функций. а) в)
Задание 3. Исследовать средствами дифференциального исчисления функцию Задание 4. Найти неопределенные интегралы. а) в) Задание 5. Вычислить определенные интегралы по формуле Ньютона- Лейбница. а) Задание 6. Найти общее решение дифференциального уравнения
удовлетворяющее начальным условиям х0=1, у0=0. Задание 7. Написать три первых члена ряда по заданному общему члену
исследовать сходимость ряда на концах интервала. Вариант № 9. Задание 1. Найти пределы функций. а) в)
|

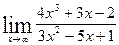 ; б)
; б)  ;
; ; г)
; г)  ;
; .
. ; б)
; б)  ;
; ; г)
; г)  .
.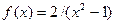 и построить ее график.
и построить ее график. ; б)
; б) 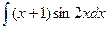 ;
; ; г)
; г) 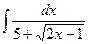 .
. ; б)
; б)  .
.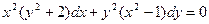 и частное решение,
и частное решение, , определить интервал сходимости ряда и
, определить интервал сходимости ряда и ; б)
; б)  ;
; ; г)
; г)  ;
; .
. ; б)
; б)  ;
; ; г)
; г)  .
. и построить ее график.
и построить ее график.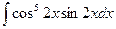 ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  .
.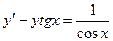 и частное решение, удовлетворяющее начальным условиям х0=0, у0=0.
и частное решение, удовлетворяющее начальным условиям х0=0, у0=0. .
. , определить интервал сходимости ряда и
, определить интервал сходимости ряда и ; б)
; б)  ;
; ; г)
; г)  ;
; .
.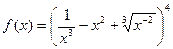 ; б)
; б)  ;
; ; г)
; г)  .
. и построить ее график.
и построить ее график. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  .
.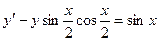 и частное решение,
и частное решение,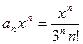 , определить интервал сходимости ряда и
, определить интервал сходимости ряда и ; б)
; б) 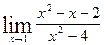 ;
; ; г)
; г)  ;
; .
. ; б)
; б)  ;
; ; г)
; г) 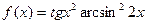 .
. и построить ее график.
и построить ее график.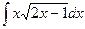 ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б) 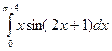 .
.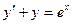 и частное решение,
и частное решение, .
. , определить интервал сходимости ряда и
, определить интервал сходимости ряда и ; б)
; б)  ;
; ; г)
; г)  ;
; .
.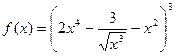 ; б)
; б)  ;
; ; г)
; г)  .
. и построить ее график.
и построить ее график. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  .
. и частное решение,
и частное решение, , определить интервал сходимости ряда и
, определить интервал сходимости ряда и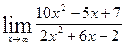 ; б)
; б) 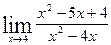 ;
; ; г)
; г)  ;
; .
. ; б)
; б)  ;
; ; г)
; г) 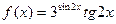 .
. и построить ее график.
и построить ее график. ; б)
; б) 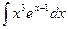 ;
; ; г)
; г)  .
.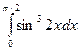 ; б)
; б) 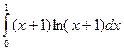 .
. и частное решение,
и частное решение, , определить интервал сходимости ряда и
, определить интервал сходимости ряда и ; б)
; б)  ;
; ; г)
; г)  ;
; .
. ; б)
; б)  ;
; ; г)
; г)  .
.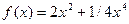 и построить ее график.
и построить ее график. ; б)
; б)  ;
; ; г)
; г)  .
.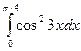 ; б)
; б)  .
. и частное решение,
и частное решение,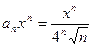 , определить интервал сходимости ряда и исследовать сходимость ряда на концах интервала.
, определить интервал сходимости ряда и исследовать сходимость ряда на концах интервала. ; б)
; б)  ;
;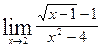 ; г)
; г) 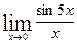 ;
; .
. ; б)
; б)  ;
;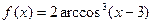 ; г)
; г)  .
. и построить ее график.
и построить ее график. ; б)
; б) 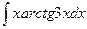 ;
; ; г)
; г) 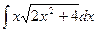 .
. ; б)
; б)  .
.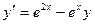 и частное решение, удовлетворяющее начальным условиям х0=0, у0=0.
и частное решение, удовлетворяющее начальным условиям х0=0, у0=0.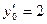 .
. , определить интервал сходимости ряда и исследовать сходимость ряда на концах интервала.
, определить интервал сходимости ряда и исследовать сходимость ряда на концах интервала. ; б)
; б)  ;
;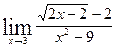 ; г)
; г) 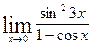 ;
; .
. ; б)
; б)  ;
; ; г))
; г))  .
. и построить ее график.
и построить ее график.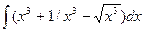 ; б)
; б) 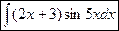 ;
; ; г)
; г)  .
. ; б)
; б) 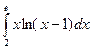 .
. и частное решение,
и частное решение, , определить интервал сходимости ряда и
, определить интервал сходимости ряда и ; б)
; б) 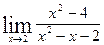 ;
; ; г)
; г)  ;
; .
. ; б)
; б)  ;
; ; г)
; г)  .
. и построить ее график.
и построить ее график.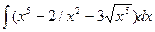 ; б)
; б)  ;
; ; г)
; г)  .
. .
.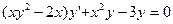 и частное решение,
и частное решение, , определить интервал сходимости ряда и
, определить интервал сходимости ряда и ; б)
; б)  ;
; ; г)
; г)  ;
; .
. ; б)
; б)  ;
; ; г)
; г)  .
. и построить ее график.
и построить ее график. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  .
. и частное решение,
и частное решение, , определить интервал сходимости ряда и
, определить интервал сходимости ряда и ; б)
; б)  ;
; ; г)
; г)  ;
; .
. ; б)
; б)  ;
; ; г)
; г)  .
. и построить ее график.
и построить ее график. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  .
. и частное решение, удовлетворяющее начальным условиям х0=0, у0=0.
и частное решение, удовлетворяющее начальным условиям х0=0, у0=0. .
. , определить интервал сходимости ряда и
, определить интервал сходимости ряда и ; б)
; б)  ;
; ; г)
; г)  ;
; .
. ; б)
; б)  ;
; ; г)
; г)  .
. и построить ее график.
и построить ее график. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  .
. и частное решение,
и частное решение, , определить интервал сходимости ряда и
, определить интервал сходимости ряда и ; б)
; б)  ;
; ; г)
; г)  ;
; .
. ; б)
; б)  ;
; ; г)
; г)  .
. и построить ее график.
и построить ее график. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  .
. и частное решение,
и частное решение, .
. , определить интервал сходимости ряда и
, определить интервал сходимости ряда и ; б)
; б)  ;
; ; г)
; г)  ;
; .
. ; б)
; б)  ;
; ; г)
; г)  .
. и построить ее график.
и построить ее график. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  .
. и частное решение,
и частное решение, , определить интервал сходимости ряда и
, определить интервал сходимости ряда и ; б)
; б)  ;
; ; г)
; г)  ;
; .
. ; б)
; б)  ;
; ; г)
; г)  .
. и построить ее график.
и построить ее график. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  .
. и частное решение,
и частное решение, , определить интервал сходимости ряда и
, определить интервал сходимости ряда и ; б)
; б)  ;
; ; г)
; г)  ;
; .
. ; б)
; б)  ;
; ; г)
; г)  .
. и построить ее график.
и построить ее график. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  .
. и частное решение,
и частное решение, , определить интервал сходимости ряда и исследовать сходимость ряда на концах интервала.
, определить интервал сходимости ряда и исследовать сходимость ряда на концах интервала. ; б)
; б)  ;
; ; г)
; г)  ;
; .
. ; б)
; б)  ;
; ; г)
; г)  .
. и построить ее график.
и построить ее график. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  .
. и частное решение, удовлетворяющее начальным условиям х0=0, у0=0.
и частное решение, удовлетворяющее начальным условиям х0=0, у0=0. .
. , определить интервал сходимости ряда и исследовать сходимость ряда на концах интервала.
, определить интервал сходимости ряда и исследовать сходимость ряда на концах интервала. ; б)
; б)  ;
; ; г)
; г)  ;
; .
. ; б)
; б)  ;
; ; г))
; г))  .
. и построить ее график.
и построить ее график. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  .
. и частное решение,
и частное решение, , определить интервал сходимости ряда и
, определить интервал сходимости ряда и ; б)
; б)  ;
; ; г)
; г) 


